How to Cite
Share
Copyright (c) 2023 Frederik Alexander Falk, Rasmus Bødker Madsen
This work is licensed under a Creative Commons Attribution 4.0 International License.
Abstract
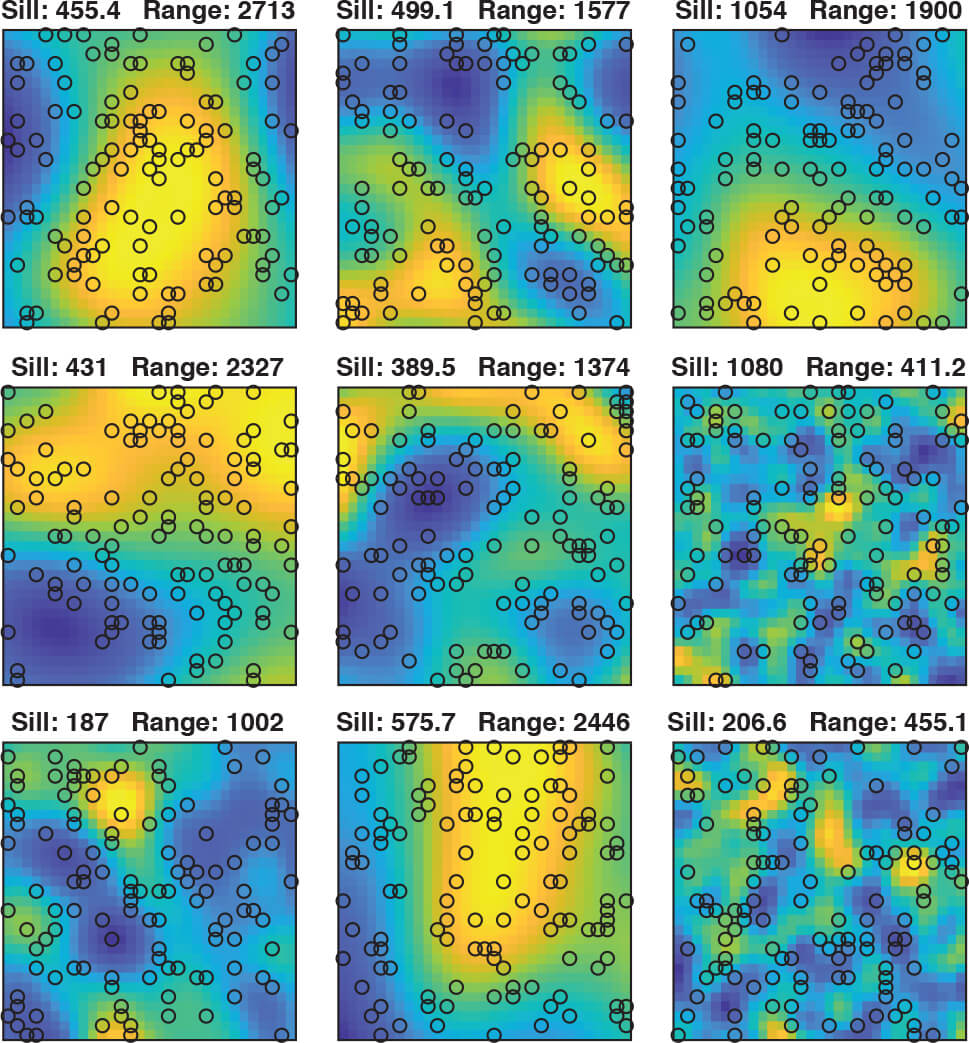
Estimating a covariance model for kriging purposes is traditionally done using semivariogram analyses, where an empirical semivariogram is calculated, and a chosen semivariogram model, usually defined by a sill and a range, is fitted. We demonstrate that a convolutional neural network can estimate such a semivariogram model with comparable accuracy and precision by training it to recognise the relationship between realisations of Gaussian random fields and the sill and range values that define it, for a Gaussian type semivariance model. We do this by training the network with synthetic data consisting of many such realisations with the sill and range as the target variables. Because training takes time, the method is best suited for cases where many models need to be estimated since the actual estimation itself is about 70 times faster with the neural network than with the traditional approach. We demonstrate the viability of the method in three ways: (1) we test the model’s performance on the validation data, (2) we do a test where we compare the model to the traditional approach and (3) we show an example of an actual application of the method using the Danish national hydrostratigraphic model.
How to Cite
Share
Copyright (c) 2023 Frederik Alexander Falk, Rasmus Bødker Madsen
This work is licensed under a Creative Commons Attribution 4.0 International License.
Downloads
An annual collection of articles submitted to GEUS Bulletin and published throughout 2023. Published online only. This issue is open until the end of 2023.
Cover photo: satellite image is from the European Space Agency’s Copernicus Sentinel data 2023, as featured in Karlsson et al. 2023: A data set of monthly [...]
References
- Boisvert, J.B. & Deutsch, C.V. 2011: Programs for kriging and sequential Gaussian simulation with locally varying anisotropy using non-Euclidean distances. Computers & Geosciences 37(4), 495–510. https://doi.org/10.1016/j.cageo.2010.03.021
- Boisvert, J.B., Manchuk, J. & Deutsch, C.V. 2009: Kriging in the presence of locally varying anisotropy using non-Euclidean distances. Mathematical Geosciences 41, 585–601. https://doi.org/10.1007/s11004-009-9229-1
- Bongajum, E.L., Boisvert, J. & Sacchi, M.D. 2013: Bayesian linearized seismic inversion with locally varying spatial anisotropy. Journal of Applied Geophysics 88, 31–41. https://doi.org/10.1016/j.jappgeo.2012.10.001
- Cressie, N.A.C. 1993: Statistics for spatial data. New York: Wiley.
- Hansen et al. 2013: SIPPI: A MATLAB toolbox for sampling the solution to inverse problems with complex prior information: Part 1 – Methodology. Computational Geoscience 52, 470–480. https://doi.org/10.1016/j.cageo.2012.09.004
- Higdon D., Swall, J., & Kern, J. 1999: Non-stationary spatial modeling. In: Bernado, J.M. et al. (eds). Bayesian Statistics (6 ed.). 761–768. Oxford: Oxford University Press.
- Hornik, K. 1991: Approximation capabilities of multilayer feedforward networks. Neural Networks 4(2), 251–257. https://doi.org/10.1016/0893-6080(91)90009-T
- Iandola, F.N., Moskewicz, M.W., Ashraf, K., Han, S., Dally, W.J. & Keutzer, K. 2016: SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <1MB model size. ArXiv, abs/1602.07360. https://doi.org/10.48550/arXiv.1602.07360
- Jo, H. & Pyrcz, M.J. 2022: Automatic semivariogram modeling by convolutional neural network. Mathematical Geosciences 54(1), 177–205. https://doi.org/10.1007/s11004-021-09962-w
- Kohonen, T. 1991: Self-organising maps: ophmization approaches. In: Kohonen, T., et al. (eds): Artificial Neural Networks. Pp. 981–990. Amsterdam: North-Holland. https://doi.org/10.1016/B978-0-444-89178-5.50003-8
- Li, Y., Baorong, Z., Xiaohong, X. & Zijun, L. 2022: Application of a semivariogram based on a deep neural network to ordinary kriging interpolation of elevation data. PLoS One 17(4), e0266942. https://doi.org/10.1371/journal.pone.0266942
- Madsen, R.B., Hansen, T.M. & Omre, H. 2020: Estimation of a non-stationary prior covariance from seismic data. Geophysical Prospecting 68(2), 393–410. https://doi.org/10.1111/1365-2478.12848
- Madsen, R.B., Høyer, A.S., Andersen, L.T., Møller, I. & Hansen, T.M. 2022: Geology-driven modelling: A new probabilistic approach for incorporating uncertain geological interpretations in 3D geological modelling. Engineering Geology 309, 106833. https://doi.org/10.1016/j.enggeo.2022.106833
- Mardia, K.V. 1990: Maximum likelihood estimation for spatial models in Spatial statistics: Past, present, and future. 203–253. https://doi.org/10.1068/a270615
- Matheron, G. 1963: Principles of geostatistics. Economic Geology 58(8), 1246–1266. https://doi.org/10.2113/gsecongeo.58.8.1246
- Pereira, Â. et al. 2023: Updating local anisotropies with template matching during geostatistical seismic inversion. Mathematical Geosciences 55(4), 497–519, https://doi.org/10.1007/s11004-023-10051-3
- Stisen, S., Ondracek, M., Troldborg, L., Schneider, R.J.M. & Til, M.J.V. 2020: National Vandressource Model. Modelopstilling og kalibrering af DK-model 2019. Danmarks og Grønlands Geologiske Undersøgelse Rapport 2019/31, 23–27, https://doi.org/10.22008/gpub/32631
- Zhou, L., Hongming, P., Wang, F., Zhiqiang, H. & Wang, L. 2017: The expressive power of neural networks: A view from the width. In: Guyon, I. et al. (eds.) Advances in Neural Information Processing Systems 30, 7–8. New York: Curran Associates Inc. https://proceedings.neurips.cc/paper_files/paper/2017/file/32cbf687880eb1674a07bf717761dd3a-Paper.pdf (accessed October 2023)
