METHOD ARTICLE

Machine learning-based estimation and clustering of statistics within stratigraphic models as exemplified in Denmark

Frederik Alexander Falk^*1, Rasmus Bødker Madsen²

¹Department of Geoscience, Aarhus University, Aarhus, Denmark; ²Department of Near Surface Land and Marine Geology, Geological Survey of Denmark and Greenland (GEUS), Aarhus, Denmark

Abstract

Estimating a covariance model for kriging purposes is traditionally done using semivariogram analyses, where an empirical semivariogram is calculated, and a chosen semivariogram model, usually defined by a sill and a range, is fitted. We demonstrate that a convolutional neural network can estimate such a semivariogram model with comparable accuracy and precision by training it to recognise the relationship between realisations of Gaussian random fields and the sill and range values that define it, for a Gaussian type semivariance model. We do this by training the network with synthetic data consisting of many such realisations with the sill and range as the target variables. Because training takes time, the method is best suited for cases where many models need to be estimated since the actual estimation itself is about 70 times faster with the neural network than with the traditional approach. We demonstrate the viability of the method in three ways: (1) we test the model’s performance on the validation data, (2) we do a test where we compare the model to the traditional approach and (3) we show an example of an actual application of the method using the Danish national hydrostratigraphic model.

Tabular abstract

Geographical coverage	Fyn, Denmark
Temporal coverage	N/A
Subject(s) covered	Geophysics, Computational geoscience, informatics and remote sensing
Method type	A new machine learning-based method for estimating locally optimised semivariogram parameters for grid cells in stratigraphic models followed by clustering for the introduction of the assumption of local stationarity.
Method name	Machine learning-based semivariogram model estimation and clustering
Instruments and equipment used	Equipment Used: - A sufficiently effective computer - MATLAB® software license      • Machine Learning Toolbox for MATLAB      • SIPPI Geostatistics Toolbox for MATLAB      • mGstat Geostatistics Toolbox for MATLAB
Related publications	None
Potential application(s) for this method	This method may be used to infer a statistical model from one stratigraphic model, which is useful for uncertainty quantification. The method is also useful for very fast semivariogram modelling whenever the advantage of doing so outweighs the time it takes to train the model.

 

 

Introduction

The properties of the subsurface are highly non-stationary, that is, they vary significantly depending on the location. Consequently, in statistical descriptions of the subsurface, there is a need for mapping non-stationarity in the statistical properties and for practical purposes also defining regions wherein local stationarity can be assumed (Boisvert et al. 2009).

Estimating the statistical properties of spatially distributed data is conventionally done through semivariogram analysis, where an experimental semivariogram is calculated as half the average squared difference between points separated by some distance, h (Matheron 1963). A model is fitted to the semivariogram, which is typically defined by two parameters – a range and a sill, and oftentimes also a nugget effect (Cressie 1993). Alternatively, it is possible to estimate a semivariogram model by determining the maximum-likelihood combination of sill and range given the type of model. The likelihood for a semivariogram model is obtained by populating a covariance matrix using the model and taking the probability density of the corresponding multivariate normal distribution at the point defined by the data (Mardia 1990). Fitting a semivariogram and estimating the maximum-likelihood model share the drawbacks of being computationally intensive when many models need to be estimated.

We propose a new method of estimating the sill and range given a set of spatially distributed data using machine learning (ML), specifically a convolutional neural network (CNN), which is more efficient when estimating many models. A CNN is trained to recognise the approximate mapping from a realisation of a Gaussian random field to the semivariogram model that defines its probability density function. This mapping is not bijective in nature, and as such, it is not a function. However, the network should still be able to approximate a function that resembles the mapping to some degree.

The idea of using a CNN for semivariogram modelling has been proposed before. One study used separate networks for interpolation and parameter estimation (Jo & Pyrcz 2022). Others skipped parameterised models and directly estimated semivariograms for kriging (Li et al. 2022). We have chosen to focus on estimating Gaussian model parameters using one network to infer their spatial distribution within large models and make the process computationally feasible. We test the method on the Danish national hydrostratigraphic model (DK-model; Stisen et al. 2020). We show that where local stationarity may be assumed, we can define regions within the hydrostratigraphic model with reasonable accuracy by clustering the models.

Required resources

The required resources are as follows:

• A sufficiently effective computer
• MATLAB® 2022b or newer – older versions have not been tested for this method. Also, the Machine Learning Toolbox for MATLAB, SIPPI Geostatistics Toolbox for MATLAB and the mGstat Geostatistics Toolbox for MATLAB
• Data in the form of scattered points with a value for each point, either with irregular spacing or as a regular grid

Methodological protocols

We use the CNN’s ability to efficiently detect structural patterns in an image, and as such, it needs a regular grid as input. We consider two cases: one where data constitute a full grid and one with scattered point data interpolated to produce a grid. For the network input, we chose the grid size 31 × 31 cells with a cell size of 100 m, and we adapted the neural Network (NN) architecture from the SqueezeNet convolutional neural network (Iandola et al. 2016), which is a native architecture in the MATLAB Machine Learning Toolbox.

Producing training, validation and test data

We produced synthetic data for the NN using the SIPPI toolbox in MATLAB (Hansen et al. 2013) by taking 150 000 values for sill and range from uniform distributions, such that the sills vary between 0 m² and 1100 m², and the ranges vary between 100 m and 3000 m.

We then simulate a realisation from each of the Gaussian random fields that have the Gaussian semivariance functions defined by the pairs of sill and range values. Each realisation is on the 31 × 31 grid with a cell size of 100 m.

To include some component of noise, we simulated and added one more realisation to each existing realisation, with the same effective range, and the sill being random between 0 m² and the sill of the original realisation itself. Figure 1 shows nine examples of the synthetic data.

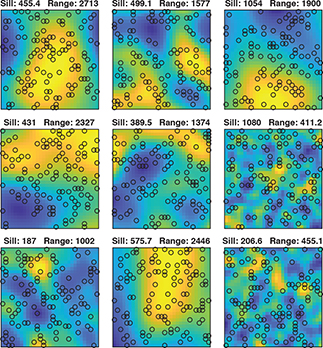
Fig. 1 Synthetic training data produced using Gaussian semivariance models with random sill and range, with a component of noise. The circles show 120 randomly drawn points from each realisation. Shading: smallest values are shown in blue and largest values are shown in yellow, with in-between values shown in green.

The synthetic data are saved both as full grids and sets of 120 points with an x-coordinate, a y-coordinate and a z-coordinate. We split the synthetic data into a training set, consisting of 90% of the data, as well as a validation and a training set, each being 5% of the data.

Training the network

The network is trained with the ‘Adam’ optimisation algorithm, and the loss function is represented by the mean squared error. We used a constant learning rate of 0.0005 and a batch size of 1000 whilst training the model for 100 epochs. The total training time for the network is about 1 h. We also found that model training time could be reduced to only a few minutes if we included the fast Fourier transform as a second image input channel. Ultimately, we chose not to do this because that requires us to calculate the Fourier transform of the data input every time we want to use the model. This is a disadvantage because it slows down the prediction process, which becomes an issue when applied to very large models. The Fourier transform could be useful if training data are scarce, which could be the case with non-synthetic training data. At this point, the network is ready to use, and only requires a 31 × 31 grid input. The training can also be done with point data. However, as the CNN is based on image convolution, one should choose an interpolation method and convert the point data to a grid.

Validation

We demonstrate the advantage of using ML for the estimation of the semivariogram model with a synthetic example, where the method is compared to the classic method of fitting an experimental semivariogram. We then demonstrate the advantage of applying the method given an actual use case.

The 5% of the data, which we set aside for validation, are fed to the network and serve as an initial validation test. The size of the validation set is 7500 data points. Figure 2 shows the distribution of true to predicted values for the range and sill for the validation data set. A common way to estimate the sill is to simply take the sample variance of the scattered points, which is also shown in Fig. 2.

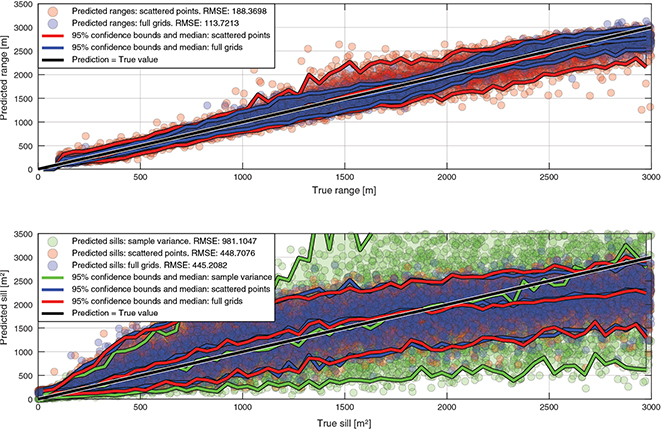
Fig. 2 The panels show the precision and accuracy of the ML model in predicting range and sill. Red dots show values predicted using the scattered points and blue dots using full grids, and green dots show the estimation of sill using the sample variance from the 120 scattered points. The black trend lines indicate where points are in exact agreement with the true values. The colour-shaded regions highlight the interval within which 95% of predictions are made, bounded by the 2.5 percentile (lowermost coloured lines), 50 percentile (median; middle coloured lines) and 97.5 percentile (uppermost coloured lines).

The predicted range values are very close to the true values for both scattered data and full grids. The predictions using full grids are a little more accurate, which we expected since the scattered points are drawn from the full grids and thus contain less information. The predictions for the sill are equally precise between the two cases and even share the same apparent biases. For example, at sill values of 500 to 1500, the ML model over-estimates, whilst it underestimates for sill values above 2000. Although we did not use bias description, it is possible by fitting a suitable polynomial function between prediction and actual values. Correcting the estimates to account for bias is then straightforward. Alternatively, it is reasonable to assume that improvements in the NN itself could eliminate the bias. The variance estimate is less precise but has no bias.

Validation on synthetic data

We take a set of 1000 new synthetic realisations of size 31 × 31, each with 120 randomly drawn points, and we use these points to:

1. Perform a traditional semivariogram analysis with the following steps:
   1. Calculate an empirical semivariogram from the points.
   2. Fit a Gaussian semivariance model to the semivariogram using a weighted least-squares approach, where points closer to the origin have greater weight.
2. Predict the sill and range directly with our CNN with the following steps:
   1. Interpolate the 120 points onto the entire grid.
   2. Pass the interpolated grid through the CNN.

We then compare the accuracy of the estimates with these two methods as well as the time it takes to complete. The result of the accuracy comparison is shown in Fig. 3 for eight different realisations. Depending on the specific realisation, it varies whether the fitted model (black line) or CNN (blue line) is better at resolving the true model (red line). Across all 1000 realisations, we see that the CNN is slightly better at approximating large values for the range than the traditional approach, whereas the traditional method is slightly better at low values. In general, both methods have similar performance.

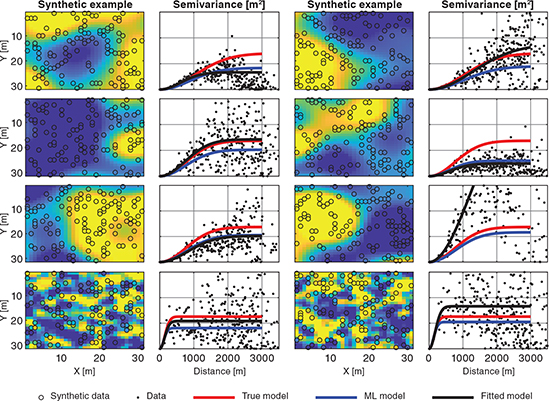
Fig. 3 Synthetic examples: 8 realisations are shown – each of their own Gaussian semivariogram model with some component of noise. The semivariance models show a high level of accuracy for the traditional fitting approach as well as the ML approach.

However, the time that the methods need to reach the predictions is not the same. During the test, we recorded the time spent for each approach and calculated the average time spent per model. The CNN approach based on existing 31 × 31 grids was able to estimate 130 semivariogram models per second, whilst for scattered data, 111 models could be estimated per second. Meanwhile, the traditional semivariogram analysis, where a model is fitted to an experimental semivariogram, could only estimate 1.72 models per second. Of course, these numbers depend on the computational resources available, but the important point is the relative difference in computation time between the methods.

The time consumption of the ML approach is only slightly larger when interpolating point data, suggesting that the CNN consumes most of the time and not the interpolation itself. Meanwhile, the traditional approach of fitting takes about 60 times more computation time.

The time consumption varies quite a bit for the traditional semivariogram analysis approach, depending on the number of data points used. By using only 60 points, it may complete as many as 30 models per second; however, this is still about one-fourth of the speed of the CNN and with a significant loss of accuracy. Furthermore, the CNN may also be optimised to become more efficient.

Validation by application of the method

Besides the validation on synthetic data, we also validate our method by demonstrating how it can be used to solve a real problem of obtaining non-stationary statistical properties. When dealing with models with non-stationary statistics, such as very large models like the DK-model (Stisen et al. 2020), using a single semivariogram for kriging does not usually produce realistic geological structures. In our validation example, we employ the ML approach to estimate local values for the range and the sill and then use a clustering algorithm to divide the model into local regions with similar statistical properties. The algorithm is a type of unsupervised classification algorithm known as the Kohonen self-organising map (Kohonen 1991), which is featured as a built-in function in MATLAB. With this approach, the ML algorithm enables kriging with a locally optimised semivariogram model, which should be better at handling non-stationary models than approaches with a fixed semivariogram model.

For the validation example, we employ this approach to the first layer in the hydrostratigrahic model on the Danish island of Fyn, covering roughly 3100 km². The sample variance is used to estimate the sill in this example because an unbiased estimation is prioritised over a precise estimation for the purpose of clustering. As such, the example focuses on the predicted ranges and the final clustering. The top left panel in Fig. 3 shows the ranges predicted with a 31 × 31 sliding window, whilst the top right panel shows the subsequent clustering result.

Figure 4 illustrates how the ML algorithm identifies areas of low range where the layer has more high-frequency variation and areas of high range where the layer resembles more of a smooth curve. Of course, this should be seen in the context of the chosen window size, which is about 3100 m, and larger ranges than this cannot be resolved. This limitation should not pose a problem since any subsequent kriging and simulation will be modelling the residual around the sliding mean from the layer using the same window.

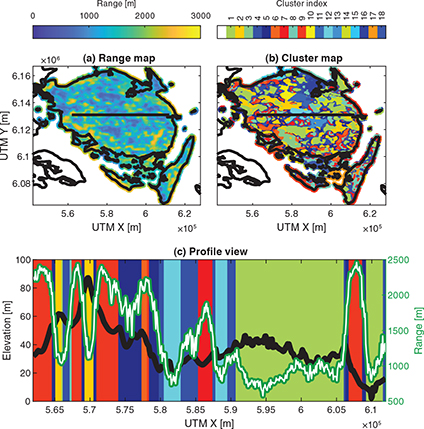
Fig. 4 Method results of a layer covering the Danish island of Fyn. (a) Predicted ranges. (b) Ranges clustered into regions. (c) Layer elevation across the black profile shown in (a) and (b) and the predicted ranges (green/white line) across the same profile. The colour scale in (c) matches the colour scale in (b), showing where individual clusters are located.

The example layer shown here contains 497 369 individual grid cells, which means that the machine learning algorithm can complete the semivariance model estimation in about 1 h and 15 min, given a computation rate of 111 models per second. Meanwhile, the traditional semivariogram analysis takes about 80 h to do the same, given a rate of 1.72 models per second.

Discussion and outlook

In a subsurface model with a large spatial extent, the assumption of stationarity in the subsurface properties breaks down. To do proper geostatistical modelling in such a case, non-stationarity must be considered (Higdon et al. 2022). Non-stationarity can be modelled by introducing locally varying anisotropy (e.g. Boisvert & Deutsch 2011; Bongajum et al. 2013; Pereira et al. 2023), but these methods can be computationally challenging for large models. Thus, practical tools needed for estimating the non-stationarity are currently sparse and not easily deployed for practitioners (Madsen et al. 2020). Here, we briefly presented a computationally efficient ML-based method that can infer Gaussian properties from a stratigraphic layer model, adding a new tool to the geostatistician’s toolbox to solve issues of non-stationarity.

During testing, several different ML approaches were tried, including regression trees, random forest and a classical NN, but the deployment and adoption of a CNN were the most successful. It is known that Neural Networks in general are universal approximators that can approximate any continuous Lebesgue integrable function. This was proven for networks with a fixed number of hidden layers and an arbitrary number of neurons, also known as the arbitrary width case (Hornik 1991). Recently, it was also proven for ReLU NNs with a fixed number of neurons (fixed width) and an arbitrary number of hidden layers, also known as the arbitrary depth case (Zhou et al. 2017). In the presented use-case, the CNN probably produced better estimates compared to the other ML approaches because the convolution of different layers makes the CNN better at analysing the spatial information in the training data. With the rapid development in ML algorithms, the CNN might soon be outperformed; however, the methodology of training the ML model to recognise Gaussian covariances from point data does not change but can only improve its precision with new algorithms. This presents an improvement over, for example, a traditional semivariogram analysis, the performance of which comes with a trade-off between the ability to accurately predict shorter versus longer ranges. This trade-off occurs due to the constraints imposed by the weights on the experimental variogram at different range intervals.

The NN architecture used from SqueezeNet (Iandola et al. 2016) is ideal for obtaining good predictions by training the model using a conventional gradient descent algorithm with a sufficiently large training data set. We found that optimal results are obtained when training on at least 100 000 independent realisations, with performance severely decreasing when training on less than 10 000 realisations.

The presented approach also has the major advantage of having limitless training data available, although a reasonable amount of training data should be chosen for computational feasibility. The network can also be trained to a larger grid than the 31 × 31 grid used here, giving a lot of flexibility for the specific model for which inference is needed. The 31 × 31 grid posed some issues for estimating ranges over a certain length. This limitation to the method can be remedied by increasing the grid size, but at the cost of increasing computation time during training of the CNN. To determine the right size of the grid in a practical case, we suggest training two preliminary networks with a small grid and a slightly larger grid. If predictions with these two networks deviate significantly when applied on real data, the grid size must be increased to accommodate all possible ranges. The process can be repeated iteratively until the same range interval is predicted for both networks, indicating a reasonable minimum grid size. Using this strategy for the DK-model, a 31 × 31 grid was deemed suitable as showcased.

Our results in the synthetic case suggest that the deployed CNN has the same accuracy as a traditional automatic semivariogram fitting, but with a substantial improvement in speed, which now makes it feasible to analyse large grids within a reasonable amount of computation time as showcased in the final validation example to account for non-stationarity. The subsequent clustering also makes it possible to define regions with comparable statistics in the stratigraphical model. For further application of the estimated statistical models, one could infer the local statistics from the sill and range estimates within each cluster and use these for, for example, localised geostatistical estimation (kriging) or simulation of each cluster instead of using a stationary model as done in Madsen et al. (2022) for a hydrostratigraphic model.

Acknowledgements

The authors would like to acknowledge the Geological Survey of Denmark and Greenland (GEUS) for providing funding for writing the manuscript as the method development was carried out in a consultancy project without funding for scientific publication.

Additional information

Author contributions

FAF: Methodology, Software, Investigation, Writing – Original draft preparation

RBM: Conceptualisation, Methodology, Writing – Reviewing and Editing

Additional files

None provided

References

Boisvert, J.B. & Deutsch, C.V. 2011: Programs for kriging and sequential Gaussian simulation with locally varying anisotropy using non-Euclidean distances. Computers & Geosciences 37(4), 495–510. https://doi.org/10.1016/j.cageo.2010.03.021

Boisvert, J.B., Manchuk, J. & Deutsch, C.V. 2009: Kriging in the presence of locally varying anisotropy using non-Euclidean distances. Mathematical Geosciences 41, 585–601. https://doi.org/10.1007/s11004-009-9229-1

Bongajum, E.L., Boisvert, J. & Sacchi, M.D. 2013: Bayesian linearized seismic inversion with locally varying spatial anisotropy. Journal of Applied Geophysics 88, 31–41. https://doi.org/10.1016/j.jappgeo.2012.10.001

Cressie, N.A.C. 1993: Statistics for spatial data. New York: Wiley.

Hansen et al. 2013: SIPPI: A MATLAB toolbox for sampling the solution to inverse problems with complex prior information: Part 1 – Methodology. Computational Geoscience 52, 470–480. https://doi.org/10.1016/j.cageo.2012.09.004

Higdon D., Swall, J., & Kern, J. 1999: Non-stationary spatial modeling. In: Bernado, J.M. et al. (eds). Bayesian Statistics (6 ed.). 761–768. Oxford: Oxford University Press.

Hornik, K. 1991: Approximation capabilities of multilayer feedforward networks. Neural Networks 4(2), 251–257. https://doi.org/10.1016/0893-6080(91)90009-T

Iandola, F.N., Moskewicz, M.W., Ashraf, K., Han, S., Dally, W.J. & Keutzer, K. 2016: SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <1MB model size. ArXiv, abs/1602.07360. https://doi.org/10.48550/arXiv.1602.07360

Jo, H. & Pyrcz, M.J. 2022: Automatic semivariogram modeling by convolutional neural network. Mathematical Geosciences 54(1), 177–205. https://doi.org/10.1007/s11004-021-09962-w

Kohonen, T. 1991: Self-organising maps: ophmization approaches. In: Kohonen, T., et al. (eds): Artificial Neural Networks. Pp. 981–990. Amsterdam: North-Holland. https://doi.org/10.1016/B978-0-444-89178-5.50003-8

Li, Y., Baorong, Z., Xiaohong, X. & Zijun, L. 2022: Application of a semivariogram based on a deep neural network to ordinary kriging interpolation of elevation data. PLoS One 17(4), e0266942. https://doi.org/10.1371/journal.pone.0266942

Madsen, R.B., Hansen, T.M. & Omre, H. 2020: Estimation of a non-stationary prior covariance from seismic data. Geophysical Prospecting 68(2), 393–410. https://doi.org/10.1111/1365-2478.12848

Madsen, R.B., Høyer, A.S., Andersen, L.T., Møller, I. & Hansen, T.M. 2022: Geology-driven modelling: A new probabilistic approach for incorporating uncertain geological interpretations in 3D geological modelling. Engineering Geology 309, 106833. https://doi.org/10.1016/j.enggeo.2022.106833

Mardia, K.V. 1990: Maximum likelihood estimation for spatial models in Spatial statistics: Past, present, and future. 203–253. https://doi.org/10.1068/a270615

Matheron, G. 1963: Principles of geostatistics. Economic Geology 58(8), 1246–1266. https://doi.org/10.2113/gsecongeo.58.8.1246

Pereira, Â. et al. 2023: Updating local anisotropies with template matching during geostatistical seismic inversion. Mathematical Geosciences 55(4), 497–519, https://doi.org/10.1007/s11004-023-10051-3

Stisen, S., Ondracek, M., Troldborg, L., Schneider, R.J.M. & Til, M.J.V. 2020: National Vandressource Model. Modelopstilling og kalibrering af DK-model 2019. Danmarks og Grønlands Geologiske Undersøgelse Rapport 2019/31, 23–27, https://doi.org/10.22008/gpub/32631

Zhou, L., Hongming, P., Wang, F., Zhiqiang, H. & Wang, L. 2017: The expressive power of neural networks: A view from the width. In: Guyon, I. et al. (eds.) Advances in Neural Information Processing Systems 30, 7–8. New York: Curran Associates Inc. https://proceedings.neurips.cc/paper_files/paper/2017/file/32cbf687880eb1674a07bf717761dd3a-Paper.pdf (accessed October 2023)