DATA ARTICLE | SHORT

A data set of monthly freshwater fluxes from the Greenland ice sheet’s marine-terminating glaciers on a glacier–basin scale 2010–2020

Nanna B. Karlsson^*1, Kenneth D. Mankoff^1,2,3, Anne M. Solgaard¹, Signe H. Larsen¹, Penelope R. How¹, Robert S. Fausto¹, Louise S. Sørensen⁴

¹Geological Survey of Denmark and Greenland (GEUS), Copenhagen, Denmark. ²Autonomic Integra LLC, New York, NY, USA. ³NASA Goddard Institute for Space Studies, New York, NY, USA. ⁴DTU Space – National Space Institute, Technical University of Denmark, Kgs. Lyngby, Denmark

 

 

Abstract

The loss of mass from the Greenland ice sheet causes an increasing influx of freshwater to the Greenlandic fjords and the oceans. Freshwater fluxes from marine-terminating glaciers are important to understand fjord circulation and ecosystem dynamics. Here, we present a data set constructed by reformulating existing products into a shared temporal and spatial framework. We combine three publicly available data sets of solid-ice discharge (iceberg), liquid-surface runoff (runoff) and basal melt to present a cohesive overview of the flow of freshwater from marine-terminating glaciers to the Greenlandic fjords. We also calculate glacier drainage basins and compare our findings to previous studies showing that drainage-basin sizes may vary considerably depending on how they were reconstructed. The data set will be a valuable asset to oceanographic, glaciological and marine biological research activities.

Tabular abstract

Geographical coverage	Greenland, ice-sheet margins
Temporal coverage	2010–2020 (inclusive); monthly resolution
Subject(s)	Cryosphere, Oceanography, Atmosphere and Climate
Data format(s)	Modelled and reformatted data as CSV files are available here: https://doi.org/10.22008/FK2/BOVBVR
Sample collection & analysis	The three terms of the freshwater flux are obtained in the following way: Ice discharge: from remotely sensed observations of ice velocity and thickness. The latter is based on a combination of remote sensing and models. Surface melt runoff: from regional climate models. Basal melt: from a combination of remote-sensing data and mathematical models.
Parameters	Ice discharge (icebergs), surface melt and basal melt
Related publications	Mankoff et al. 2019, 2020; Karlsson et al. 2021
Potential application(s) for these data	To quantify the freshwater flux for each glacier; compare different sources of freshwater; resolve the seasonal variability in freshwater flux for different fjords.

Data

The Greenland ice sheet discharges significant volumes of freshwater into the fjords and oceans (Mankoff et al. 2020). This freshwater discharge is known to modify and influence the physical, chemical and biological properties of the fjords and coastal seas (e.g. Hopwood et al. 2020). The combined volume of freshwater that exits from marine-terminating glaciers is currently not readily available on a glacier–basin scale due to disparate data sets. This study presents a data set constructed by combining three publicly available data sets of solid-ice discharge (iceberg), liquid-surface runoff (runoff) and basal melt from the Greenland ice sheet. This new product merges disparate data sets into a product that shares spatial and temporal resolution, enabling easy comparison of mass-loss processes on glacier–basin scales. The following sections give a brief overview of the data sets that form the foundation of the product presented here.

Solid-ice discharge

We use the term ‘solid-ice discharge’ to describe the ice mass that is lost at the marine margin as either icebergs, bergy bits or submarine melt. While this term is traditionally reported as a mass flux in kg or Gt, we convert it to liquid water equivalents to be consistent with the other volume-loss terms.

The solid-ice discharge from more than 200 flux gates situated near the front of marine-terminating glaciers was compiled and presented by Mankoff et al. (2019). Here, we give a brief overview of their methods and results and refer to the original manuscript for details. Mankoff et al. (2019; M2019 for the remainder of this manuscript) calculate ice discharge by considering the mass flow rate through predefined flux gates. The method uses ice thickness and an estimated vertical velocity distribution based on the observed surface velocity, v_s, to calculate the discharge. This may be formulated as:

Where D_g is the ice discharge across a gate, ρ is the average density of ice, V is the depth-averaged horizontal velocity perpendicular to the gate, H is the ice thickness and w is the gate width. In M2019, the velocity v(z) is assumed to be equal at all ice depths, implying that observed surface velocities, v_s, represent depth-averaged velocities (see Enderlin et al. 2014; King et al. 2018), thus assuming V = v_s. In the gate-discharge method, the gate should ideally be at the grounding line of the outlet glacier, where the ice loses contact with its bed and begins to float. In M2019, however, gates are located 5 km from the calving front (which is co-located with the grounding line on most Greenlandic outlet glaciers). The choice of a 5 km distance from the calving front is to keep surface melt between the gate and the front small, while also far enough upstream to minimise errors in bed-location ice thickness that tend to increase towards the calving front (see M2019). For outlet glaciers with ice shelves (as identified in Morlighem et al. 2017), the flux gate is located 5 km from the grounding line. The flux gates are generated by an algorithm ensuring that gate locations can be reproduced or adapted if a glacier outlet changes flow speed or configuration. Ice-flow velocity data are based on data generated from Sentinel 1A and 1B derived by PROMICE (Solgaard et al. 2021), MEaSUREs 0478 and MEaSUREs 0646 (Mouginot et al. 2018a, b; Howat 2017a). The bed topography that provides ice thicknesses at the gates is from BedMachine v3 (Morlighem et al. 2017). The solid-ice discharge data set spans from 1986 to the present day with a temporal resolution ranging from sub-annual to weekly. This data set has a spatial resolution of 200 m at the discharge gates (Mankoff et al. 2019).

Surface-meltwater runoff

The surface-meltwater runoff is the liquid water that drains from the ice sheet as a result of melt and rainfall. The term runoff implies that water retained on the ice sheet is not part of the estimate. The runoff stems from model outputs from regional climate models (RCMs). More information on methods can be found in Mankoff et al. (2020), in the following referred to as M2020. Again, we give a brief overview of the methods and results here and refer to the original Mankoff et al. (2020) manuscript for details.

M2020 estimated Greenland’s liquid-water discharge from surface melt by routing RCM runoff estimates from all points on the ice sheet to the ice margin and coastal outlets. The routing was derived from an ice-sheet surface digital elevation model (DEM), an ice-sheet bed DEM, an ice-sheet mask (Citterio & Ahlstrøm 2013), a land-surface DEM and an ocean mask from the Greenland Ice Mapping Project (GIMP): Land Ice and Ocean Classification Mask, Version 1 (Howat et al. 2014; Howat 2017b). M2020 used ArcticDEM v3 100m (Porter et al. 2018) as the surface DEM while ice thickness from BedMachine v3 (Morlighem et al. 2017) was used to calculate the subglacial routing.

The M2020 data set contains two runoff estimates using two RCM outputs based on the Modèle Atmosphérique Régional (MAR; Fettweis et al. 2017) and the Regional Atmospheric Climate Model (RACMO; Noël et al. 2018), respectively. In both cases, the runoff, R, is defined by:

where ME is melt, RA is rainfall, RT is retention and RF is refreezing. The RCM outputs were re-gridded to the same 1 km grid using offline statistical downscaling (Noël et al. 2016; Fettweis et al. 2020). The model outputs were validated against 10 river-discharge time series with a daily resolution. The final data product from M2020 was daily liquid discharge values from 24 507 ice marginal outlets (that is, ice runoff that discharges at the margin, either on land at the land – water boundary, or subglacially at the ice – ocean boundary) and 29 635 land coast outlets (that is, land-sourced runoff that discharges either at the coast or subglacially). In this work, we only use the ice-sourced runoff that discharges at the ice – ocean boundary.

Basal meltwater

The meltwater specifically caused by subglacial melting, i.e. melt that is separate from surface meltwater, has been quantified by Karlsson et al. (2021), hereafter K2021. Again, we refer the reader to the original manuscript for more details.

In brief, K2021 combined remote-sensing products and modelling to constrain three sources of basal heat in order to obtain local basal-melt rates, b_m:

where E is available energy for the melt, ρ is ice density and L is the latent heat of fusion. The first heat source, the geothermal flux, was constructed as the mean of three different heat-flux models. The second heat source, the frictional heat, was obtained from the full-Stokes ice-flow model Elmer/Ice (Gillet-Chaulet et al. 2012) that emulates present-day ice dynamics by minimising the misfit between modelled and observed surface velocities. The last heat source, viscous-heat dissipation, was estimated by converting the gravitational potential energy of surface meltwater into heat, assuming that all water reaches the bed, essentially providing an upper limit on the available energy. In K2021, surface-meltwater volumes were obtained from the ensemble mean of the Greenland SMB intercomparison project (Fettweis et al. 2020) and routed to the bed using BedMachine v3. The first and second heat sources were masked by an independent estimate of where the ice sheet was likely to be thawed or frozen based on a combination of models and data (MacGregor et al. 2016).

In K2021, the basal-meltwater data set was published as maps specifying basal-melt rates in m yr^–1 for 1 km grid cells and estimates of total basal-meltwater volumes were given mainly as regional totals. In contrast to the two preceding data products, the basal meltwater is only in part temporally changing. The geothermal flux and the friction heat are assumed to be constant while the viscous heat varies with meltwater input.

Changes to the original data set for this study

In M2020, the runoff was routed to the bed of the ice using the topography from BedMachine v3. Here, the topography is updated to BedMachine v4. In this study, we only present runoff derived from MAR and we refer readers to M2020 for a detailed discussion of the similarities between MAR and RACMO.

In K2021, the viscous-heat dissipation was given as the melt resulting from the annual average surface-meltwater volumes for 1995–2010. In this updated data product, the basal melt due to viscous heat has been calculated based on the temporally varying surface-meltwater volumes. Thus, the geothermal and friction terms are constant in time, while the viscous-heat dissipation is resolved monthly using the surface-meltwater volumes from MAR.

Statistical analysis and data processing

We combine the three data sets using the solid-ice discharge gates as our starting point (Fig. 1, yellow lines). The discharge gates are associated with individual glacier outlets or (in some cases) individual tributaries of glaciers. We then tie the surface-meltwater runoff to the discharge gate by identifying individual streamlines that intersect discharge gates (Fig. 1, blue lines). The outlets of these streamlines (Fig. 1, blue dots) are then assigned as belonging to the discharge gate, and the corresponding surface-water basin (Fig. 1, black lines) is associated with the discharge gate. The outline of the surface-water basins was published as part of the M2020 data set. Discharge gates frequently have more than one surface-water basin associated with them; for example, wide glaciers often have several streamlines intersecting their discharge gates. Note that the data presented here only include the surface meltwater that exits via a marine-terminating glacier. Freshwater sources such as land-terminating glaciers, rivers and lakes are not included in our estimate. For these fluxes, we refer to M2020.

Fig. 1 Example from West Greenland showing the three data products. Yellow lines indicate the locations of solid-ice discharge gates from M2020. The surface-meltwater product is shown as blue streamlines with water outlets as purple dots and their associated basins in black. The basal-melt product is shown in red as m/yr. Background image from Satellite background image is from Sentinel-2 (European Space Agency), 20 August 2022.

For the basal-melt component, we calculate the route of each individual grid cell in the basal-melt map to the margin of the ice sheet. When a route intersects a discharge gate, the grid cell and all the grid cells intersected along the route, are assigned as belonging to the discharge gate in question. The subglacial routes are assumed to follow the steepest gradient in the hydropotential (Shreve 1972):

where ρ_w is the density of water, ρ_i is the density of ice, and z_b and z_s are the elevations of bed and surface topography, respectively. This methodology closely resembles the one employed by M2020 when calculating the surface water basins with some exceptions. Here, the surface and bed topographies stem from BedMachine v3 and are smoothed by several ice thicknesses (10 km by 10 km). We perform this smoothing based on several considerations, primarily that the bed topography from BedMachine (regardless of version) is highly uncertain in some areas, which can cause erroneous hydropotential lows leading to the apparent formation of subglacial lakes. This is in contrast with observations showing that there is a limited number of subglacial lakes under the Greenland ice sheet (Livingstone et al. 2022), implying that most subglacial water flows to the margin of the ice sheet in agreement with theoretical considerations of surface and bed slopes (Pattyn 2008). Another consideration is the fact that subglacial water may flow in sediments under the ice; thus, hydropotential lows may be circumvented by water if the bedrock material is porous. We suggest that it is highly likely that water will find a way to travel from areas of high pressure to areas of low pressure (ice-sheet interior to margin). Thus, topographic smoothing is necessary to force water routes to exit at the margin.

In contrast to the basins for the basal melt, the surface-melt basins are not calculated based on a smoothed topography. This difference allows us to explore the impact of topographic smoothing on our results and we discuss this further in the section Uncertainties.

We resample D and R to the same timescale, a monthly volume loss. We chose this timescale as a pragmatic common time. R is model-derived and available daily. The temporal resolution of D varies from seasonal to sub-monthly depending on satellite acquisition timing. Where necessary, D is linearly interpolated in time if the data are not available monthly.

Data description and main features

Our data set represents 267 individual discharge gates. The freshwater flux from each discharge gate is accessible as a csv file with the naming convention GLACIERNAME_REGION_GATE.csv, where the glacier name is the official Greenlandic name (following Bjørk et al. 2015 and the Oqaasileriffik placename database maintained by Asiaq), the region follows the naming convention from Mouginot et al. (2019c; see Fig. 3) and ‘gate’ is the gate id from M2019. The data set is accompanied by a metadata text file and a file containing geographical information and naming convention for each gate.

Here, we present the contents of the data set using the three glaciers shown in Fig. 1 as an example. Figure 2a, b, c show the monthly surface runoff, solid-ice discharge, and basal melt for the glaciers Salliarutsip Sermia, Umiammakku Sermiat and Kangilliup Sermia (Rink Isbræ) for 2010–2020. All three glaciers experienced large surface melt in 2012 and again in 2019. In comparison, the solid-ice discharge has lower variability – although Kangilliup Sermia has distinct variations in solid-ice discharge during the year, often with a winter minimum. Note that the y-axis is different by an order of magnitude for Kangilliup Sermia. This is clearly seen in Fig. 2d. The temporal resolution of our data makes it possible to consider the seasonality of the volume loss. Figure 2e shows the summer and winter volume loss, where summer is defined as the months April through September while winter is defined as October through March. Most volume loss happens during the summer months for all three glaciers, but Kangilliup Sermia has a larger proportion of winter volume loss, including liquid volume loss, compared to its neighbours.

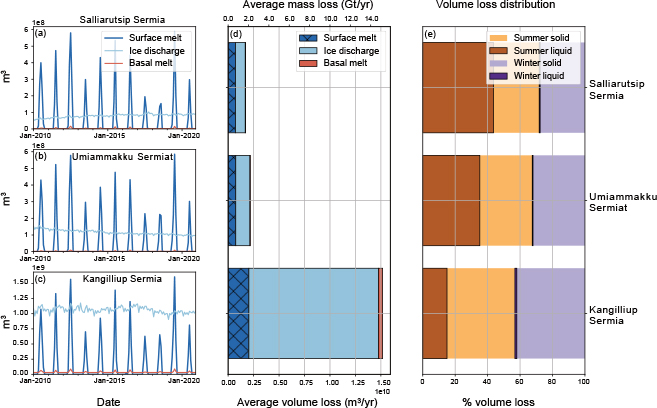
Fig. 2 Monthly volume loss terms as attributed to different processes for glaciers. (a) Salliarutsip Sermia. (b) Umiammakku Sermiat. (c) Kangilliup Sermia (locations in Fig. 1). We partition the volume loss into surface melt (dark blue), iceberg calving (light blue) and basal melt (magenta). For comparison are (d) average annual volume loss for 2010–2020 and (e) relative seasonal distribution of volume loss for the same period. Official Greenlandic names from Bjørk et al. (2015).

According to our full data set, all marine-terminating glaciers in Greenland lose more volume during the summer than the winter. However, the distribution of the volume loss varies. For example, 32 glaciers have a winter volume loss that is close to summer volume loss, including glaciers Arfalluarfiup Sermia (Diebitsch, NW region; regions indicated in Fig. 3), Apuseeq Qinnilik (CE region) and Nunatakassaap Sermia (Alison Gletscher, NW region). At the other end of the scale, 16 glaciers experience 95% of their volume loss during the summer. This includes glaciers Apuseeq (Køge Bugt, regions N and SE), Waltershausen Gletscher (NE region) and Kangiata Nunaata Sermia (SW region).

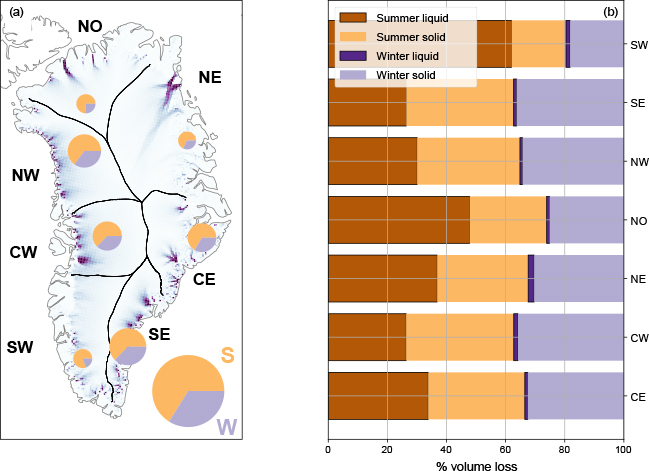
Fig. 3 Seasonality of all regions in Greenland. (a) Summer (brown) and winter (purple) volume loss for each region where the size of the circles indicates the total volume loss. The background image shows ice-flow velocities from MEaSURES (Joughin 2020). (b) Same as (a) but as bars. The proportion of the volume loss that is liquid is shown with darker colours and a black outline. The seven regions are defined by Mouginot et al. 2019c as follows: south-west (SW), central west (CW), north-west (NW), north (NO), north-east (NE), central east (CE), and south-east (SE).

We can expand on this analysis and consider regional differences. Figure 3 shows the seasonal distribution of volume loss from all discharge gates reported from the seven regions of Greenland. All regions experience more volume loss during the summer than during the winter but with some regional differences. The regions SE and CW experience 38% of their volume loss during the winter months while in comparison winter volume loss from SW and NO regions accounts for 20% and 26% of annual volume loss, respectively. The regions NE and SW have the largest proportion of winter volume loss as liquid, 6% and 7%, respectively. Table 1 details the average monthly volume loss from each region during the winter and summer months. Table 2 shows regional annual averages of solid- and liquid-volume loss.

Table 1 Volume loss in solid and liquid form

Region	Average monthly solid flux (October–March), 107 m3	Average monthly liquid flux (October–March), 107 m3	Average monthly solid flux (April–September), 107 m3	Average monthly liquid flux (April–September), 107 m3
CE	12 ± 3	0.4 ± 0.1	12 ± 3	13 ± 4
CW	45 ± 12	1.8 ± 0.5	46 ± 13	33 ± 9
NE	29 ± 8	1.9 ± 0.5	29 ± 8	33 ± 9
NO	11 ± 3	0.4 ± 0.1	12 ± 3	22 ± 6
NW	13 ± 4	0.3 ± 0.1	13 ± 4	11 ± 3
SE	13 ± 4	0.4 ± 0.1	13 ± 4	10 ± 3
SW	12 ± 3	0.9 ± 0.3	12 ± 3	37 ± 10
Total	136 ± 38	6.1 ± 1.7	138 ± 38	159 ± 45
The table shows the average flux during 2010–2020 for the winter months (October through March) and summer months (April through September) in units of 107 m3. The seven regions are defined in Fig. 3: south-west (SW), central west (CW), north-west (NW), north (NO), north-east (NE), central east (CE), and south-east (SE).

 

Table 2 Annually averaged volume loss in solid and liquid form (2010–2020)

Region	Annual average solid flux, 109 m3	Annual average liquid flux, 109 m3	Total flux, 109 m3
CE	76.7 ± 21.5	41.0 ± 11.5	117.7 ± 33.0
CW	87.7 ± 24.5	33.8 ± 9.5	121.4 ± 34.0
NE	27.8 ± 7.8	17.7 ± 5.0	45.5 ± 12.7
NO	26.7 ± 7.5	25.4 ± 7.1	52.1 ± 14.6
NW	109.1 ± 30.6	49.0 ± 13.7	158.2 ± 44.3
SE	140.9 ± 39.5	53.4 ± 14.9	194.3 ± 54.4
SW	18.8 ± 5.3	32.5 ± 9.1	51.3 ± 14.4
The seven regions are defined in Fig. 3: south-west (SW), central west (CW), north-west (NW), north (NO), north-east (NE), central east (CE), and south-east (SE).

Uncertainties

The uncertainties associated with our data set fall into two categories: (1) those inherited from the data sets upon which we have constructed ours and (2) those associated with constructing the drainage basins.

For the former, we adopt the uncertainties as stated in the M2019, M2020 and K2021 data sets. Following M2019, the ice-discharge uncertainties are within 10%. Uncertainties primarily stem from unknown or poorly sampled ice thicknesses and uncertainties in the surface-velocity data. We refer the reader to M2019, Appendix A for a thorough discussion of their treatment of uncertainties.

The runoff is influenced by several different kinds of uncertainties, including uncertainty in the delay between melt (at a location on the ice sheet) and discharge of the water at the margin, uncertainties associated with the RCMs that generate the meltwater volume, and the uncertainty in the basin delineation. M2020 discusses these uncertainties in detail but refrains from stating a global uncertainty, noting that depending on local glacier settings, the uncertainties likely vary substantially between sites. Particularly small basins are likely to be subject to substantial errors due to basin delineation. The stated uncertainty for the RCMs is 15%. We advise users of our data set to consider this as a lower boundary.

The uncertainty associated with the basal-melt data set is also spatially variable and stems from the fact that basal conditions of the Greenland ice sheet are widely unknown, including the poorly constrained geothermal flux. K2021 uses an asymmetrical uncertainty range to capture the full possibility of basal conditions. Here, for simplicity and to be consistent with M2019 and M2020, we use the largest uncertainty as a conservative estimate at 21%. Again, we refer readers to K2021 for a more detailed discussion of the different uncertainties.

Combining the uncertainty ranges listed above using root-sum square, we estimate the overall uncertainty to be 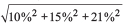= 28% as a lower boundary, although we note that uncertainties are not independent, even though we treat them as such.

The uncertainty associated with constructing the drainage basins is also thoroughly discussed in M2020 in connection with the surface-meltwater product. To further investigate the uncertainty, we compare the basins constructed in this work based on smoothed surface and bed topography to the basins from M2020. By far the biggest difference between drainage basins is found in North-East Greenland. In M2020, the outlet named Zachariae Isstrøm drains a large part of the region, while in this study the main outlet is Spaltegletsjer (Nioghalvfjerdsfjorden). The change is so large that the basin size changes by 98% for Zachariæ. The second largest difference in basin size occurs for Kjer Gletsjer in North-West Greenland, which shrinks in size by 6.7e¹⁰ m² or several multitudes of its original size. Supplementary Table 1 summarises the 10 largest differences in basins between M2020 and this study. Although the values look prohibitively large, we note that 28% of basins change in size by less than 20%. Due to the large variability in the basins discussed here, we do not quantify the uncertainty related to the basins, noting that small basins are likely to be particularly uncertain.

Acknowledgments

NBK thanks N. Damgaard for helpful insights and advice on figure designs. The authors thank T. Black for a very thorough and constructive review that greatly improved this manuscript. We also thank two anonymous reviewers for valuable comments and suggestions, and handling editor M-S Seidenkrantz.

Funding statement

This work was supported by the Polar+ 4D Greenland project (2020–2022), which was funded by the European Space Agency (ESA) via ESA Contract No. 4000132139\I-EF and by PROMICE, which is funded by the Geological Survey of Denmark and Greenland (GEUS) and the Danish Ministry of Climate, Energy and Utilities under the Danish Cooperation for Environment in the Arctic (DANCEA), and is conducted in collaboration with DTU Space (Technical University of Denmark) and Asiaq, Greenland.

Author contributions

NBK: Conceptualisation, Data curation, Formal Analysis, Funding acquisition, Methodology, Visualisation, Writing.

KDM: Data curation, Methodology, Validation, Writing.

AMS: Data curation, Methodology, Funding acquisition, Methodology, Writing.

SHL: Methodology, Validation, Writing.

PRH: Resources, Software, Writing.

RSF: Funding acquisition, Project administration, Writing.

LSS: Funding acquisition, Project administration, Writing.

Additional files

Supplementary Table 1 along with modelled and reformatted data are available at https://doi.org/10.22008/FK2/BOVBVR

References

Bjørk, A.A., Kruse, L.M. & Michaelsen, P.B. 2015: Brief communication: getting Greenland’s glaciers right – a new data set of all official Greenlandic glacier names. The Cryosphere 9(6), 2215–2218. https://doi.org/10.5194/tc-9-2215-2015

Citterio, M. & Ahlstrøm, A.P. 2013: Brief communication ‘the aerophotogrammetric map of Greenland ice masses’. The Cryosphere 7(2), 445–449. https://doi.org/10.5194/tc-7-445-2013

Enderlin, E.M., Howat, I.M., Jeong, S., Noh, M.-J., van Hangelen, J.H. & van den Broeke, M.R. 2014: An improved mass budget for the Greenland ice sheet. Geophysical Research Letters 41, 866–872. https://doi.org/10.1002/2013gl059010

Fettweis, X., Box, J.E., Agosta, C., Amory, C., Kittel, C., Lang, C., van As, D., Machguth, H. & Gallée, H. 2017: Reconstructions of the 1900–2015 Greenland ice sheet surface mass balance using the regional climate MAR model. The Cryosphere 11(2), 1015–1033. https://doi.org/10.5194/tc-11-1015-2017

Fettweis, X. et al. 2020: GrSMBMIP: intercomparison of the modelled 1980–2012 surface mass balance over the Greenland ice sheet. The Cryosphere 14(11), 3935–3958. https://doi.org/10.5194/tc-14-3935-2020

Gillet-Chaulet, F., Gagliardini, O., Seddik, H., Nodet, M., Durand, G., Ritz, C., Zwinger, T., Greve, R. & Vaughan, D.G. 2012: Greenland ice sheet contribution to sea-level rise from a new-generation ice-sheet model. The Cryosphere 6(6), 1561–1576. https://doi.org/10.5194/tc-6-1561-2012

Hopwood, M.J. et al. 2020: Review article: how does glacier discharge affect marine biogeochemistry and primary production in the Arctic? The Cryosphere 14, 1347–1383. https://doi.org/10.5194/tc-14-1347-2020

Howat, I. 2017a: MEaSUREs Greenland ice velocity: selected glacier site velocity maps from optical images. Version 2. NASA National Snow and Ice Data Center Distributed Active Archive Center. https://doi.org/10.5067/VM5DZ20MYF5C

Howat, I. 2017b: MEaSUREs Greenland ice mapping project (GIMP) land ice and ocean classification mask. Version 1. NASA National Snow and Ice Data Center Distributed Active Archive Center. https://doi.org/10.5067/B8X58MQBFUPA

Howat, I.M., Negrete, A. & Smith, B.E. 2014: The Greenland ice mapping project (GIMP) land classification and surface elevation data sets. The Cryosphere 8(4), 1509–1518. https://doi.org/10.5194/tc-8-1509-2014

Joughin, I. 2020: MEaSUREs Greenland annual ice sheet velocity mosaics from SAR and Landsat. Version 2. NASA National Snow and Ice Data Center Distributed Active Archive Center. https://doi.org/10.5067/TZZDYD94IMJB

Karlsson, N.B. et al. 2021: A first constraint on basal melt-water production of the Greenland ice sheet. Nature Communications 12, 3461. https://doi.org/10.1038/s41467-021-23739-z

King, M.D., Howat, I.M., Jeong, S., Noh, M.J., Wouters, B., Noël, B. & van den Broeke, M.R. 2018: Seasonal to decadal variability in ice discharge from the Greenland ice sheet. The Cryosphere 12(12), 3813–3825. https://doi.org/10.5194/tc-12-3813-2018

Livingstone, S.J. et al. 2022: Subglacial lakes and their changing role in a warming climate. Nature Reviews Earth & Environment 3, 106–124. https://doi.org/10.1038/s43017-021-00246-9

MacGregor, J.A. et al. 2016: A synthesis of the basal thermal state of the Greenland ice sheet. Journal of Geophysical Research: Earth Surface 121(7), 1328–1350. https://doi.org/10.1002/2015jf003803

Mankoff, K.D. et al. 2019: Greenland ice sheet solid ice discharge from 1986 through 2017, Earth System Science Data 11, 769–786. https://doi.org/10.5194/essd-11-769-2019

Mankoff, K.D., Noël, B., Fettweis, X., Ahlstrøm, A.P., Colgan, W., Kondo, K., Langley, K., Sugiyama, S., van As, D. & Fausto, R.S. 2020: Greenland liquid water discharge from 1958 through 2019. Earth System Science Data 12(4), 2811–2841. https://doi.org/10.5194/essd-12-2811-2020

Morlighem, M. et al. 2017: BedMachine v3: complete bed topography and ocean bathymetry mapping of Greenland from multibeam echo sounding combined with mass conservation. Geophysical Research Letters 44(21), 11051–11061 https://doi.org/10.1002/2017gl074954

Mouginot, J., Rignot, E., Millan, R., Wood, M. & Scheuchl, B. 2019a: Annual ice velocity of the Greenland ice sheet (1972–1990). Dryad, dataset. https://doi.org/10.7280/D1MM37

Mouginot, J., Rignot, E., Scheuchl, B., Millan, R. & Wood, M. 2019b: Annual ice velocity of the Greenland ice sheet (1991–2000). Dryad, dataset. https://doi.org/10.7280/D1GW91

Mouginot, J., Rignot, E., Bjørk, A.A., van den Broeke, M., Millan, R., Morlighem, M., Noël, B., Scheuchl, B. & Wood, M. 2019c: Forty-six years of Greenland ice sheet mass balance from 1972 to 2018. Proceedings of the National Academy of Sciences 116, 9239–9244. https://doi.org/10.1073/pnas.1904242116

Noël, B., van de Berg, W.J., Machguth, H., Lhermitte, S., Howat, I., Fettweis, X. & van den Broeke, M.R. 2016: A daily, 1 km resolution data set of downscaled Greenland ice sheet surface mass balance (1958–2015). The Cryosphere 10(5), 2361–2377. https://doi.org/10.5194/tc-10-2361-2016

Noël, B. et al. 2018: Modelling the climate and surface mass balance of polar ice sheets using RACMO2 – Part 1: Greenland (1958–2016). The Cryosphere 12, 811–831. https://doi.org/10.5194/tc-12-811-2018

Pattyn, F. 2008: Investigating the stability of subglacial lakes with a full stokes ice-sheet model. Journal of Glaciology 54(185), 353–361. https://doi.org/10.3189/002214308784886171

Porter, C. et al. 2018: ArcticDEM V3. Havard Dataverse. https://doi.org/10.7910/DVN/OHHUKH

Shreve, R.L. 1972: Movement of water in glaciers. Journal of Glaciology 11(62), 205–214. https://doi.org/10.3189/s002214300002219x

Solgaard, A. et al. 2021: Greenland ice velocity maps from the PROMICE project. Earth System Science Data 13(7), 3491–3512. https://doi.org/10.5194/essd-13-3491-2021