MONOGRAPH

Petrology of the Skaergaard Layered Series

Peter Thy,^1* Christian Tegner² and Charles E. Lesher^1,2

¹Department of Earth and Planetary Sciences, University of California, Davis, USA; ²Department of Geoscience, Aarhus University, Aarhus, Denmark

Abstract

The Skaergaard intrusion is a layered, ferrobasaltic intrusion emplaced during the Early Eocene into the rifting volcanic margin of East Greenland. The magma chamber crystallised in response to cooling from the roof and margins upwards and inward, forming upper, marginal and bottom series, the latter referred to as the Layered Series. The phase layering in the bottom series suggests an evolved, olivine-normative tholeiitic melt saturated in plagioclase and olivine, followed by augite, and then simultaneously by ilmenite and magnetite forming primocrysts. Pigeonite appears in the lower parts and continues until the centre of the series. Apatite appears in the upper part concurrently with liquid immiscibility. Cryptic variations of the individual primocrysts record a systematic upward increase in iron and decrease in magnesium for the mafic minerals and a systematic increase in sodium and decrease in calcium for plagioclase. The appearance of pigeonite is caused by reactions and crystallisation in the trapped melt and by subsolidus adjustments without this phase reaching liquidus saturation. The high mode of olivine at the base of the upper part with the appearance of apatite is interpreted to mark the onset of liquid immiscibility. This may have led to the separation of conjugate melts with granophyre migrating upward and the basic component largely staying stationary or sinking. Petrologic and geochemical observations indicate differentiation in the lower part of the intrusion, principally controlled by crystal fractionation with the efficiency of fractionation controlled by the evolution and escape of liquid from the solidifying mush. During the final stages of solidification, the onset of liquid immiscibility and termination of melt convection impeded differentiation. Modelling by perfect Rayleigh fractionation shows that major and included trace elements conform reasonably to observations, while excluded elements deviate from model predictions. This decoupling is caused by the mobility of a granophyre component formed in the trapped melt and in the main residual magma chamber. Consequently, the sampled gabbros may not be representative of the final solid-melt mush. By restoring the gabbros to their original mush compositions, it is possible to constrain granophyre migration pathways. We suggest that the granophyre formed in the trapped melt in the lower part of the intrusion mostly migrated laterally through pressure release pathways to form lenses and pockets with only limited upward migration into the main magma reservoir. Near the end stage of differentiation, the residual magma exsolved and formed complex mixtures of ferrobasaltic and granophyric melts. Estimates predict that a substantial amount of the granophyric melt penetrated as sills into the downward crystallising, upper part of the body as well as into the host rocks. The redistribution of granophyric melts within the solidifying crystal mush complicates predictions of trapped-melt content and mass-balance calculations but helps to explain apparent decoupling of included and excluded trace elements, especially towards the end stages of evolution. Final crystallisation was controlled mostly by in situ crystallisation leaving complex mixtures of ferrodiorite and granophyre components.

1 Introduction

Basaltic lavas extruded and quenched on the surface of the Earth, such as on the sea floor and continental margins and crust, record a complex history of deep-seated melting and crystallisation. These lavas also record the reactive interactions with the host rocks during their upward migration and transient storage in reservoirs, as well as low-temperature water-rock interaction and hydrothermal alteration. Because we can sample and analyse extruded lavas, we may be able to deduce their formation and history using various observational, experimental and theory-based modelling approaches (e.g. Langmuir et al. 1992; O’Hara & Herzberg 2002; Brown & Lesher 2014).

Despite not being directly observed, temporary storage in crustal chambers has proven necessary for explaining the observed differentiation pattern in many extruded magmas. An important source for our understanding of the role of such magma chambers and related chamber processes has come from studies of tectonically uplifted sea-floor fragments (or ophiolites; e.g. Coleman 1977; Pallister & Hopson 1981; Thy et al. 1989; Thy & Dilek 2000, 2003; Bédard 2015). Additional information has come from seismic studies of active centres of sea-floor spreading (Sinton & Detrick 1992; Morgan et al. 1994) and from direct drilling into ocean crust near spreading centres (Natland et al. 1991; Dick et al. 2000; Thy 2003).

The chamber view that has emerged for steady-state settings of sea-floor spreading is one in which the chamber extends downwards as a zone filled with crystal mush, centred under the spreading ridge and capped by a smaller magma lens maintained by upward migrating fresh melt and interstitial melt migration aided by compaction of the crystal mush (Nisbet & Fowler 1978; Sinton & Detrick 1992; Kelemen et al. 1997). Flux of fresh, mantle-derived magma upwards in the mush may stabilise as sill-like bodies forming sill complexes (Kelemen et al. 1997). The notion of such transitional crystal-mush zones beneath volcanic systems have been heralded as a unifying conceptual model that can explain features of both axial and off-axial volcanic systems (Cashman et al. 2017; Sparks et al. 2019). It is thought to explain, on the one hand, a slow, steady incremental influx of melt, originating deeper in the crust or mantle and building up large mush reservoirs, and on the other hand, episodic large-volume eruptions in the form of plateau lavas. The observation that large-volume magma chambers are often not detected in the crust leads to the suggestion that magmatic melt is, instead, stored in mush reservoirs, only to be activated just prior to eruption on the surface or accumulated in shallower chambers if direct gateways to the surface are not easily available (Edmonds et al. 2019; Holness et al. 2019; Sparks et al. 2019). Shallow melt emplacement and trapping in melt-dominated chambers are important building blocks for crustal accretion (Bachmann et al. 2007; Edmonds et al. 2019).

Although systematic studies of ophiolitic ultramafic and gabbro complexes are relatively few (Thy & Dilek 2000, 2003), those which do exist reveal a range of magma chambers. These include a steady-state, sea-floor spreading-related chamber that may represent a crustal-mush zone (Pallister & Hopson 1981; Kelemen et al. 1997), backarc-related chambers (Thy et al. 1989) and continental rift chambers (Church & Riccio 1977; Bédard 2015) that record infrequently replenished, melt-dominated chambers and thus magmatic settings controlled by restricted upward flux of melt.

An equally important source for understanding basaltic magma chambers has been melt-dominated plutons intruded into continental settings. Most prominent of these, among many, have been the Stillwater Complex of Montana (Hess 1960; Jackson 1961; Page 1979; McCallum 1996), the Kiglapait intrusion of the anorthositic Nain Complex in Labrador (Morse 1969, 2015), the Rhum (or Rum) complex of the Inner Hebrides, Scotland (Brown 1956; Tait 1985), the ultramafic Jurassic-Cretaceous Duke Island complex of south-eastern Alaska (Irvine 1974), the Precambrian Muskox intrusion of the Canadian Northwest Territories (Irvine 1980), the synorogenetic Fongen-Hyllingen intrusion of the central Norwegian Caledonides (Wilson et al. 1981; Wilson & Larsen 1985; Wilson & Sørensen 1996), the Precambrian Bushveld Complex in the Transvaal of South Africa (Daly 1928; Eales & Cawthorn 1996; Cawthorn 2015) and finally the Tertiary Skaergaard intrusion of East Greenland (Wager & Deer 1939; Wager & Brown 1967; McBirney 1995, 1996; Brooks 2011; Holness et al. 2017a). This latter intrusion was emplaced into continental crust during the rift-to-drift transition leading to formation of the North Atlantic Ocean basin and is the focus of the present study (Fig. 1).

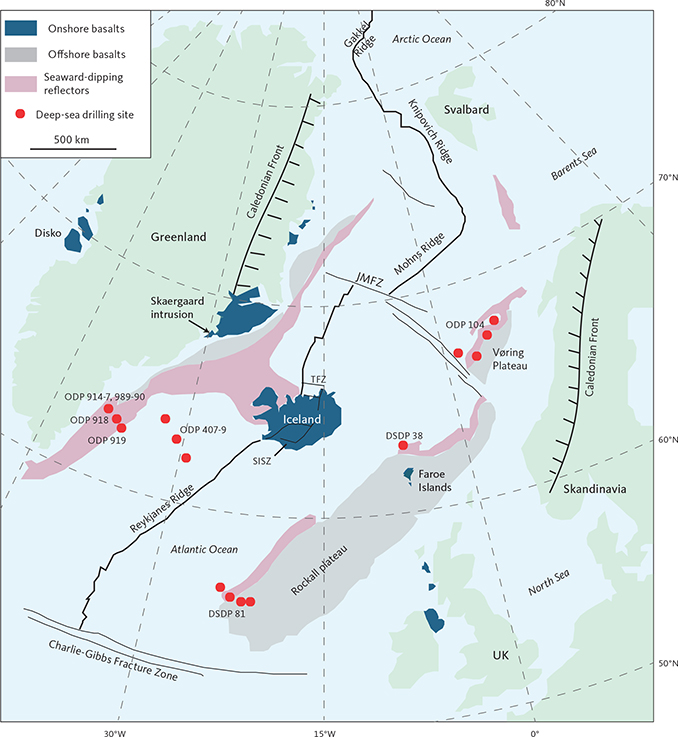
Fig. 1 North Atlantic Igneous Province as outlined by sea-floor spreading ridges, major fracture zones and continental-bordering areas. Shown are onshore and offshore basalts, seismic dipping reflector sequences, the Caledonian fronts and deep-sea drilling sites, prefixed ODP (ocean drilling programme) or DSDP (deep-sea drilling programme). TFZ: Tjörnes Fracture Zone; JMFZ: Jan Mayen Fracture Zone; SISZ: South Iceland Seismic Zone. Location of the Skaergaard intrusion is marked at 68°10´ N, 31°40´ W. Map is modified from Brooks (2011).

These ultramafic to gabbroic plutons represent wide ranges in terms of initial melt composition, volume, depth of intrusion and structural and tectonic history of emplacement. There are, however, some commonalities that often characterise their solidification and cooling histories. Typically, the plutons reveal overall internal systematic differentiation patterns that correlate with the inferred decreasing magma temperature (T), often from the base to the top of a melt-dominated stratigraphy. In many cases, the overall differentiation trend is interrupted and reversed for shorter periods due to magma recharge. Additionally, they display complex layering defined by modal and size variations of the constituent minerals. Such plutons are typically melt-dominated and are referred to as layered intrusions.

Differentiation is recorded in the mineral assemblages (phase layering) with the minerals and modal proportions constrained by known basaltic phase equilibria. Additionally, differentiation is recorded in mineral compositions (cryptic layering) and shows systematic changes in sodium (plagioclase) or iron (olivine and pyroxenes) contents increasing with decreasing temperature and fraction of melt remaining (F) upward or inward in the plutons. The observed differentiation is mainly attributed to fractional crystallisation due to cooling, but may also be related to magma mixing, assimilation of country rocks, liquid immiscibility and fluid exsolution. The separation of crystals from the bulk melt is widely believed to either be due to (1) gravitational accumulation and compaction, (2) crystallisation on a melt-solid interface (hard ground), (3) crystallisation in a bottom-mush zone (soft ground) or some combination of these processes. Regardless, the result is the formation of melt-solid interface mushes made of liquidus primocrysts (often referred to as cumulus phases) and variable proportions of interstitial crystals and crystal rims that grew from interstitial melts. The latter two options are referred to as in situ crystallisation processes, where a solidification boundary melt is completely or partially recycled back into the main magma chamber where differentiation is driven by convection and homogenisation.

In contrast to extruded lavas, the rocks of slowly cooled intrusions do not preserve the melt from which they crystallised. Moreover, melts in the mush can crystallise, migrate or react with host minerals during growth and cooling. Thus, in situ crystallisation, compaction and melt convection or migration and reactions all contribute to the demise of interstitial melt. However, their various contributions are challenging to detect and even more difficult to quantify.

It is the purpose of this study to review much of what is understood about such differentiation processes as exemplified by the Skaergaard intrusion (Fig. 1). We present petrographic, mineralogical and major and trace element data of the main Layered Series (LS) collected during ground traverses and from a drill core. This suite of samples constitutes a composite profile through the LS (Tegner et al. 2009) that closely follows the previously constructed profiles through the central portion of the LS by Wager & Deer (1939), Wager & Brown (1967) and McBirney (1989a).

We begin with a brief overview of the Skaergaard intrusion, followed by a summary of methods and then a description of the petrography upon which the internal structure or zonal divisions are based. From there we examine mineral and bulk-rock variations that form the observational basis for petrologic modelling. In the following sections, we synthesise the great volume of previous work and use our new data to constrain the liquid line of descent and to evaluate proposed and potentially competing models of differentiation for the Skaergaard intrusion.

A set of appendices are provided at the end of this manuscript that includes additional historical background (Appendix 1), information on sampling and construction of the composite profile (Appendix 2) and analytical methods and mode determinations (Appendix 3). Included as online supplementary files is a collection of data tables, photomicrographs and summaries of modelling results. It is our hope that future researchers working on the Skaergaard intrusion and similar plutons will find these compilations useful in their own research and that the archive will be a valuable resource for courses in petrology and geochemistry. To better facilitate the latter, we also include the original sample location maps by L.R. Wager and A.R. McBirney, geological and topographical maps, together with a set of stereoscopic aerial colour photos of the Skaergaard intrusion and surroundings as online supplementary files.

2 The Skaergaard intrusion

The Skaergaard intrusion is a relatively small (c. 300 km³) melt-dominated pluton that has been repeatedly and extensively studied because of the field exposure, due to glacial erosion, of a near complete and uninterrupted sequence of fractionated basaltic gabbros. The common explanation is that the Skaergaard magma chamber was emplaced as one pulse or a series of rapid pulses at a high level in the East Greenland crust and cooled relatively quickly with little interaction with its host rocks (approximating a closed system).

The intrusion was discovered in 1930 in the Kangerlussuaq Fjord of East Greenland by L.R. Wager and described in detail by Wager & Deer (1939). Since then, the intrusion has provided exceptional insights into the crystallisation and solidification of basaltic magma chambers (e.g. Wager & Brown 1967; McBirney 1995; Irvine et al. 1998; Holness et al. 2017a). A summary of the history of the exploration of the intrusion can be found in Appendix 1; for more details the reader is referred to Brooks (2018).

The Skaergaard intrusion intruded at 68°10’N and 31°40’W during continental rifting of the East Greenland continental margin (Fig. 1; Brooks 2011) at a high crustal level at the contact between Precambrian gneisses and overlying Eocene plateau basalts, which preserve a well-defined metamorphic contact aureole and a chilled margin (Wager & Deer 1939; Hoover 1989a; Kays et al. 1989; Bufe et al. 2014). The chamber was initiated by small pulses of magma, followed by a large influx that inflated the chamber to its maximum (Holness et al. 2015), and this resulted in the present box-shaped intrusion controlled largely by normal faulting (Irvine 1991; Nielsen 2004). The intrusion was emplaced around 55.4–56.6 Ma (Hirschman et al. 1997; Tegner et al. 2008; Brooks 2011; Wotzlaw et al. 2012), coinciding with the formation of the main plateau lavas (Larsen et al. 1989; Tegner et al. 1998; Larsen & Tegner 2006) and the transition from rift to drift tectonics of the North Atlantic (Storey et al. 2007; Tegner et al. 2008; Brooks 2011).

As a result of initial cooling, a marginal gabbro (including a chilled margin) formed against the country rocks. The subsequent crystallisation proceeded upward and inwards from the margins of the chamber (Fig. 2A). The Marginal Border Series and Upper Border Series (MBS and UBS, respectively) formed by crystallisation from the walls and roof of the chamber (Naslund 1984; Hoover 1989a, b; Salmonsen & Tegner 2013), respectively, and the Layered Series (LS) formed concurrently upward from the floor of the chamber (McBirney 1989a). The crystallisation fronts eventually converged at the position of the Sandwich Horizon (SH). As a result, three differentiated stratigraphic sections formed in different positions relative to gravity (Figs 2A, B) that allow detailed assessments of the solidification processes (Wager & Deer 1939; Wager & Brown 1967; McBirney 1995). It has been proposed that candidate liquids for the initial Skaergaard magma occur as coeval dykes intruding basement gneiss in the vicinity of the intrusion (Nielsen 1978) and are found among the plateau lavas of East Greenland (Larsen et al. 1989; Tegner et al. 1998; Andreasen et al. 2004; Larsen & Tegner 2006; Jakobsen et al. 2010: Nielsen et al. 2019a; Cho et al. 2022).

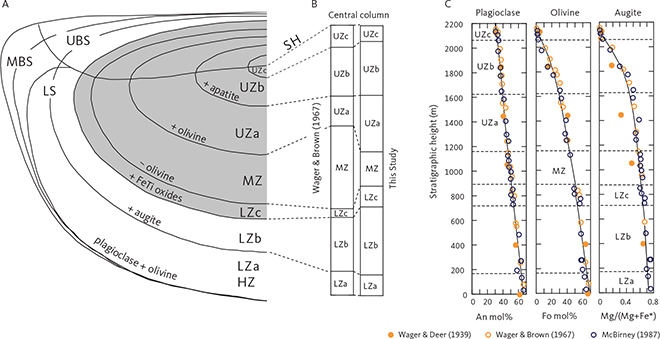
Fig. 2 Summary of the Skaergaard intrusion and its Layered Series (LS). A: Schematic representation of the Skaergaard intrusion showing the main divisions of the LS after McBirney (1995) and Nielsen (2004). MBS: Marginal Border Series. UBS: Upper Border Series. HZ: Hidden Zone. LZ: Lower Zone (with subdivisions a to c). MZ: Middle Zone. UZ: Upper Zone (with subdivisions a to c). SH: Sandwich Horizon. The HZ and LZa have been grouped together. The presence (+) and absence (–) of the main minerals used to define the zone divisions are indicated following Wager & Brown (1967). B: Comparison of the central profile as measured by Wager & Brown (1967) and as used in this study. C: The cryptic variation in the central profile of the LS as seen for plagioclase (An mol%), olivine (Fo mol%) and augite (Mg/(Mg + Fe^*) ratio) on an atomic basis with all iron calculated as total ferrous iron. Data from Wager & Deer (1939), Wager & Brown (1967) and McBirney (1989a). All data have been projected onto the stratigraphic column of this study. The solid curves are the best visual fit to the data of Wager & Brown (1967), extended to the full stratigraphic occurrences irrespective of primocryst status.

The principal manifestation of the evolution of the parental magma is a systematic mineralogical enrichment in low-temperature components or end members, like albite and fayalite, of the constituent minerals upward and towards the centre of the intrusion (Fig. 2C). An equally important manifestation is the systematic appearance and disappearance of minerals (phase layering) with falling temperature, which can be related to crystallisation behaviour in simple basaltic systems (Osborn 1959; Presnall 1966; Irvine 1970a, 1979; Ford 1981). This allows the layered and border series to be divided into primocryst zones and subzones, defined by the presence or absence of minerals (Figs 2A, B). These zonal divisions provide convenient reference horizons for tracking magmatic evolution within the chamber (Wager & Brown 1967).

The prominent role of the intrusion in shaping modern petrologic theories is not only due to the intrusion’s unique coastal glacial-shaped exposure, but perhaps more importantly due to the fundamental compositional and petrographic information that L.R. Wager and his co-workers painstakingly collected through the central parts of the intrusion over nearly half a century of work (Fig. 2C). Wager & Deer (1939) constructed their original stratigraphic profile through the LS of the intrusion using approximately only eight samples to define the cryptic mineral compositional variation (Fig. 3B). Wager & Brown (1967) later produced a more detailed record (Fig. 3B). A drill core obtained in 1966 penetrated about 150 m into the Hidden Zone (HZ) and extended the central profile to slightly deeper levels (Fig. 3A; Maaløe 1976a; Nwe 1976; Holness et al. 2015; Brooks 2018). McBirney (1989a) defined three laterally positioned parallel profiles (west, central and east) of which the central profile was located close to the original profile constructed by Wager & Deer (1939). A summary of the cryptic mineral variation defined by these early studies in the central column of the intrusion and re-scaled to the stratigraphic column of this study is illustrated in Fig. 1C (Wager & Deer 1939; Wager & Brown 1967; McBirney 1989a).

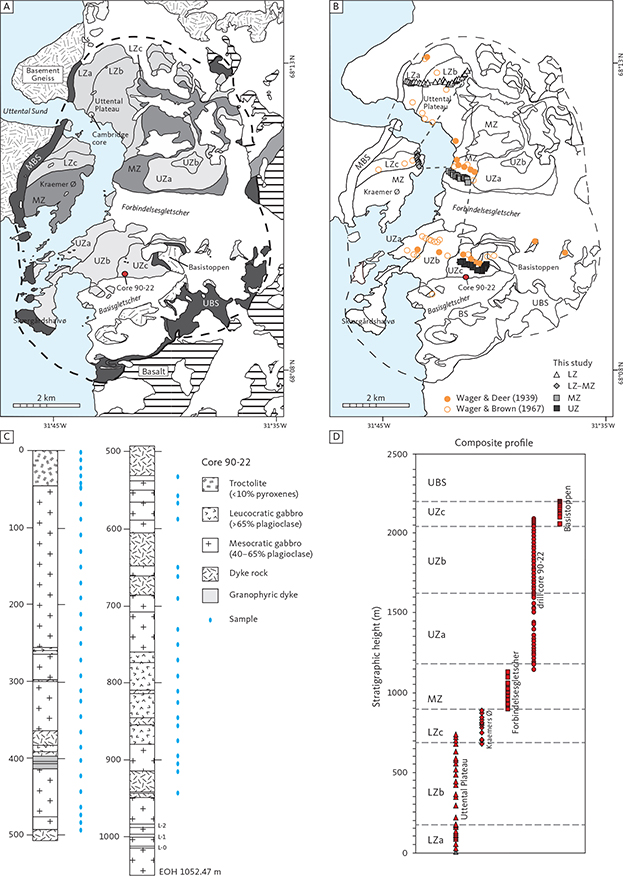
Fig. 3 Location of samples and the drill core used in the present study. A: Geological map after McBirney (1989b). B: Locality map for the present study as well as the approximate localities used for the profiles constructed by Wager & Deer (1939) and Wager & Brown (1967). The grey dashed line marks the profile of this study. The central profile constructed by McBirney (1989a; not shown) largely follows the general trend of Wager & Deer (1939). C: Drill core 90-22 with dominating petrography and sample positions shown (Watts, Griffis & McOuat Ltd. 1991). L-0, L-1 and L-2 refer to the Triple Group of prominent felsic layers and the host of the Skaergaard PGE-Au Mineralisation. D: Construction of the composite profile after Tegner et al. (2009). EOH: end of hole. Other abbreviations in Fig. 2.

The opportunity to re-sample the central profile of the Skaergaard intrusion was offered following the decision by the Geological Survey of Denmark and Greenland (GEUS) to salvage and transport to Copenhagen some of the most important exploratory drill cores made in 1993 by Platinova in the upper part of the intrusion. In 2000, the Danish Lithosphere Centre (DLC) conducted field operations in the area, which offered an opportunity for the retrieval of the drill cores as well as for conducting additional field sampling (Nielsen et al. 2000; Tegner et al. 2009). This development followed year-long debates on the liquid line of descent of the intrusion, the importance of liquid immiscibility and causes of mineralisation. The present study is an outcome of these opportunities and discussions.

The main petrologic interest in the Skaergaard intrusion has traditionally been, and still is, in the crystallisation and solidification modes and the resulting liquid fractionation trend. More recently, interest has shifted towards the precious metal (PGE-Au; where PGE refers to Platinum Group Element) mineralisation, which was discovered around 1990 in the upper part of the intrusion (Bird et al. 1991) and has since been studied by several groups (e.g. Andersen et al. 1998; Nielsen et al. 2015, 2019b; Rudashevsky et al. 2023). The PGE-Au mineralisation occurs within a narrow stratigraphic interval reaching approximately 40 m in the centre of the upper part of the LS. Given that the mineralisation itself had no resolvable influence on the crystallisation trends for the major element and the trace elements of concern in this study, we do not discuss this aspect of the intrusion further. Instead, we encourage interested readers to consult the papers cited above.

This study presents the petrographic and petrological results of the detailed sampling (Fig. 3) of the central profile of the LS based on mineral exploration drill cores and surface samples precisely located using the global positioning system (GPS; Tegner et al. 2009) together with new and improved geological (McBirney 1989b) and topographic maps and aerial photos (see Supplementary Files S6–S8). Our composite profile includes sampling at an average interval of 16 m for a total of 136 samples (Fig. 3D). This spacing provides better resolution than previously possible for the petrography, mineral zone divisions, mineral chemistry, density relations, bulk-gabbro compositions (major, minor and trace elements) and their petrologic implications and bearings on the crystallisation of the parental magma. The field relations and internal rhythmic modal-layering structures of the intrusion have been discussed in detail in the original descriptions (Wager & Deer 1939; Wager & Brown 1967) and several subsequent studies (Maaløe 1978; McBirney & Noyes 1979; Naslund & McBirney 1996; Boudreau & McBirney 1997; Irvine et al. 1998; Nielsen 2004) and so need only brief mentioning in the context of this petrographical study.

3 Methods

This Chapter briefly summarises the methods of the study, including sampling and construction of the reference column and the analytical techniques. Details can be found in the accompanying Appendix 2 (sampling) and Appendix 3 (analytical methods) as well as in previous papers that used the results of this study (Thy et al. 2009a, b; Tegner et al. 2009). The bulk gabbro, major element analyses used in this paper were also partly included, together with some trace elements, in a study of the trapped melt content by Tegner et al. (2009). The complete data set, together with other available Skaergaard analyses, are included in Tegner et al. (2023). Subsets of the samples were also used in isotope studies by Hagen-Peter et al. (2019; Sr) and Lesher et al (2023; Fe).

The new composite profile (Fig. 3) was first described in Tegner et al. (2009). It was constructed using a mineral exploration drill core penetrating the Upper Zone (UZ; Figs 3C, D) from the lower part of UZc and into the upper 100 m of the Middle Zone (MZ). This core section was supplemented by surface samples (Figs 3A, B), extending the coverage of the LS into the Lower Zone (LZ) and the UZc, including the SH and the adjoining part of the UBS. The UBS is not a part of this study. The 51 representative core samples used in the study (Fig. 3C) were sampled in 1993 from Platinova core 90-22 and represent 1052 m of mostly UZ gabbros (Watts, Griffis & McOuat Ltd. 1991; Andersen 1996; Tegner 1997; Andersen et al. 1998). The full drill core, together with other similar cores, have now become available for research purposes at the Natural History Museum of Denmark (Nielsen et al. 2000; Hanghøj 2005).

A total of 85 surface samples were collected in 2000 from profiles largely paralleling the original sampling of Wager & Deer (1939). The surface samples were located using GPS with the purpose of extending the stratigraphic coverage of the drill core samples into the lower and the upper parts of the intrusion. These two sets of samples were used to construct the combined stratigraphic column with an average sample interval of about 16 m (Tegner et al. 2009). The locations of the current samples and drill core are summarised in Fig. 3B, together with the locations of the samples used by Wager & Deer (1939) and Wager & Brown (1967).

The zone boundaries in the stratigraphic column established in this study are based on field sampling and petrographic observations, and largely confirm the zone boundaries mapped by McBirney (1989b) to within the resolution in the constructed composite profile of Fig. 3D. This is particularly the case for the appearances of abundant pyroxene (LZb) and FeTi oxides (LZc), but marginally so for zone boundaries that rely on petrographic interpretations, like MZ and UZ. However, significant differences exist in the relative thicknesses of some zones and subzones compared to those defined by previous results by McBirney (1989a) and Wager & Brown (1967; Fig. 2B). Most prominent is a reduced thickness for MZ that can, at least in part, be ascribed to the improved positioning of samples and zone boundaries by GPS. The thicknesses obtained in this study apply to the established central profile but may not apply to averages for the intrusion as a whole or to marginal positions (Wager & Deer 1939; Nielsen 2004). The differences in the various estimates are probably caused by the bowl-shaped zones that may result in an increased average thickness of the MZ compared to the present estimates for the central part of the intrusion (Irvine 1991; Nielsen 2004).

With knowledge of the absolute volume relations of the zones and subzones and their corresponding stratigraphic height (H, in m), fraction of remining melt (F) can be predicted as a function of H. The subzone volumes and their mass equivalents were reported by Nielsen (2004). A conversion of H to F for the composite profile was proposed by Tegner et al. (2009) using a second-order polynomial equation as:

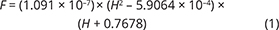
with the result that F = 0.76 at H = 0 m, corresponding to the base of LZa in the composite profile. Further, Eq. (1) predicts that F = 1 at 368 m below LZa, or at the base of the intrusion (HZ) and are used as the baseline for forward modelling in this study. Tegner et al. (2009) assumed that F = 0 at the top of the UZc, corresponding to a height of 2165 m in the composite profile. We also adopt this constraint in our models, although it is not required that the melt will be exhausted on solidification of the LS. Values for F for each sample of the composite profile are shown in Appendix 2.

Samples were ground to a fine powder using either corundum (surface samples) or tungsten-carbide (drill-core samples) shatter boxes. For the tungsten-carbide shatter box, significant contamination was only observed for tungsten. Loss on ignition (LOI) was determined at 950°C and the ferrous-ferric ratios were determined by titration. Major elements and selected trace elements were determined by X-ray fluorescence (XRF) methods using a PANalytical PW2400 X-ray spectrometer at Aarhus University and fused glass (major elements) and powder (trace elements) pellets. The precision (per cent relative standard deviation, %RSD) is typically below 1–2% for major elements, 2–4% for minor elements and 1–9% for trace elements.

Trace element abundances were determined by inductively coupled plasma mass spectrometry (ICP-MS) using an Agilent 7500 instrument at University of California, Davis. Precision was evaluated using multiple analyses of reference standards to be well below 6% for most elements. Bulk-rock specific density was determined by weighing the dry and clean samples in air and in water with an estimated precision 1–2% (Tegner et al. 2009).

The mineralogy and texture of both surface and drill-core samples were characterised by optical microscopy. Throughout this paper, orthopyroxene refers to low-Ca pyroxenes, regardless of whether they precipitated directly as an orthorhombic pyroxene, as may have been the case in the lowermost parts of the intrusion (Wager & Brown 1967; Nwe 1976) or formed from inversion of monoclinic pigeonite. Clinopyroxene (Cpx) refers to monoclinic calcic and subcalcic pyroxenes (Poldervaart & Hess 1951). Ferrobustamite refers to a pyroxenoid phase that is believed to have been formed by inversion from ferrowollastonite (Brown & Vincent 1963) resulting in a mosaic of small grains (Naslund 1984). The bustamite phase was previously described as ferrowollastonite (Brown & Vincent 1963).

Mineral compositions were determined by electron microprobe analysis using either CAMECA SX-50 or SX-100 instruments (wavelength dispersive spectrometers, University of California, Davis) or a JEOL 8600 Superprobe instrument (combination of wavelength and energy dispersive spectrometers, Aarhus University). Beam conditions and beam diameters were similar for both laboratories. The beam diameters were either focused to 1–2 µm or defocused or rasterised to a 20–30 µm broad beam to minimise the effects of exsolution in pyroxenes and oxide minerals. An internal pyroxene standard was analysed at both laboratories concurrently as a control and measure of analytical precision and accuracy. Except for a few pyroxene batches, no inter-laboratory corrections were needed. Precision was estimated to be below 1% for SiO₂, MgO and CaO; below 8% for Al₂O₃, FeO, Na₂O and K₂O and below 20% for TiO₂ and MnO. The analyses of apatite included F (fluorine) and Cl, but with OH calculated by balance.

Modal proportions on a weight basis of the constituent minerals were calculated by weighted, least squares, linear approximations using the mineral and the bulk-rock compositions. Phases considered in the calculations are olivine, plagioclase, clinopyroxene, orthopyroxene, ilmenite, magnetite and apatite for the entire LS with orthoclase and quartz included for the UZ. Only acceptable positive solutions to the least squares approximations were compiled with residual sum of squares typically below 0.1. Because the average mineral compositions used for the modal calculations represent core compositions, the obtained modal results may be biased by not fully representing late-stage crystallised mineral. Such an effect, however, is considered minimal because of the mostly low content of interstitial minerals and because these often are relatively similar to core primocrysts, except in extreme cases of zoning.

4 Stratigraphy of the Layered Series (LS)

4.1 Petrography and zonal division

It is customary to refer to the gabbros of the Skaergaard intrusion and other layered intrusions as cumulates based on cumulus (or primocryst) mineral assemblages. A consequence is that their interpreted primocryst assemblages classify such gabbros without including an often-large amount of minerals crystallised from an interstitial melt component. A further complication with the cumulus and cumulate terminology is that traditionally it has involved genetic assumptions of gravitative or flow accumulations of cumulus minerals in a host silicate melt (Wager & Brown 1967). To avoid such genetic interpretation at the onset of this study, we refer to the gabbros as made up of primocrysts and interstitial material, irrespective of mode of formation.

The most obvious challenge to the cumulus terminology for Skaergaard is that the lowermost gabbros will be classified as troctolite cumulates based on the presence of primocryst plagioclase and olivine, despite them being gabbros or gabbronorites, containing significant amounts of pyroxenes originating from an interstitial melt. During this study of a large number of gabbros, we found it to be impractical to identify the mineral textures as either primocryst or interstitial. For this reason, and to avoid often-subjective interpretations of textures, we use the calculated mineral modes of the bulk compositions to classify the gabbros in accordance with the recommendations of International Union of Geological Sciences (IUGS) Subcommission on the Systematics of Igneous Rocks (Le Maitre 1989). By doing so, we conform to the original practice of Wager & Deer (1939) of classifying the rocks by bulk-mineral modes. One consequence of this practice is that our classification tends to be biased towards the near-solidus phase assemblage rather than the subliquidus assemblage, which in practice elevates the abundance of clinopyroxene and orthopyroxene that are subject to subsolidus exsolution and coarsening as a function of cooling. Like the modal-based classifications, the CIPW normative compositions calculated from the bulk rocks are predominantly olivine-hypersthene normative. The only exception is the upper part of UZc, where quartz-normative compositions (4–10% quartz) prevail due to a high content of interstitial granophyre. Further, for convenience we refer to all clinopyroxene- and plagioclase-bearing rocks as gabbros, despite the fact that from MZ and up they are strictly diorites, given that the An content of plagioclase falls below 50% (Le Maitre 1989). The examined gabbros from the drill core or the field were intended to represent average gabbros. For this reason, we do not use modifying prefixes, such as leuco and melano.

For descriptive purposes, we retain the traditional zonal division based on the predominant primocryst mineralogy of Wager & Deer (1939), Wager & Brown (1967) and McBirney (1989a, b, 1996), but prefer the term primocryst instead of cumulus as advocated by Maaløe (1976a). The LZ is thus characterised by plagioclase, olivine and clinopyroxene; the MZ by plagioclase and clinopyroxene, concurrent with reduction in olivine; and the Upper Zone (UZ) by plagioclase and clinopyroxene, while olivine reappears. Subzones are further defined by abundant and textural change of clinopyroxene from an interstitial habit to a more dominating granular habit (LZb), FeTi oxide minerals composed of an intergrowth of ilmenite and magnetite (LZc), euhedral apatite (UZb) and a mosaic intergrowth of green ferrohedenbergite grains interpreted to have inverted from ferrobustamite (UZc). Orthopyroxene is present in all zones and subzones, including the MZ and into the lower part of UZb.

Minerals in trace amounts as well as late-stage magmatic, hydrothermal and metamorphic minerals (e.g. hydrous minerals and sulphides) are not considered in the present discussion (e.g. Wager et al. 1957; Wager & Brown 1967; Bird et al. 1986, 1988; Manning & Bird 1986; Rudashevsky et al. 2004, 2023; Cabri et al. 2005; Nielsen et al. 2015, 2019b).

We begin by reviewing the petrography of the LS gabbros, as it bears on the zone and subzone divisions of the intrusion, and then consider the stratigraphic variations. Fig. 4 provides an overview of modal compositions illustrating the elevated olivine and apatite contents of UZb and UZc and the FeTi oxide content for much of LZc. Zonal averages are provided in Table 1. Representative plane-polarised, transmitted, microscope images of thin sections of the investigated gabbro samples are given in Supplementary Files S4.

Table 1 Average modal makeup of zones and subzones of the LS (wt%)

Zone	Pl	Ol	Cpx	Opx	Il	Mt	Ap	Q	Kfs
UZc	33.3	19.7	33.8		4.6		1.5	5.4	2.6
UZb	41.3	23.5	21.6		6.6	2.7	4.4
UZa	43.9	7.3	34.1	3.5	8.3	4.7	0.2
MZ	39.7	1.9	33.7	5.9	13.5	5.6	0.1
LZc	34.0	5.5	30.4	7.3	17.1	6.7	0.2
LZb	51.1	4.9	28.0	12.7	2.2	2.3	0.3
LZa	56.1	9.4	13.0	18.0	2.2	1.1	1.1
Pl: plagioclase. Ol: olivine. Cpx: high-Ca pyroxene. Opx: low-Ca pyroxene. Il: ilmenite. Mt: magnetite. Ap: apatite; Q: quartz. Kfs: K-feldspar. Complete data set supplied in Supplementary File S1.

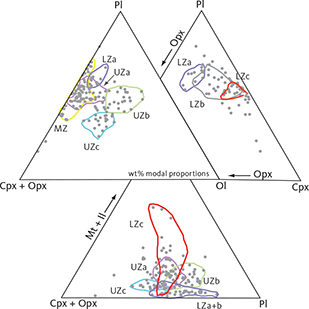
Fig. 4 Summary of calculated modal mineralogy of the examined gabbros displayed in the triangular (Cpx + Opx) – Pl – Ol, Opx – Pl – Cpx (only LZ) and (Cpx + Opx) – (Mt + Il) – Pl diagrams (wt%) with main groupings outlined. Cpx: clinopyroxene. Pl: plagioclase. Ol: olivine. Opx: orthopyroxene. Mt: magnetite. Il: ilmenite. Other abbreviations in Fig. 2.

4.1.1 Lower Zone (LZ)

The LZ comprises 876 m of stratigraphy within the composite profile (Fig. 3) that consist predominantly of gabbronorite (Fig. 4) characterised by plagioclase, olivine, clinopyroxene, orthopyroxene and FeTi oxides. The LZ has been subdivided into three subzones (LZa, LZb and LZc; Fig. 3). The 1966 Cambridge Drill Core I was located in the stratigraphically lowest part of LZb and penetrated through the LZa and 150 m into the HZ to a total stratigraphic thickness of 1026 m (Maaløe 1976a; Holness et al. 2015). Wager & Deer (1939) referred to the gabbros of the LZ as “hypersthene-olivine-gabbros” of which the gabbros in the lower-most part (LZa) were identified as being made up of “transitional rocks” in the sense that they transitioned into the border group.

4.1.1.1 Lower (Sub)Zone a (LZa)

The LZa includes 174 m of olivine gabbronorites (Fig. 3) exposed at the surface and c. 150 m into the subsurface as documented in Cambridge Drill Core I (Maaløe 1976a; Nwe 1976; Holness et al. 2015). On average, LZa has 56 wt% plagioclase, 9 wt% olivine, 13 wt% clinopyroxene and 18 wt% orthopyroxene (Table 1; Figs 4, 5) and contains medium-grained (2–6 mm) primocrysts of plagioclase and olivine predominantly forming a granular network in which olivine tends to be rounded to subhedral and plagioclase tabular in a random to orientated fabric. Ilmenite, magnetite and apatite occur interstitially and rarely exceed a total of 4 wt% (Fig. 6). Biotite is rare and often intergrown with apatite or associated with FeTi oxides. Orthopyroxene occurs as coronas between FeTi oxides and olivine or plagioclase (Fig. 6; Haselton & Nash 1975; Holness et al. 2007a, b). Plagioclase is strongly twinned and displays complex normal and polysynthetic twinning in the lower part of LZa, becoming more homogeneous higher in the stratigraphy (Wager & Brown 1967; Maaløe 1976a; Humphreys 2009; Namur et al. 2014). Plagioclase primocrysts also occur as small (<1 mm) chadacrystic grains in large oikocrystic clinopyroxene.

Fig. 5 Representative petrography of the LZ gabbros (samples 458287, 875 m; 458205, 592 m; 458211, 7 m). Shown are macrophotographs of typical gabbros for each of the three subzones (LZa, b and c). Cpx: Ca-rich pyroxene (with subordinate intergrown low-Ca pyroxene). Mi: mica. Ol: olivine. Opx: low-Ca pyroxene (with subordinate intergrown high-Ca pyroxene). Ox: FeTi oxides (intergrowth of ilmenite and magnetite). Pl: plagioclase. Scale bars are 2 mm.

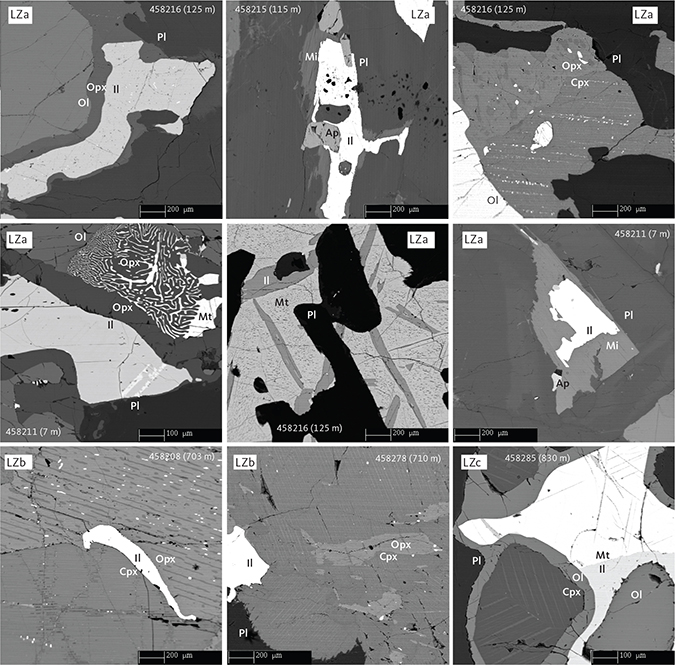
Fig. 6 Representative pyroxene intergrowths and late crystallising mineralogy and textures in LZ gabbros illustrated by backscattered electron (BSE) images. Samples shown in order of appearance: 458216 (125 m), 458215 (115 m), 458211 (7 m), 458208 (703 m), 458278 (710 m), and 458285 (830 m). Ap: apatite. Il: ilmenite. Mt: magnetite. Scale bars are 200 μm or 100 μm, as shown. Other abbreviations in Fig. 5.

4.1.1.2 Lower (Sub)Zone b (LZb)

The LZb comprises 542 m of gabbronorites (Fig. 3) containing on average 51 wt% plagioclase, 5 wt% olivine, 28 wt% clinopyroxene and 13 wt% orthopyroxene (Table 1; Figs 4, 5). Ilmenite, magnetite and apatite are found in minor amounts totalling about 5 wt% and exhibiting textural relationships similar to those observed for LZa. Biotite is a rare accessory phase. The gabbronorites are medium grained to coarse grained (3–8 mm) with primocrysts of plagioclase and olivine. The relationships between the two pyroxenes are similar to those observed in LZa (Fig. 6). The principal difference from LZa is that clinopyroxene predominantly appears as granular, inclusion-free grains and is thus defined as a primocryst and the number of oikocrysts is consequently reduced (Wager & Brown 1967; Holness et al. 2015). We also noticed that the modal abundance of clinopyroxene is higher and olivine lower than in LZa (Table 1; Fig. 4). Orthopyroxene forms coronas between olivine, plagioclase and FeTi oxides, most noticeably in the lower 250 m of the subdivision. The top of LZb is easily defined by the transitional appearance of FeTi oxide-rich layers at the base of LZc.

4.1.1.3 Lower (Sub)Zone c (LZc)

The LZc is represented by 160 m of FeTi oxide gabbronorites (Fig. 3) comprising on average 34 wt% plagioclase, 6 wt% olivine, 30 wt% clinopyroxene, 7 wt% orthopyroxene, 17 wt% ilmenite, 7 wt% magnetite and trace amounts of apatite (Table 1; Figs 4, 5). Overall, the rocks are medium grained (1–5 mm), and finer grained than the LZb, with primocrysts of plagioclase, pyroxenes, olivine and FeTi oxides in a dominating granular texture. The relationships between the two pyroxenes are similar to those observed in LZa (Fig. 6). Reactive coronas of olivine between plagioclase, pyroxene or FeTi oxides are occasionally present instead of the orthopyroxene coronas of LZa to LZb. Locally, the FeTi oxide mode can reach 50 wt% with ilmenite consistently twice as abundant as magnetite (Thy et al. 2009a) and occurring as isolated grains or as intergrowths associated with late-stage oxidation and exsolution (Fig. 6). These lamellar intergrowths occasionally include needles of hercynitic spinel.

4.1.2 Middle Zone (MZ)

The MZ comprises 260 m of the composite profile. It is an FeTi oxide gabbronorite (Fig. 3) containing on average 40 wt% plagioclase, 2 wt% olivine, 34 wt% clinopyroxene, 6 wt% orthopyroxene, 14 wt% ilmenite and 6 wt% magnetite (Table 1; Figs 4, 7). Again, apatite is a trace mineral (≤0.1 wt%). The MZ gabbros are medium grained (2–6 mm) with primocrysts of plagioclase, pyroxenes, olivine and FeTi oxides and have a granular texture. The textural relationship of clinopyroxene and orthopyroxene is similar to that found in LZ (Figs 6, 8), while Fig. 9 shows a clear antithetical relationship between the abundances of olivine and orthopyroxene. Large olivine grains appear abundantly in about 30% of the sampled gabbros throughout the sequence, but particularly in the middle of the MZ at 1010–1025 m depth. Ilmenite and magnetite intergrowths are similar to those described for the LZc. Orthopyroxene coronas are rare and only found at the base of the zone, while olivine coronas are found throughout MZ (Fig. 8); in both cases, the coronas are texturally similar to those found in the LZ. Symplectite intergrowths of plagioclase, olivine, and clinopyroxene, as described by Holness et al. (2011), are present in the upper part of the MZ (Fig. 8; 1055–1060 m in the composite profile).

Fig. 7 Representative petrography of the MZ gabbros (samples 458251, 953 m and 458250, 935 m). Shown are macrophotographs of typical gabbros. Abbreviations in Fig. 5. Scale bars are 2 mm.

Fig. 8 Representative pyroxene intergrowths and late crystallising mineralogy and textures in the MZ gabbros illustrated by BSE images. Samples shown in order of appearance: 458249 (930 m), 458254 (988 m), 458262 (1053 m), 458258 (1009 m), 458259 (1010 m) and 458263 (1055 m). Abbreviations in Figs 5, 6. The pyroxene intergrowth and lamellae are indicated by the grey shading of the images. Scale bars are 200 mm or 100 mm, as shown.

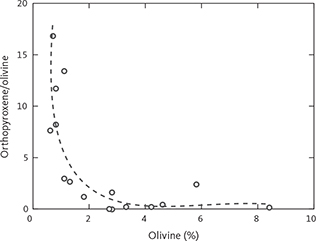
Fig. 9 Antithetic relationship between the calculated modal contents of olivine and orthopyroxene shown as orthopyroxene/olivine (weight ratio) as a function of olivine (wt%) for observations where the modal content of olivine is above zero.

Platinova Resources Ltd. obtained several drill cores during 1986–1990, mostly starting in the UZ and focusing on the potentials for precious metal deposits as part of the so-called Triple Group in the upper part of the MZ. The drill core through the c. 100 m thick mineralised group in the uppermost part of the MZ was not included in this study, although partially covered by surface samples. Petrographic and mineralogical details, including the silicates and FeTi oxides, of this short Triple Group interval have been documented by Andersen (1996, 2006), Andersen et al. (1998) and Nielsen et al. (2005, 2015, 2019b).

4.1.3 Upper Zone (UZ)

The UZ varies from gabbronorite in the lower part to gabbro in the upper part, characterised throughout by plagioclase, olivine, orthopyroxene (disappears at 1600 m height), clinopyroxene and FeTi oxides. The UZ represents 987 m of stratigraphy in the composite profile and has been divided into three subzones (UZa, UZb and UZc; Fig. 3). Wager & Deer (1939) referred to the UZ as “ferro-gabbros” made up of a lower part of “hortonolite” (Fa_50–70), a middle part of “ferro-hortonolite” (Fa_70–80) and an upper part of “fayalite” (Fa_80–100),based on the then common names for the fayalite-content of olivine solid solutions. The UZc was referred to by Wager & Deer (1939) as the “Purple Band” because of the purple-brown weathering that coincides with the appearance of high iron and manganese pyroxene (ferrobustamite).

4.1.3.1 Upper (Sub)Zone a (UZa)

The UZa makes up 432 m of FeTi oxide gabbronorite (Fig. 3) containing on average 44 wt% plagioclase, 7 wt% olivine, 34 wt% clinopyroxene, 4 wt% orthopyroxene, 8 wt% ilmenite, 5 wt% magnetite and c. 0.2 wt% apatite (Table 1; Figs 4, 10). The UZa gabbronorites are medium-grained (1–5 mm) with primocrysts of plagioclase, pyroxenes, olivine and FeTi oxides in a mostly granular texture. Throughout the subzone, olivine modes are markedly higher than in the MZ, while orthopyroxene is relatively rare compared to MZ. The textural relationships between the pyroxenes are, however, similar to those observed for MZ (Figs 8, 11). Olivine coronas between plagioclase, pyroxene and FeTi oxides are present, but rare, while FeTi oxides are found as isolated grains or intergrown with silicate minerals.

Fig. 10 Representative petrography of UZ gabbros (samples 458653, 2075 m; 90-22-344.1, 1748 m and 90-22-854.5, 1237 m). Shown are macrophotographs (transmitted light) of typical gabbros for each of the three subzones (UZa, b and c). Abbreviations in Figs 5, 6. Scale bars are 2 mm for all photographs.

Fig. 11 Representative pyroxene intergrowths and late crystallising mineralogy and textures in UZa and UZb gabbros illustrated in BSE images. Samples shown in order of appearance: 90-22-854.5 (1237 m), 90-22-809.2 (1282 m), 90-22-290.8 (1801 m) and 90-22-461.8 (1630 m). Abbreviations in Figs 5, 6. Scale bars are 200 mm or 100 mm, as shown.

4.1.3.2 Upper (Sub)Zone b (UZb)

The UZb consists of 424 m of FeTi oxide and apatite gabbro (Fig. 3) with an average of 40 wt% plagioclase, 24 wt% olivine, 22 wt% clinopyroxene, 7 wt% ilmenite, 3 wt% magnetite, and 4 wt% apatite (Table 1; Figs 4 and 10). The gabbros are medium grained to coarse grained (2–8 mm) with primocrysts of plagioclase, clinopyroxenes, olivine, FeTi oxides and apatite in a mostly granular texture. Orthopyroxene is occasionally found (e.g. at 1630 m; Fig. 11). The most conspicuous features of UZb are the high olivine mode, the near absence of orthopyroxene and the occurrence of abundant apatite, the latter used to define the base of this subzone. Up-section, hedenbergite becomes distinctly brown and pleochroic, while olivine is commonly oxidised. Coronas of olivine are rare, but otherwise textures are similar to those in UZa.

4.1.3.3 Upper (Sub)Zone c (UZc)

The UZc comprises 123 m of chiefly ferrograbbros, or more precisely ferrodiorites (Fig. 3), with an average of 33 wt% plagioclase, 20 wt% olivine, 34 wt% clinopyroxene, 5 wt% ilmenite, 2 wt% apatite, 5 wt% quartz, and 1 wt% orthoclase (Table 1; Figs 4, 10). Magnetite is scarce or absent. Quartz appears as individual grains or in conspicuous granophyric intergrowth with orthoclase, albite and quartz; the latter is thought to have inverted from tridymite (Lindsley et al. 1969; Larsen & Tegner 2006). The base of UZc is defined by a change from granular hedenbergite to a fine-grained interlocking mosaic of green ferrohedenbergite with high manganese and brown ferrohedenbergite with low manganese and high titanium (Fig. 12). The green ferrohedenbergite is interpreted as inverted from ferrobustamite, while the brown ferrohedenbergite is thought to have crystallised directly from a late silicate melt (Naslund 1984). This mosaic pyroxene texture is shown in Fig. 10 (transmitted light) and Fig. 11 (backscattered electron (BSE) image). The UZc gabbro also contains abundant interstitial granophyre or micropegmatite that increases up-section, reaching up to 14 wt% of the rock composed of a granophyric intergrowth of quartz, albite and orthoclase (Figs 13, 14). Orthoclase is confined to graphic intergrowths, while quartz and albite also occur as rare granular grains.

Fig. 12 Mineralogy and textures of ferrohedenbergite and inverted ferrobustamite intergrowths in a UZc gabbro (sample 458643, 2150 m) illustrated in a BSE density image and elemental-mapped electron Kα images (Mn and Ti). Other abbreviations in Figs 5, 6. The relationship between the two pyroxenes is seen as green inverted ferrobustamite, characterised by a mosaic of grains, rimmed by a late crystallising brownish ferrohedenbergite. Scale bars are 1000 mm.

Fig. 13 Elemental-mapped electron Kα images (Si, Na, K, Al) of interstitial granophyre patches in UZc (sample 458643, 2150 m). Intergrown albite (An_~0), quartz and orthoclase are seen along margins of trapped plagioclase grain (An_~25-30). Pl: plagioclase. Px: pyroxenes. Q: quartz. Ox: FeTi oxides. Scale bars are 1000 μm.

Fig. 14 Textures of melanogranophyre from UZc (458643, 2150 m) illustrated by a BSE density image. The sample is composed of granular albitic plagioclase (~An₂₅–₃₀), pyroxenes (see Fig. 11), olivine and interstitial granophyre (see Fig. 13). Pl: plagioclase. Px: pyroxenes. Ol: olivine. Q: quartz. Ox: FeTi oxides (mostly ilmenite). Scale bar is 10 mm.

4.1.4 Liquid immiscibility

Jakobsen et al. (2005) and Jakobsen (2007) presented evidence for liquid immiscibility by examining mineral inclusions in the same set of samples analysed as part of the present study. After homogenising these inclusions, they were able to identify coexisting silica-rich and silica-poor inclusions in apatite and olivine of the UZb and UZc and interpreted these as conjugate immiscible melts. In a more extensive study, Jakobsen et al. (2011) showed that melt inclusions trapped in early-crystallised plagioclase could be detected as early as in the upper part of the LZ. They suggested that these represented entrapment of variable amounts of two conjugate immiscible melts in an evolving interstitial melt and that the upper part of the LS from about LZc, through MZ and UZ, crystallised from an emulsion of immiscible melts.

4.2 Mineral mode and variation in gabbro density

The mineral modes shown in Fig. 15 and summarised in Table 2 are calculated from bulk-gabbro compositions and the mineral compositions present in the individual gabbro samples. Thus, the modes represent solidus or subsolidus conditions and not necessarily liquidus or subliquidus conditions. Despite such limitations, several of the features revealed, contribute to our understanding of liquidus conditions.

Table 2 Summary of calculated modes without trapped melt

Zone	Stratigraphic height (m)		F	Ol	Opx	Cpx	Pl	Mt	Il	Ap	Q	Kfs
	high	low		(wt%)	(wt%)	(wt%)	(wt%)	(wt%)	(wt%)	(wt%)	(wt%)	(wt%)
UBS	2169	2165		17.17		22.97	40.80		3.70	1.37	9.10	4.90
UZc	2165	2165	0.000	19.59		27.86	37.79		3.53	0.87	7.06	3.30
UZc	2165	2164	0.000	21.13		32.69	28.92		5.10	1.60	7.10	3.47
UZc	2163	2147	0.001	19.67		32.94	31.55		4.77	1.47	6.84	2.77
UZc	2144	2141	0.003	22.70		36.63	26.27		4.83	1.80	5.50	2.27
UZc	2091	2081	0.010	15.87		42.63	33.40		5.13	1.80	0.83	0.33
UZc	2075	2060	0.012	20.71		40.07	30.44		5.34	1.87	1.00	0.57
UZc	2060	2046	0.014	21.10		34.78	37.68		4.50	1.23	0.44	0.27
UZb	2044	2030	0.016	19.97		24.37	38.97		3.64	1.10	11.35	0.60
UZb	2024	1984	0.019	22.33		30.33	40.07	0.43	4.83	2.00
UZb	1962	1921	0.029	24.02		24.42	42.97	0.17	5.50	2.93
UZb	1902	1862	0.039	22.67		19.17	47.68	0.97	6.00	3.50
UZb	1843	1801	0.050	24.14		19.96	40.86	4.03	6.73	4.28
UZb	1782	1748	0.062	26.20		19.50	41.03	0.67	7.77	4.83
UZb	1728	1691	0.073	27.34		13.36	38.67	3.66	9.37	7.61
UZb	1671	1630	0.085	20.68		21.84	40.55	2.97	7.27	6.70
UZb	1620	1600	0.097	10.86		33.58	40.04	5.54	6.93	3.05
UZa	1561	1527	0.112	8.09	4.94	26.94	48.80	3.17	7.93	0.13
UZa	1506	1431	0.126	9.11	0.84	32.04	45.95	2.56	9.44	0.07
UZa	1403	1343	0.154	6.72	3.72	30.92	46.21	3.80	8.47	0.17
UZa	1323	1282	0.177	11.82		32.60	41.79	5.13	8.16	0.50
UZa	1268	1237	0.194	7.42	0.07	36.77	41.47	6.85	7.29	0.13
UZa	1218	1188	0.210	3.96	1.30	39.66	42.02	3.19	9.66	0.20
UZa	1178	1131	0.223	1.57	3.98	37.58	41.22	6.61	8.91	0.13
MZ	1098	1055	0.251	0.23	8.31	25.39	46.82	4.49	14.66	0.10
MZ	1053	1032	0.267	0.00	8.78	39.12	32.56	0.89	18.65	0.00
MZ	1024	1009	0.277	3.47	8.04	35.57	37.25	5.53	10.07	0.07
MZ	1003	1002	0.285	0.87	4.95	30.62	42.73	8.12	12.66	0.07
MZ	988	961	0.291	4.17	3.93	42.60	27.08	4.01	18.11	0.10
MZ	953	930	0.304	2.03	2.89	31.97	37.04	10.79	15.22	0.06
MZ	921	900	0.316	1.74	6.13	28.54	49.28	4.48	9.76	0.07
MZ	890	875	0.329	3.86	0.03	30.59	42.59	7.08	15.77	0.07
LZc	847	816	0.346	6.15	2.98	27.85	30.17	10.36	21.97	0.53
LZc	808	798	0.362	5.45	2.74	23.74	31.74	6.88	29.23	0.22
LZc	784	742	0.372	2.08	7.44	43.12	34.19	4.49	8.59	0.10
LZc	723	703	0.398	6.61	8.73	34.26	46.49	1.78	2.00	0.13
LZb	703	681	0.406	4.86	11.94	27.45	50.94	1.51	2.60	0.69
LZb	634	580	0.437	3.49	8.82	33.36	51.78	0.40	1.76	0.40
LZb	558	488	0.472	9.12	11.72	27.68	49.11	0.26	1.95	0.16
LZb	447	367	0.526	6.54	15.07	23.37	52.53	0.45	1.90	0.13
LZb	346	221	0.576	2.76	14.72	25.17	50.39	4.55	2.31	0.11
LZb	177	173	0.667	3.60	16.72	16.80	60.00	0.38	2.30	0.19
LZa	161	137	0.676	7.95	16.59	14.57	57.37	1.20	2.03	0.30
LZa	125	107	0.696	10.84	22.63	10.84	51.39	1.40	2.57	0.33
LZa	96	27	0.712	13.54	16.99	13.66	52.70	0.66	2.13	0.31
LZa	7		0.764	7.11	17.22	18.32	53.65	1.30	2.10	0.30
Calculated modes normalised to a total gabbro mode of 100%. Each determination is based on three samples, except at 7 m where only one sample was used. Compare to Table 24 for the same modes given with preferred trapped-melt content. The high quartz content at the top of UZb is caused by a single sample characterised as being a melanogranophyre. F: liquid remaining after Tegner et al. (2009), (Eq.) 1. Complete data set in Supplementary File S1. Ol: olivine. Opx: orthopyroxene. Cpx: clinopyroxene. Pl: plagioclase. Mt: magnitite. Ap: apetite. Q: quartz. Kfs: Orthoclase.

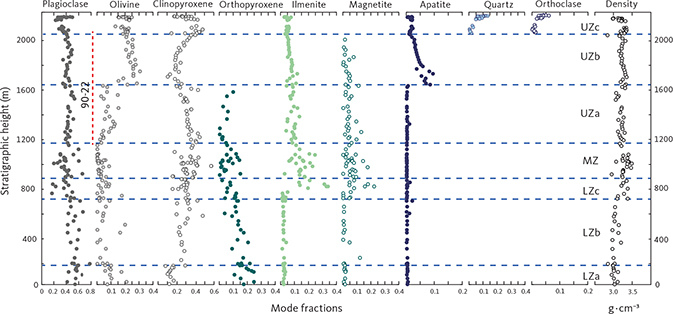
Fig. 15 Modal variation of the LS (as weight fractions) as a function of stratigraphic height (m). Calculated based on bulk-rock and mineral compositions as described in Section 4.2 and Table 2. Shown are plagioclase, olivine, clinopyroxene, orthopyroxene, ilmenite, magnetite, apatite, quartz and orthoclase. Last column is the measured gabbro density (g·cm⁻³) obtained using Archimedes’ principle. Vertical red line: location of drill core 90-22.

Plagioclase is by far the dominant mineral at about 40–60 wt%. The plagioclase content in the LZ is constant at about 50 wt% up to LZc, where a fall in plagioclase modes upwards into MZ is related to the appearance of FeTi oxides. Plagioclase content is then constant until UZc where it drops followed by a sharp increase towards the top of this zone (Fig. 15). The clinopyroxene modes vary between 30 wt% and 50 wt% but are markedly lower in LZa (10–20 wt%), where clinopyroxene is interpreted to be interstitial and thus correlated with the amount of trapped melt. Furthermore, there is a marked decrease in clinopyroxene modes through UZa and into the base of the UZb, replaced by a reversal to increasing modes through the rest of UZb, culminating in a marked increase in UZc followed by a sharp decrease towards the SH.

Olivine is mostly well below 10 wt% from the LZ and until UZb. Remarkably, olivine increases up to 25–30 wt% at the base of UZb, followed by a systematic drop further upward into UZb (Fig. 15). A minor drop in the upper part of MZ is correlated with a corresponding increase in the orthopyroxene content.

Orthopyroxene shows a marked decline upwards from a maximum of 25 wt% in LZa and 5 wt% in the lower part of the MZ. In the middle and upper part of the MZ, an increase in orthopyroxene is correlated with a drop in olivine. Orthopyroxene tapers out in UZa and disappears in UZb.

Both ilmenite and magnetite appear near simultaneously in the base of the LZc and peak in the centre of LZc at about 20 wt% ilmenite and 5 wt% magnetite, despite large modal variations related to layering (Thy et al. 2009a; Tegner et al. 2009). Both oxide modes systematically reduce upwards through the MZ and UZb. Magnetite is virtually absent in the UZc. Apatite shows a strong increase at the base of UZb (Holness et al. 2017b) where it first appears as an early mineral with average rocks containing up to c. 8 wt% and subsequently decreases. Quartz and orthoclase were only detectable in the UZc, where they sharply increase.

There exist few modal data obtained by point counting for Skaergaard gabbros (Maaløe 1987; Conrad & Naslund 1989), probably due to the problem of obtaining reliable information from the coarse-grained rocks. Most of these data are from Maaløe (1974, 1976a, 1978, 1987), obtained for the purpose of understanding the origin of layering at selected intervals in the stratigraphy. Maaløe (1974, 1987) discussed in detail a short interval (a total of c. 4.7 m) in LZa and obtained an average mode of 59 wt% plagioclase, 18 wt% olivine, 14 wt% clinopyroxene, 7 wt% orthopyroxene and 3 wt% FeTi oxides (on a weight basis). Conrad & Naslund (1989) examined three 10–15 cm thick, modally- and size-graded, single gabbroic layers in UZa that showed a strong anti-correlation between olivine and plagioclase, amounting to a doubling in plagioclase and a complete depletion in olivine modes upward in these layers. Taking their data directly from their graphs and recalculating to a weight basis, suggest averages of 41 wt% plagioclase, 32 wt% clinopyroxene, 9 wt% olivine and 18 wt% FeTi oxides. Most of these point-counted modal data for LZa and UZa compare reasonably well with the calculated modal contents of this study (Table 1).

Knowing the absolute amount of modal orthopyroxene is critical for evaluating potential liquid lines of decent, mineral reactions and the parental-magma composition. It is possible that the apparent high orthopyroxene content in LZ may at least in part reflect solidus and subsolidus exsolution from clinopyroxene and may thus not reflect the liquidus content. This may be due to the inability of the electron microprobe analyses to capture the bulk-pyroxene composition despite the broad beam used. Holness et al. (2015) optically mapped thin sections, similar to those examined in this study, and obtained average LZa compositions of 60 wt% plagioclase, 13 wt% olivine, 18 wt% clinopyroxene, 7 wt% orthopyroxene, and 2 wt% FeTi oxides. Both these optical estimates differ from the estimate using least-squares mixing calculations in this study (Table 1), principally by the lower total amount of orthopyroxene as well as a lower proportion of orthopyroxene of the total pyroxenes (0.3 against 0.6). Likewise, the CIPW normative compositions estimate 58 wt% plagioclase, 15 wt% olivine, 12 wt% clinopyroxene, 10 wt% orthopyroxene and 5 wt% FeTi oxides for the LZa gabbro – closer, but not close enough, to the 56 wt% plagioclase, 9 wt% olivine, 13 wt% clinopyroxene, 18 wt% orthopyroxene and 2 wt% FeTi oxides calculated by mixing. These differences are no doubt related to the effects of partial un-mixing and exsolution of the pyroxenes and magnetite on the modes calculated based on subsolidus re-equilibrated gabbros.

The bulk-gabbro density measured by weighing the dry and clean samples in air and in water reflects the modal variation of the gabbros (Fig. 15). The density is constant, around 3.03 ± 0.10 g·cm^–3 in the LZa and LZb, but markedly increases with the appearance of FeTi oxides in the LZc to highly variable values of 3.3 to 4.2 g·cm^–3 with an average of 3.6 g·cm^–3. The UZ starts with a slight decrease upward in UZa, followed by a reversal to higher values in UZb, reflecting the high iron-rich olivine content in these gabbros, and again followed by a slight decrease in the upper parts of the UZb.

4.3 Mineral chemistry

4.3.1 Olivine

Olivine ranges in composition between Fo₆₇ and Fo₀₁, initially with little systematic upward variation in the LZ (LZa Fo_67.0–Fo_48.1; LZb Fo_61.2–Fo_47.4; LZc Fo_60.2–Fo_47.4), followed by a marked and systematic decrease starting in the upper part of the MZ (MZ Fo_51.3–Fo_39.3; UZa Fo_41.7–Fo_25.1; UZb Fo_30.2–Fo_1.8; UZc Fo_4.5–Fo_0.8). Olivine in the HZ reaches Fo content of Fo_66.0 (Nwe 1976; Holness et al. 2013, 2015) and Fo_74.3 in the so-called ‘tranquil division’ of LZa* of MBS (Hoover 1989b).

Table 3 presents average olivine compositions calculated per formula unit (pfu) of four oxygens. Based on 921 analyses acquired in this study, olivine has a near ideal stoichiometry (M₂SiO₄, where M is the total cations Mg, Fe, Mn and Ca) with total cations of 3.010 ± 0.014 (1σ) calculated to a formula unit of 4 oxygens (M_2.02Si_0.99O₄), Si of 0.990 ± 0.014 (1σ), and a strong negative correlation between Mg and Fe (Fe = 2.000 – 0.971 Mg; ∑R² = 0.998) with end points for pure fayalite of 1.999 (Fe+Mn) and for forsterite of 2.060. Manganese systematically increases up-section from 0.011pfu at the base of LZa to 0.051 pfu at the base of the UZc and then decreases to 0.010 pfu (Fig. 16), because of the appearance of Mn-rich ferrobustamite. The average calcium content is 0.10 ± 0.06 (wt% CaO) or 0.003 ± 0.002 (Ca pfu) with no correlation with Mg content. Olivine coronas analysed (n = 11) in rocks of LZc to UZa (Figs 6, 8, 11) are systematically more Fo-rich by 1–3 wt% Fo compared to the primocryst compositions (Fig. 17).

Table 3 Average olivine compositions

Zone	Stratigraphic height (m)		n	SiO2 (wt%)		TiO2 (wt%)		FeO (wt%)		MnO (wt%)		MgO (wt%)		CaO (wt%)		NiO (wt%)		Total (wt%)	Fo
	high	low		Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD		Ave.	SD
UBS	2169	2165	28	28.91	0.248	0.06	0.015	69.50	0.583	0.65	0.091	0.32	0.075	0.36	0.429	0.03	0.021	99.83	0.01	0.002
UZc	2165	2165	13	29.35	0.188	0.09	0.014	70.14	0.737	0.48	0.051	0.04	0.019	0.16	0.175	0.03	0.013	100.28	0.00	0.015
UZc	2165	2164	14	29.87	0.215			70.59	0.421	0.50	0.031	0.09	0.103			0.02	0.019	101.07	0.00	0.003
UZc	2163	2147	23	29.30	0.193			70.12	0.615	0.79	0.080	0.06	0.038			0.02	0.013	100.29	0.00	0.001
UZc	2144	2141	14	28.99	0.439	0.10	0.015	69.77	0.823	1.07	0.095	0.08	0.018	0.14	0.091	0.04	0.019	100.18	0.00	0.000
UZc	2091	2081	20	29.14	0.215			68.42	0.503	1.44	0.071	0.44	0.083			0.03	0.013	99.47	0.01	0.002
UZc	2075	2061	13	29.11	0.268			66.93	0.486	1.64	0.091	0.56	0.063			0.02	0.012	98.27	0.01	0.002
UZc	2060	2046	28	29.37	0.258			67.13	0.617	1.74	0.152	1.03	0.101			0.02	0.017	99.29	0.03	0.003
UZb	2044	2030	15	29.61	0.896	0.09	0.025	68.23	1.957	1.13	0.064	0.19	0.049	0.16	0.058	0.03	0.024	99.44	0.01	0.002
UZb	2024	1984	26	29.89	0.409	0.09	0.010	66.32	0.831	1.37	0.081	2.26	0.111	0.22	0.284	0.02	0.012	100.16	0.06	0.003
UZb	1962	1921	36	30.10	0.353	0.08	0.010	64.64	1.044	1.22	0.068	3.74	0.260	0.09	0.050	0.02	0.015	99.89	0.09	0.006
UZb	1902	1862	24	30.56	0.273			62.12	0.404	1.11	0.041	5.39	0.230			0.02	0.013	99.20	0.13	0.005
UZb	1843	1801	22	30.93	0.269	0.08	0.018	60.96	1.005	0.94	0.063	7.58	0.318	0.08	0.086			100.56	0.18	0.008
UZb	1782	1748	18	31.25	0.312	0.06		58.57	0.590	0.90	0.034	9.47	0.342	0.10				100.34	0.22	0.007
UZb	1728	1691	17	32.07	0.195			55.25	0.562	0.85	0.089	11.57	0.176			0.03	0.017	99.77	0.27	0.003
UZb	1671	1630	60	32.17	0.261			54.22	0.312	0.81	0.079	12.65	0.255			0.04		99.89	0.29	0.005
UZb	1620	1600	18	31.95	0.288			55.74	0.404	0.84	0.059	11.10	0.285			0.01		99.65	0.26	0.005
UZa	1561	1527	27	32.16	0.326			54.58	0.482	0.83	0.057	12.31	0.200					99.89	0.29	0.004
UZa	1506	1431	21	32.36	0.234	0.03	0.021	54.01	0.685	0.79	0.029	13.50	0.260	0.07	0.055	0.05		100.81	0.31	0.006
UZa	1403	1343	23	32.68	0.319	0.04	0.012	51.74	0.594	0.72	0.041	15.41	0.213	0.10	0.036	0.03		100.72	0.35	0.005
UZa	1323	1282	25	33.20	0.204			48.74	0.453	0.73	0.064	17.17	0.289			0.02	0.009	99.86	0.39	0.005
UZa	1268	1237	25	33.18	0.340	0.09		49.53	0.602	0.71	0.069	16.86	0.290			0.08	0.018	100.45	0.38	0.005
UZa	1218	1188	8	32.85	0.227			49.51	0.411	0.69	0.018	16.65	0.388			0.09	0.019	99.80	0.37	0.006
UZa	1178	1131	15	33.04	0.280	0.06		48.32	0.747	0.67	0.036	17.67	0.258	0.06		0.09	0.029	99.91	0.39	0.006
MZ	1098	1055	3	33.70	0.211	0.06	0.038	47.12	0.653	0.52	0.059	20.21	0.327	0.13	0.052	0.04	0.056	101.78	0.43	0.002
MZ	1053	1032
MZ	1024	1009	16	33.42	0.335	0.03	0.022	46.90	0.741	0.59	0.058	20.82	0.249	0.09	0.026	0.06	0.057	101.91	0.44	0.005
MZ	1003	1002
MZ	988	961	21	34.28	0.318	0.05	0.023	43.90	0.705	0.56	0.068	23.28	0.568	0.09	0.027	0.10	0.07	102.27	0.49	0.010
MZ	953	930
MZ	921	900	8	33.51	0.782	0.16	0.021	46.03	1.057	0.55	0.071	21.90	0.071	0.06	0.020	0.05	0.08	102.25	0.46	0.006
MZ	890	875	5	34.34	0.258	0.03	0.025	40.61	1.158	0.52	0.072	23.21	0.916	0.09	0.047	0.10	0.08	98.89	0.50	0.007
LZc	847	816	15	34.92	0.246	0.05	0.026	39.39	1.053	0.50	0.096	25.89	0.618	0.09	0.041	0.03	0.06	100.88	0.54	0.011
LZc	808	798	12	35.27	0.195	0.04	0.034	38.88	0.680	0.44	0.080	26.84	0.466	0.10	0.028	0.10	0.08	101.68	0.55	0.007
LZc	784	742	16	34.77	0.359	0.03	0.020	40.89	0.845	0.47	0.069	25.23	0.315	0.08	0.029	0.08	0.07	101.54	0.52	0.008
LZc	723	703	13	34.64	0.233	0.04	0.029	41.22	0.554	0.48	0.103	25.27	0.309	0.12	0.017	0.09	0.09	101.86	0.52	0.004
LZb	703	681	17	34.40	0.219	0.05	0.049	42.23	0.446	0.48	0.105	25.20	0.266	0.11	0.032	0.07	0.07	102.52	0.52	0.005
LZb	634	580	11	34.35	0.289	0.06	0.025	41.73	0.567	0.52	0.079	23.24	0.168	0.13	0.036	0.08	0.07	100.11	0.50	0.004
LZb	558	488	31	34.82	0.306	0.04	0.025	41.11	0.438	0.50	0.075	25.37	0.379	0.11	0.033	0.08	0.05	102.02	0.52	0.005
LZb	447	367	13	34.70	0.316	0.03	0.023	40.96	0.558	0.43	0.065	26.28	0.338	0.12	0.030	0.10	0.08	102.61	0.53	0.008
LZb	346	221	20	35.31	0.279	0.04	0.027	37.27	0.691	0.43	0.042	27.69	0.444	0.09	0.021	0.09	0.07	100.93	0.57	0.004
LZb	177	173	16	34.63	0.278	0.04	0.030	40.15	0.863	0.51	0.106	25.41	0.269	0.10	0.042	0.08	0.07	100.93	0.53	0.006
LZa	161	137	18	35.28	0.378	0.04	0.015	37.14	0.796	0.46	0.080	27.16	0.280	0.09	0.029	0.08	0.07	100.23	0.57	0.008
LZa	125	96	19	35.32	0.261	0.03	0.017	36.29	0.645	0.47	0.039	28.15	0.339	0.07	0.026	0.14	0.06	100.48	0.58	0.005
LZa	96	27	21	35.37	0.428	0.03	0.025	36.67	1.637	0.48	0.078	27.96	1.131	0.07	0.021	0.10	0.06	100.69	0.57	0.025
LZa	7		6	35.78	0.502	0.04	0.021	34.05	2.735	0.44	0.071	29.99	2.086	0.07	0.023	0.09	0.09	100.45	0.61	0.025
n: number of individual mineral analyses used for each calculated average (Ave.) for three consecutive samples with 1σ SD where n > 2. Stratigraphic height is given as high and low referring to the interval used for averaging. Complete data set in Supplementary File S1. Fo as mole fractions.

Fig. 16 Olivine mineral chemistry showing Mn as a function of Mg as cations per formula unit (pfu) normalised to 4 oxygens (Table 3). The approximate locations of the zone boundaries of the LS are indicated along the top of the graph. Small blue dots: analysed point compositions. Black dots: average compositions for individual thin sections with 1σ standard deviation (SD). Open circles: corona compositions shown in Fig. 17. Ave.: average.

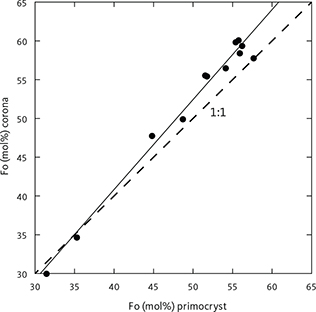
Fig. 17 Composition of olivine coronas (Fo mol%, see Fig. 6) as a function of average primocryst composition (Fo mol%, shown with the 1:1 relationship (dashed line). The linear equation (solid line) is Fo^c = 1.160 Fo^p – 5.589 (∑R² = 0.990, n = 11), where ^c is corona and ^p is primocryst.

The present results are consistent with earlier determinations of olivine compositions made using optical or X-ray methods by analysing mineral separates (Deer & Wager 1939; Wager & Deer 1939; Yoder & Sahama 1957; Wager & Brown 1967) and later by electron microprobe analyses (e.g. Nwe 1976; McBirney 1989a).

4.3.2 Plagioclase

Plagioclase ranges in composition from An₇₂ to An₂₃ with weak systematic upward decreases within LZ (LZa An_71.6–An_51.3; LZb An_62.0–An_47.9; LZc An_57.0–An_45.6) and MZ (An_68.5–An_42.1), and continuing with a more marked decrease in UZ (UZa An_47.9–An_37.7; UZb An_41.1–An_30.2; UZc An_38.2–An_23.4). Plagioclase in the LZa and LZb may show strong normal zoning, and rarely, reverse zoning (Wager & Brown 1967; Maaløe 1976a; Toplis et al. 2008; Namur et al. 2014), reflected here in the uncertainties of the drill-core analyses. While plagioclase in the HZ reaches similar maximum An contents of An_68.9 (Maaløe 1976a; Holness et al. 2013, 2015), it has been recorded in the MBS to reach An_71.4 in the tranquil division of the LZa* (Hoover 1989b). The HZ plagioclase compositions are slightly higher than the maximum values (An_69.5) reported from the UBS by Salmonsen & Tegner (2013). Table 4 shows average plagioclase compositions calculated as pfu of eight oxygens. The composition of plagioclase in the granophyres in UZb and UZc is albitic, ranging from An_4–7 in interstitial granophyres to An_18–27 in pockets of granophyre in pegmatitic gabbro (Larsen & Brooks 1994; Larsen& Tegner 2006). It is thus predictable that a whole range of plagioclase compositions from An₄₀ to An₀ may occur in the granophyres and associated gabbros.

Table 4 Average plagioclase compositions

Zone	Stratigraphic height (m)		n	SiO2 (wt%)		TiO2 (wt%)		Al2O3 (wt%)		FeO (wt%)		MgO (wt%)		CaO (wt%)		Na2O (wt%)		K2O (wt%)		Total (wt%)	An
	high	low		Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD		Ave.	SD
UBS	2169	2165	15	61.43	0.496	0.03	0.020	23.96	0.392	0.36	0.081	0.01	0.004	5.22	0.314	8.54	0.217	0.44	0.093	99.99	0.247	0.016
UZc	2165	2165	15	61.28	0.327	0.04	0.016	24.08	0.235	0.44	0.031	0.01	0.004	5.70	0.227	8.08	0.206	0.56	0.051	100.19	0.272	0.012
UZc	2164	2164	23	60.96	0.479	0.03	0.007	24.01	0.211	0.45	0.161	0.02	0.004	5.93	0.162	7.76	0.202	0.46	0.049	99.62	0.288	0.009
UZc	2163	2147	26	60.92	0.537	0.04	0.014	24.02	0.339	0.43	0.054			5.73	0.277	7.96	0.174	0.54	0.071	99.63	0.274	0.014
UZc	2144	2141	18	60.86	0.474	0.05	0.018	24.32	0.210	0.45	0.050	0.02	0.003	6.11	0.251	7.79	0.143	0.55	0.051	100.15	0.292	0.012
UZc	2091	2081	20	59.75	0.474			24.20	0.358	0.45	0.049			6.64	0.364	7.24	0.159	0.47	0.103	98.75	0.325	0.016
UZc	2075	2061	21	59.13	0.433			24.21	0.194	0.43	0.030			6.63	0.225	7.35	0.170	0.41	0.059	98.17	0.323	0.012
UZc	2060	2046	9	58.90	0.541			24.45	0.278	0.44	0.032	0.01	0.006	6.96	0.253	7.07	0.231	0.41	0.032	98.24	0.342	0.012
UZb	2044	2030	16	59.21	0.442	0.04	0.020	24.82	0.190	0.45	0.036	0.02	0.006	6.47	0.221	7.75	0.171	0.48	0.036	99.25	0.306	0.011
UZb	2024	1984	27	59.30	0.476	0.05		24.79	0.318	0.44	0.027	0.01	0.004	6.91	0.273	6.95	0.158	0.39	0.029	98.85	0.344	0.012
UZb	1962	1921	29	58.58	0.568	0.04		24.87	0.344	0.44	0.025	0.04	0.015	7.08	0.331	6.89	0.271	0.46	0.036	98.40	0.349	0.015
UZb	1902	1862	27	57.82	0.758			25.07	0.316	0.39	0.045			7.22	0.220	6.79	0.143	0.50	0.053	97.78	0.357	0.010
UZb	1843	1801	18	58.36	0.381			25.36	0.152	0.40	0.060			7.50	0.159	6.60	0.181	0.48	0.031	98.71	0.372	0.010
UZb	1782	1748	18	57.66	0.476			25.41	0.183	0.36	0.070			7.49	0.154	6.73	0.159	0.56	0.056	98.22	0.365	0.009
UZb	1728	1691	18	58.15	0.388			25.46	0.176	0.41	0.044			7.70	0.202	6.53	0.144	0.46	0.026	98.71	0.381	0.011
UZb	1671	1630	43	57.54	0.500			25.63	0.215	0.35	0.048			7.74	0.165	6.53	0.131	0.47	0.034	98.26	0.382	0.009
UZb	1620	1600	17	57.73	0.392			25.90	0.264	0.33	0.078			7.92	0.192	6.33	0.194	0.42	0.027	98.63	0.396	0.010
UZa	1561	1527	18	56.51	0.259			26.13	0.196	0.34	0.041			8.34	0.150	6.34	0.184	0.44	0.029	98.10	0.407	0.010
UZa	1506	1431	17	56.30	0.437			26.40	0.234	0.31	0.048			8.63	0.256	6.27	0.176	0.43	0.034	98.33	0.419	0.013
UZa	1403	1343	19	55.97	0.619	0.05		26.69	0.247	0.28	0.039			8.91	0.301	6.10	0.223	0.40	0.052	98.39	0.434	0.014
UZa	1323	1282	19	55.63	0.520			26.76	0.341	0.28	0.054			8.90	0.324	6.07	0.156	0.39	0.034	98.03	0.435	0.015
UZa	1268	1237	9	55.34	0.892			26.82	0.346	0.27	0.026			9.02	0.382	6.02	0.288	0.44	0.049	97.90	0.439	0.021
UZa	1218	1188	26	55.33	0.814			26.70	0.387	0.26	0.027			8.89	0.413	5.89	0.187	0.44	0.039	97.50	0.440	0.017
UZa	1178	1131	24	55.54	0.675	0.09	0.027	26.96	0.336	0.30	0.057	0.03	0.013	9.15	0.265	6.05	0.197	0.40	0.023	98.52	0.443	0.014
MZ	1098	1055	16	55.62	0.642	0.09	0.020	27.73	0.314	0.38	0.142	0.03	0.017	9.63	0.310	6.25	0.197	0.35	0.034	100.09	0.451	0.012
MZ	1053	1032	12	54.33	0.638	0.11	0.025	27.57	0.381	0.41	0.097	0.03	0.022	9.92	0.398	6.16	0.163	0.28	0.061	98.81	0.464	0.017
MZ	1024	1009	23	54.78	0.532	0.10	0.027	27.72	0.367	0.37	0.139	0.04	0.028	9.98	0.218	6.00	0.152	0.34	0.032	99.34	0.470	0.011
MZ	1003	1002	23	54.60	0.926	0.09	0.031	28.07	0.364	0.35	0.073	0.04	0.024	10.18	0.351	5.98	0.234	0.32	0.031	99.62	0.476	0.016
MZ	988	961	24	55.15	0.506	0.11	0.018	27.88	0.526	0.38	0.062	0.04	0.017	10.28	0.323	5.85	0.214	0.35	0.034	100.03	0.483	0.016
MZ	953	930	25	55.14	0.597	0.11	0.029	28.08	0.389	0.33	0.068	0.04	0.018	10.26	0.406	5.89	0.286	0.32	0.037	100.18	0.482	0.020
MZ	921	900	24	53.62	0.872	0.10	0.032	28.44	0.657	0.39	0.135	0.05	0.050	10.94	0.719	5.44	0.372	0.24	0.048	99.22	0.519	0.036
MZ	890	875	19	54.28	0.843	0.12	0.035	27.70	0.594	0.45	0.104	0.07	0.050	10.52	0.411	5.66	0.206	0.26	0.028	99.05	0.500	0.016
LZc	847	816	20	54.44	0.373	0.11	0.029	27.65	0.409	0.42	0.102	0.09	0.095	10.54	0.345	5.51	0.184	0.29	0.088	99.06	0.505	0.017
LZc	808	798	19	54.58	0.598	0.11	0.027	28.47	0.492	0.57	0.429	0.06	0.059	10.57	0.402	5.69	0.201	0.26	0.052	100.30	0.499	0.015
LZc	784	742	20	53.95	0.542	0.10	0.030	28.55	0.459	0.46	0.254	0.06	0.061	10.85	0.395	5.60	0.212	0.30	0.097	99.89	0.508	0.017
LZc	723	703	18	53.85	0.478	0.12	0.045	28.75	0.336	0.40	0.102	0.04	0.017	11.15	0.301	5.21	0.211	0.32	0.026	99.85	0.532	0.014
LZb	703	681	20	53.21	0.827	0.10	0.021	28.72	0.310	0.44	0.099	0.04	0.014	11.01	0.337	5.45	0.182	0.28	0.034	99.24	0.519	0.015
LZb	634	580	18	53.30	0.469	0.10	0.023	28.96	0.374	0.36	0.069	0.05	0.019	11.54	0.346	5.05	0.200	0.31	0.041	99.68	0.548	0.017
LZb	558	488	29	53.01	0.837	0.11	0.019	29.03	0.414	0.44	0.116	0.06	0.057	11.56	0.550	4.96	0.336	0.31	0.054	99.45	0.553	0.028
LZb	447	367	20	52.48	0.849	0.10	0.027	29.61	0.555	0.46	0.131	0.06	0.057	11.99	0.640	4.93	0.267	0.30	0.059	99.93	0.564	0.024
LZb	346	221	18	51.88	0.526	0.10	0.034	30.03	0.375	0.41	0.096	0.05	0.025	12.52	0.332	4.66	0.219	0.26	0.038	99.91	0.589	0.017
LZb	177	173	19	51.68	0.503	0.09	0.032	30.36	0.396	0.40	0.097	0.04	0.036	12.79	0.336	4.51	0.192	0.25	0.082	100.12	0.602	0.015
LZa	161	137	17	52.41	1.098	0.10	0.024	30.13	0.731	0.37	0.050	0.04	0.027	12.40	0.835	4.77	0.435	0.27	0.083	100.49	0.581	0.040
LZa	125	96	18	51.73	0.854	0.10	0.022	30.54	0.581	0.40	0.122	0.05	0.062	12.82	0.656	4.50	0.398	0.25	0.073	100.40	0.603	0.033
LZa	96	27	18	51.81	1.564	0.08	0.029	30.01	0.968	0.31	0.070	0.03	0.024	12.66	1.061	4.50	0.638	0.26	0.052	99.66	0.599	0.054
LZa	7		6	51.42	1.162	0.10	0.013	30.58	0.716	0.33	0.026	0.06	0.017	12.72	0.916	4.48	0.534	0.21	0.101	99.90	0.604	0.047
n: number of individual mineral analyses used for each calculated average (Ave.) for three consecutive samples with 1σ SD where n > 2. Stratigraphic height is given as high and low referring to the interval used for averaging. Complete data set in Supplementary File S1. An as mole fractions.

The analyses (n = 959) record near-perfect plagioclase stoichiometry (NaAlSi₃O₈–CaAl₂Si₂O₈) with total cations of 5.024 ± 0.017 (1σ) calculated as pfu of 8 oxygens. The major cations all show strong correlation with Ca/Si = 2.982 – 0.999 Ca (∑R² = 0.983), Na+K = 0.972 – 0.894 Ca (∑R² = 0.980), and Al = 1.031 + 0.940 Ca (∑R² = 0.975). The minor element Ti (0.003) is constant, Fe (0.015) shows a systematic increase in UZ (Tegner 1997), and K (0.025) records an increase starting in MZ and continuing into UZb (Fig. 18).

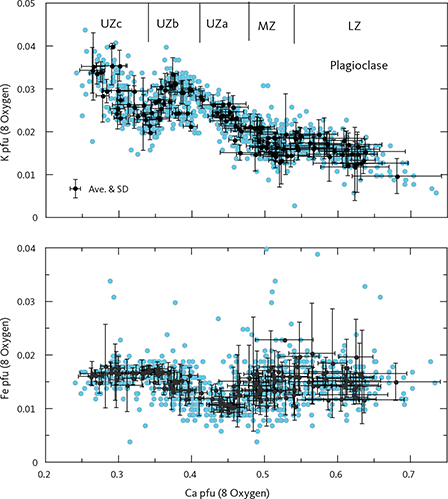
Fig. 18 Plagioclase mineral chemistry showing K and Fe as a function of Ca as cations per formula unit (pfu) normalised to 8 oxygens (Table 4). Approximate locations of the LS zone boundaries are indicated along the top of the graph. Small blue dots: analysed point compositions. Black dots: average compositions for individual thin sections with 1σ SD. Ave.: average.

Plagioclase shows dominant oscillatory and normal zoning in the HZ and LZa (Maaløe 1976a). Anorthite-rich rims (An_55–40) on normally zoned grains have, however, been reported in the LZ (Toplis et al. 2008; Humphreys 2009, 2011; Namur et al. 2014).

The results of this study can be compared to previous observations using optical methods (Wager & Deer 1939; Carr 1954; Gay & Muir 1962; Wager & Brown 1967), analyses of mineral separates (Jang & Naslund 2001) and electron microprobe analyses (Maaløe 1976a; McBirney 1989a; Tegner 1997).

4.3.3 Clinopyroxene

Average analyses of clinopyroxene are shown in Table 5. Pyroxene varies in compositions from augite to ferroaugite and ferrohedenbergite, without reaching into the salite fields in the pyroxene quadrilateral (Poldervaart & Hess 1951; Fig. 19A). The transmitted light colours of the pyroxenes are transparent to weak brownish, but transition into weak green and further to yellow and violet-brown pleochroic colours in the UZc (Wager & Deer 1939), where ferrohedenbergite coexists with inverted green ferrobustamite (Figs 10, 12). Despite extensive exsolution of low-Ca pyroxenes in the high-Ca pyroxenes, the broad electron-beam technique used in this study has largely succeeded in recording average compositions that only marginally reach into the subcalcic augite fields (Fig. 19A). The overall trend seen in the enstatite-wollastonite-ferrosalite (En-Wo-Fs) triangular diagram is similar to that reported by Brown et al. (1957) and Brown & Vincent (1963) using wet chemical and spectroscopic analyses of mineral separates and by Nwe & Copley (1975) and Nwe (1975, 1976) using electron microprobe analyses. This supports the notion that the average pyroxene compositions largely represent liquidus and subliquidus compositions. Most noticeably, the new data show the central keel in the wollastonite variation for medium Mg/(Mg + Fe^total) ratios (Fig. 19B), well established for the Skaergaard pyroxenes (Nwe 1976). This peak in the keel coincides with the disappearance of orthopyroxene, except for a couple of occurrences in the UZ.

Table 5 Average clinopyroxene compositions

Zone	Stratigraphic height (m)		n	SiO2 (wt%)		TiO2 (wt%)		Al2O3 (wt%)		FeO (wt%)		MnO (wt%)		MgO (wt%)		CaO (wt%)		Na2O (wt%)		Cr2O3 (wt%)		Total (wt%)	Mg#
	high	low		Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD		Ave.	SD
UBS	2169	2165	22	46.36	0.420	0.96	0.108	0.74	0.129	31.33	0.550	0.30	0.050	0.85	0.300	18.65	0.420	0.19	0.041	0.02	0.006	99.40	0.05	0.015
UZc	2165	2165	15	46.84	0.310	0.84	0.244	0.59	0.113	32.33	0.370	0.24	0.060	0.03	0.020	19.02	0.380	0.22	0.094	0.02	0.002	100.12	0.00	0.001
UZc	2165	2164	18	46.57	0.430	0.87	0.201	0.59	0.117	32.33	0.570	0.23	0.040	0.02	0.010	19.16	0.310	0.23	0.109	0.02	0.007	100.02	0.00	0.000
UZc	2163	2147	21	46.73	0.310	0.75	0.217	0.51	0.119	32.12	0.440	0.31	0.110	0.05	0.020	18.97	0.320	0.21	0.011	0.02	0.006	99.69	0.00	0.002
UZc	2144	2141	15	46.62	0.340	0.75	0.087	0.55	0.041	32.27	0.330	0.48	0.040	0.11	0.040	18.80	0.140	0.22	0.031	0.01	0.004	99.81	0.01	0.002
UZc	2091	2081	14	45.61	0.120	0.86	0.109	0.62	0.051	31.39	0.340	0.60	0.090	0.39	0.070	18.70	0.220	0.18	0.013	0.01		98.35	0.02	0.004
UZc	2075	2061	114	46.74	0.250	0.57	0.073	0.47	0.063	30.10	0.650	0.78	0.060	0.65	0.080	18.62	0.290	0.18	0.018	0.01	0.001	98.10	0.04	0.004
UZc	2060	2046	35	47.02	0.220	0.90	0.129	0.66	0.071	29.37	0.210	0.73	0.070	1.39	0.090	18.68	0.150	0.18	0.014	0.01		98.93	0.08	0.005
UZb	2044	2030	17	46.69	0.290	0.88	0.058	0.68	0.062	31.12	0.130	0.63	0.030	1.05	0.200	18.99	0.230	0.29	0.076	0.01	0.002	100.34	0.06	0.010
UZb	2024	1984	28	47.31	0.430	1.03	0.026	0.80	0.121	28.13	0.510	0.61	0.060	2.74	0.210	18.21	0.310	0.21	0.058			99.04	0.15	0.012
UZb	1962	1921	31	47.20	0.610	0.98	0.030	0.82	0.093	26.13	0.540	0.54	0.040	4.35	0.290	18.23	0.380	0.20	0.024	0.01		98.46	0.23	0.014
UZb	1902	1862	25	47.54	0.460	0.95	0.031	0.90	0.083	23.24	0.400	0.49	0.050	6.01	0.190	17.86	0.260	0.22	0.057			97.21	0.32	0.007
UZb	1843	1801	20	48.29	0.320	0.90	0.023	0.92	0.070	22.49	0.370	0.47	0.040	7.34	0.220	18.05	0.510	0.23	0.028	0.01	0.002	98.71	0.37	0.009
UZb	1782	1748	17	48.98	0.230	0.89	0.033	1.01	0.083	21.02	0.230	0.46	0.030	9.10	0.220	17.65	0.380	0.23	0.040			99.34	0.44	0.007
UZb	1728	1691	17	48.38	0.740	0.84	0.023	0.98	0.087	20.11	0.500	0.48	0.060	9.49	0.190	17.18	0.270	0.23	0.010			97.68	0.46	0.007
UZb	1671	1630	10	49.28	0.290	0.81	0.059	1.04	0.076	19.21	0.340	0.43	0.050	10.45	0.160	16.80	0.240	0.24	0.055			98.27	0.49	0.006
UZb	1620	1600	20	49.54	0.410	0.84	0.038	1.09	0.109	19.38	0.550	0.46	0.050	10.66	0.160	16.89	0.840	0.23	0.017	0.01		99.09	0.50	0.009
UZa	1561	1527	17	49.55	0.250	0.87	0.040	1.08	0.088	19.48	0.370	0.45	0.030	10.78	0.220	16.83	0.170	0.23	0.031			99.26	0.50	0.008
UZa	1506	1431	28	49.61	0.410	0.79	0.132	1.16	0.099	19.16	1.260	0.43	0.070	10.99	0.240	16.69	1.170	0.22	0.043	0.02	0.016	99.08	0.51	0.016
UZa	1403	1343	25	49.77	0.420	0.74	0.129	1.24	0.117	18.01	0.730	0.44	0.060	11.80	0.220	16.79	0.660	0.20	0.045	0.02	0.014	99.01	0.54	0.009
UZa	1323	1282	21	49.74	0.290	0.68	0.051	1.21	0.122	17.10	0.650	0.42	0.070	12.23	0.180	16.50	0.720	0.21	0.031	0.01	0.002	98.08	0.56	0.009
UZa	1268	1237	11	49.62	0.550	0.63	0.085	1.33	0.174	17.20	0.870	0.42	0.100	12.24	0.380	16.36	1.000	0.22	0.045			98.01	0.56	0.011
UZa	1218	1188	11	50.00	0.300	0.61	0.062	1.24	0.096	18.31	0.910	0.42	0.100	12.48	0.250	15.73	1.010	0.20	0.010	0.01		99.00	0.55	0.010
UZa	1178	1131	26	50.00	0.390	0.71	0.079	1.33	0.167	17.88	1.570	0.40	0.070	13.02	0.420	15.31	1.620	0.21	0.051	0.04	0.021	98.89	0.57	0.016
MZ	1098	1055	23	49.83	0.380	0.91	0.265	1.54	0.122	17.06	0.690	0.32	0.050	12.97	0.210	17.06	0.500	0.26	0.041	0.03	0.008	99.98	0.58	0.011
MZ	1053	1032	24	49.75	0.360	0.82	0.156	1.52	0.098	15.98	0.900	0.39	0.060	13.56	0.300	17.18	0.790	0.24	0.049	0.04	0.019	99.47	0.60	0.012
MZ	1024	1009	24	49.82	0.490	0.77	0.076	1.58	0.198	16.01	1.700	0.35	0.060	13.31	0.570	17.30	1.930	0.27	0.113	0.03	0.017	99.45	0.60	0.018
MZ	1003	1002	28	49.56	0.610	0.93	0.186	1.57	0.108	16.75	0.960	0.38	0.070	13.35	0.320	17.13	1.000	0.23	0.045	0.03	0.012	99.92	0.59	0.011
MZ	988	961	26	50.15	0.510	0.88	0.112	1.62	0.134	16.83	1.240	0.36	0.060	13.59	0.260	16.71	1.390	0.25	0.039	0.04	0.026	100.44	0.59	0.016
MZ	953	930	21	50.22	0.320	0.88	0.097	1.70	0.140	15.01	0.840	0.37	0.080	13.64	0.290	17.86	0.930	0.23	0.033	0.04	0.026	99.96	0.62	0.010
MZ	921	900	29	49.71	0.510	0.86	0.197	1.70	0.121	15.85	0.920	0.34	0.090	13.73	0.210	17.18	0.690	0.20	0.046	0.03	0.023	99.61	0.61	0.008
MZ	890	875	21	50.38	0.430	0.88	0.096	1.79	0.123	14.76	0.690	0.33	0.050	14.00	0.340	17.45	0.720	0.24	0.064	0.03	0.031	99.85	0.63	0.008
LZc	847	816	25	50.19	0.320	0.95	0.128	1.81	0.152	14.12	1.190	0.28	0.090	13.87	0.470	18.10	1.610	0.25	0.041	0.04	0.014	99.61	0.64	0.012
LZc	808	798	22	50.39	0.430	1.01	0.129	1.90	0.138	13.89	0.700	0.30	0.050	14.09	0.380	18.00	0.900	0.29	0.052	0.03	0.022	99.91	0.64	0.009
LZc	784	742	22	49.93	0.760	0.91	0.232	1.82	0.167	13.30	1.070	0.25	0.060	14.01	0.540	18.78	1.260	0.27	0.058	0.07	0.029	99.34	0.65	0.015
LZc	723	703	21	50.34	0.300	0.94	0.176	1.93	0.325	13.41	1.080	0.26	0.060	14.03	0.430	18.54	1.210	0.28	0.074	0.05	0.032	99.77	0.65	0.013
LZb	703	681	24	49.65	0.480	0.91	0.111	1.95	0.169	13.65	0.710	0.29	0.070	13.97	0.340	18.36	0.760	0.27	0.053	0.03	0.016	99.06	0.646	0.011
LZb	634	580	23	49.84	0.640	1.00	0.111	1.97	0.249	13.19	1.360	0.29	0.070	13.99	0.560	17.95	1.480	0.27	0.053	0.08	0.043	98.59	0.654	0.019
LZb	558	488	30	50.33	0.450	0.89	0.223	1.77	0.316	13.33	0.950	0.30	0.080	14.03	0.380	18.32	1.160	0.28	0.055	0.06	0.028	99.31	0.652	0.014
LZb	447	367	19	49.91	0.450	0.96	0.122	2.00	0.198	13.40	1.110	0.23	0.090	14.24	0.500	18.25	1.090	0.28	0.051	0.09	0.024	99.36	0.655	0.016
LZb	346	221	17	50.17	0.520	0.92	0.167	2.09	0.182	12.09	1.210	0.23	0.070	14.68	0.640	18.69	1.690	0.29	0.060	0.13	0.052	99.30	0.684	0.017
LZb	177	173	16	50.22	0.670	0.88	0.087	2.15	0.262	12.03	1.860	0.30	0.070	14.32	0.900	19.25	2.110	0.28	0.052	0.13	0.070	99.57	0.680	0.026
LZa	161	137	16	50.70	0.270	0.81	0.152	2.19	0.235	11.04	1.150	0.27	0.070	14.75	0.710	19.20	1.490	0.31	0.057	0.09	0.081	99.36	0.704	0.018
LZa	125	96	17	50.35	0.520	0.83	0.158	2.13	0.189	10.75	0.630	0.24	0.070	14.66	0.650	19.76	1.330	0.35	0.069	0.06	0.057	99.15	0.709	0.007
LZa	96	27	18	50.21	0.870	0.88	0.270	2.08	0.282	10.95	1.830	0.27	0.060	15.09	0.970	19.19	2.060	0.30	0.070	0.07	0.041	99.02	0.710	0.026
LZa	7		4	50.14	0.230	0.87	0.083	2.09	0.201	11.08	2.130	0.19	0.080	15.67	0.380	18.17	1.580	0.26	0.056	0.16	0.126	98.63	0.716	0.042
n: number of individual mineral analyses used for each calculated average (Ave.) for three consecutive samples with 1σ SD where n > 2. Stratigraphic height is given as high and low referring to the interval used for averaging. Complete data set in Supplementary File S1.

The variation in the clinopyroxene compositions parallels that for olivine with initial weak upward decrease in En content (LZa En_54.0–En_38.1; LZa En_48.3–En_36.3; LZc En_44.3–En_36.9) and a subsequent stronger decrease from the upper MZ and into the UZ (MZ En_45.5–En_35.1; UZa En_41.3–En_29.4; UZb En_32.6–En_5.8; UZc En_6.6–En_0.0). The drop in wollastonite amounts to about 15 wt% from Wo₃₉ in LZa to Wo₃₃ in MZ (Fig. 19B). Augite in the HZ reaches a maximum of En_41.5 (Wo_45.0En_41.5Fs_13.5) at about 50 m before the base of the Cambridge Drill Core (Nwe 1976).

The total amount of cations in clinopyroxenes calculated for 6 oxygens (n = 1060) is 4.023 ± 0.014 (1σ), only slightly over the ideal stoichiometry of 4 cations. The negative correlation between total Fe and Mg is offset from the ideal 1:1 ratio (Fe = 1.123 – 0.829 Mg (∑R² = 0.943)) and does not improve if Mn is added to Fe (Fe + Mn = 1.141 – 0.838 Mg (∑R² = 0.942)). This offset is attributed to ferric iron that is calculated as part of the total iron content and may increase with increasing total Fe.

Details of the compositional variation are shown in Figs 20 and 21, here normalised to 4 cations and 6 oxygens. Aluminium shows a marked decrease as a function of Mg from 0.11 pfu throughout the LZ and MZ and thereafter levels at about 0.05 in UZa, forming a sloping plateau until the middle of UZc when it reaches c. 0.04, and followed by a slight decrease to c. 0.03 pfu for the ferrohedenbergites of the SH (Fig. 20). Titanium is much lower than Al, showing a decrease from c. 0.03 pfu through the LZ to 0.02 pfu in MZ. In contrast to Al, Ti forms a slightly increasing plateau from 0.02 to 0.03 pfu, and ends with a terminal decrease from the middle of UZc to c. 0.02 at the SH. Aluminium occurs dominantly as tetrahedral Al^iv with little octahedral Al^vi and mostly in the UZ (not shown). Of the analysed clinopyroxenes, only 18% can be calculated to contain octahedral Al at an average 0.015 pfu, about a quarter of the average 0.06 pfu content of tetrahedral Al.

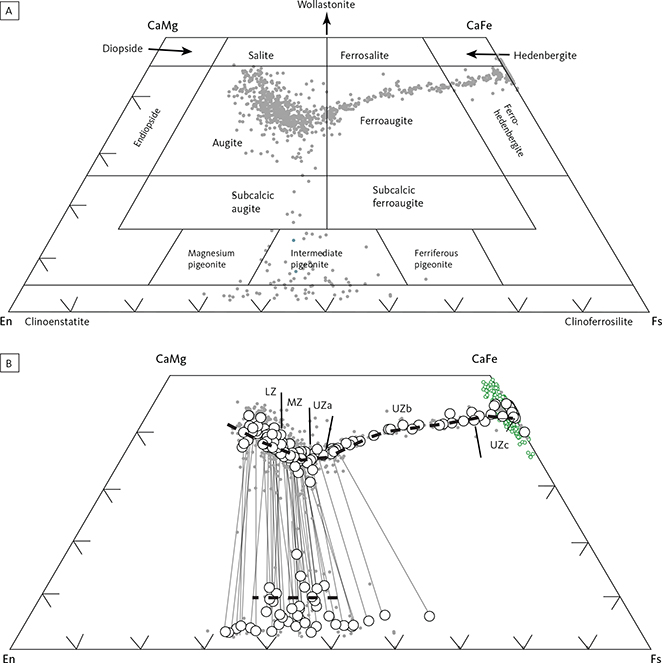
Fig. 19 The pyroxene quadrilateral diagram for the Skaergaard pyroxenes on a molecular basis. A: nomenclature of Poldervaart & Hess (1951) with the cloud of analyses from this study. B: details of analysed pyroxenes (Table 5). Small solid grey dots: individual analyses. Small open green circles: inverted ferrobustamite of the UZc. Large open circles: average analyses for individual sections. Thin grey lines: tie-lines between coexisting average high-Ca and low-Ca pyroxenes. Iron was calculated as total Fe. Black dashed lines: solidus trends for the Skaergaard intrusion established by Nwe (1976). En: enstatite. Fs: ferrosilite. CaMg: diopside. CaFe: hedenbergite. Approximate locations of the Skaergaard zone boundaries are indicated along the high-Ca pyroxene solidus trend. Abbreviations for LS divisions in Fig. 2.

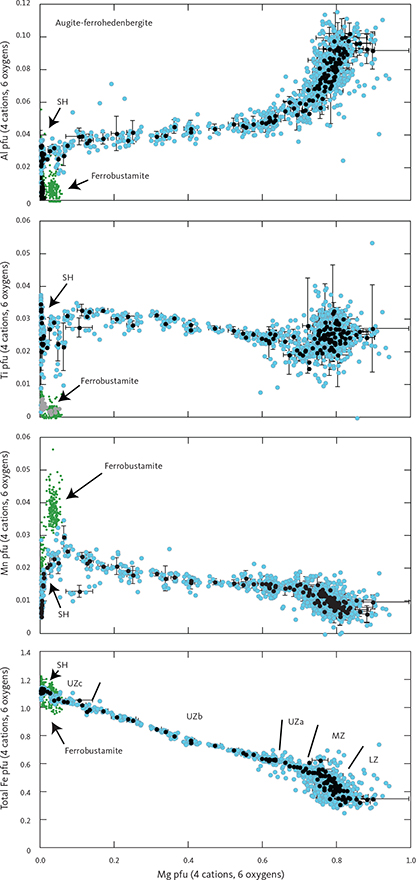
Fig. 20 Variation diagrams as a function of Mg content for selected cations of augite-ferrohedenbergite pyroxenes calculated per formula unit (pfu) of 4 cations and 6 oxygens. Iron has been partitioned between Fe²⁺ and Fe³⁺ using charge balance (Papike et al. 1974). Blue dots: total database of high-Ca pyroxenes. Small green dots: inverted ferrobustamite (or green ferrohedenbergite) of UZc. Black dots: average composition for individual thin sections with 1σ SD. Approximate locations of the LS zone boundaries are shown in the total Fe (bottom) panel. SH (Sandwich Horizon) refers to the brown ferrohedenbergite of the UZc. Abbreviations for LS divisions in Fig. 2.

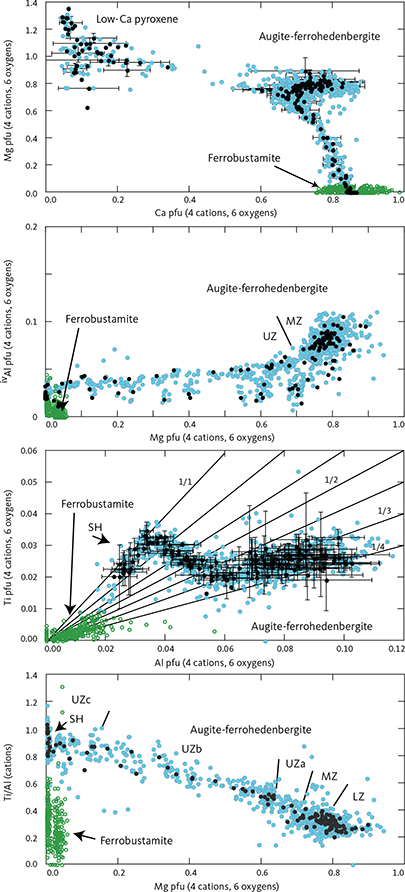
Fig. 21 Variation diagrams as a function of Mg, Ca, and Al content for elected cations and ratios of augite-ferrohedenbergite pyroxene calculated per formula unit (pfu) of 4 cations and 6 oxygens. Iron has been partitioned between Fe²⁺ and Fe³⁺ using charge balance (Papike et al. 1974). Symbols and notations in Fig. 20. Mg vs. Ca (top panel) shows both clino- and orthopyroxenes (cf. Fig. 19).

The Ti/Al ratio increases markedly with decreasing Mg (Ti/Al = 0.929 + 0.761 Mg (∑R² = 0.844)). This translates into a systematic variation as a function of decreasing Al from a Ti/Al of 0.25 in the LZa to 0.40 through the LZ to MZ, followed by a sharp transgression to 1.0 through the UZ and capped by a constant ratio in the SH (Fig. 21; Nwe & Copley 1975).

Manganese shows a systematic increase from 0.01 pfu with a deflection in UZa until reaching 0.25 at the base of UZc, followed by a marked decrease to c. 0.01–0.02 pfu in the terminal brown ferrohedenbergites of the SH where it coexists with Mn-rich inverted ferrobustamite (Fig. 20). Sodium is present at about 0.018 ± 0.005 pfu (1σ) through the LS, slightly decreasing past the middle of UZb (not shown). Chromium is below the detection limits for the UZ but may reach 0.005 pfu in the LZ.

Ferric iron content, estimated by charge-balancing non-quadrilateral elements (Al^vi+2Ti+Cr versus Na+Al^iv; Papike et al. 1974) is shown in Fig. 22. Because of the low content of Na, Cr and Al^vi in most Skaergaard pyroxenes, this is basically a balance of 2Ti against Al^iv. Although such estimates do not often correlate well with directly measured values, the results suggest that the Fe³⁺ content of Skaergaard pyroxenes is largely constant throughout the LZ and MZ (0.06–0.04 pfu) and thereafter form a broad up-section increasing plateau towards a small negative content of Fe³⁺ in UZc. The estimated Fe³⁺ shows an initial marked drop in the LZ and MZ with a subsequently low-sloping trend towards slightly negative values (Fig. 22).

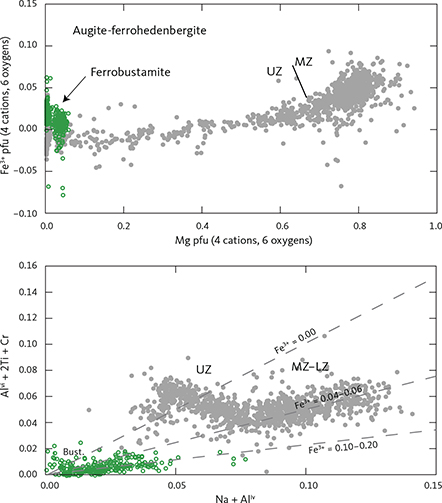
Fig. 22 Ferric iron estimate for the high-Ca pyroxenes using the charge balance equation Fe³⁺ = Al^iv + Na – Al^vi – Cr – 2Ti of Papike et al. (1974). The Fe³⁺ content decreases systematically from 0.10–0.20 pfu in the UZc green inverted ferrobustamite (Bust.), to 0.04–0.06 in the LZ and MZ augite, and decreases further in UZ augite-ferrohedenbergite to reach negative charge balance values.

If Fe³⁺ is estimated by bulk charge balance, the Fe³⁺ content is not markedly different from the non-quadrilateral charge balance, except that the absolute values are somewhat higher (0.05 ± 0.03 pfu, 1σ), with no systematic variation with Mg content and no negative values. Because of the constancy in Fe³⁺, the Fe³⁺/Fe²⁺ ratio shows a variation with Mg content that mimics the Fe³⁺ variation seen in Fig. 22 and calculated by the method of Papike et al. (1974). If Fe³⁺ cations were expressed as a ratio of the total iron, Fe³⁺/(Fe²⁺+Fe³⁺), the results would be relatively constant for the two segments of Fig. 22: 0.07 ± 0.04 (1σ) for the UZ and 0.28 ± 0.14 for the MZ and LZ. The latter, however, decreases slightly upward. Although caution is warranted using charge-balance calculations, the results suggest that Fe³⁺ (and the Fe³⁺/Fe²⁺ ratio) decreases through the LZ and MZ and reaches constant low values, approaching zero Fe³⁺, in the UZ. It is, however, possible that the high Ti/Al ratio correlated with low calculated Fe³⁺ may signal the presence of reduced Ti³⁺ as suggested for some Lunar pyroxenes (Bence & Papike 1972).

Cation occupancy suggests that the structural tetrahedral site in pyroxene (T-site) is predominantly filled by Si and Al^iv and that the amount of Fe³⁺ occupying octahedral sites (i.e. structural octahedral sites in pyroxene; M-sites) markedly decreases in the LZ and MZ to low or zero in UZ. Aluminium occurs predominantly in tetrahedral (Al^iv) coordination with lesser amounts in octahedral coordination (Al^vi). The average deficiency in total T-site occupancy (Si+Al^vi) to an ideal value of 2.00 is 0.02 that may be due to Fe³⁺ or other tetrahedral cations that were not analysed.

The total of the non-quadrilateral components, calculated according to Cawthorn & Collerson (1974) and using bulk charge-balance Fe^3––Fe²⁺ partitioning, amounts to 11–5% that correlates positively with Mg. The only non-quadrilateral components are c. 3.5–1% Ca-Ti-tschermakite (CaTiAl₂O₆), c. 4–0% Ca-Fe³⁺-tschermakite (CaFe³⁺AlSiO₆), 2–0% Ca-tschermakite (CaAl₂SiO₆) and 3–1.5% jadeite (NaAlSi₂O₆). The calculated molecules indicate a final propagated error of silica excess amounting to 0.03 ± 0.03 pfu (1σ).

Most calculated and total non-quadrilateral molecules show a systematic decrease throughout the LZ to UZa and are replaced by a constant or slight increase throughout UZb to UZc – all as a positive function of decreasing Mg (Fig. 23). Jadeite decreases through the LZ to UZa and is constant at about 1.5% throughout UZb to UZc. The Ca-Ti-tschermakite varies in the LZ to UZa, and mirrors jadeite, but shows a systematic increase in UZb, followed by a drop in UZc. The calculated Ca-ferri-tschermakite molecule is dependent on the Fe³⁺–Fe²⁺ partitioning model chosen. The model used here results in a systematic decrease throughout the LZ to UZa and extending into the lower part of the UZb, after which Fe³⁺ can no longer be calculated. Finally, Ca-tschermakite likewise decreases throughout the LZ to UZa after which octahedral Al can no longer be assigned. These variations mimic the overall elemental variations in pyroxenes by showing a noticeable break in compositional variation between the LZ to UZa and UZb to UZc. Most noticeable is the suggestion that Fe³⁺ occurs in tetrahedral coordination and that octahedral Al is not suggested to be present in UZb to UZc.

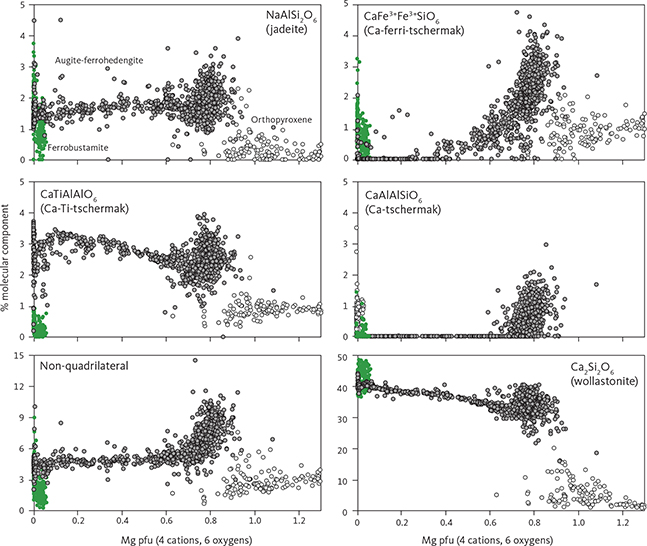
Fig. 23 Percentage of the main modelled non-quadrilateral molecular components of the pyroxene solid solution as a function of Mg pfu. Shown are both the high-Ca (solid grey circles) and the low-Ca pyroxenes (open circles). See Section 4.3.3 for a discussion of the choice of molecular components. The non-quadrilateral component is the total of all components, excluding wollastonite, enstatite and ferrosilite. Ferrobustamite is the green ferrohedenbergite believed to have inverted from ferrobustamite (small green circles). The only quadrilateral component shown is wollastonite.

General cation substitutions for terrestrial augites are dominated by single exchange components (Fe²⁺,Mn)(Mg)_–1, Ca(Mg)_–1, Fe³⁺(Al)_–1, and the coupled exchange components TiAl₂(MgSi₂)_–1, Fe³⁺Al(MgSi)_–1 and NaAl(2Mg)_–1 (Cawthorn & Collerson 1974; Robinson 1980; Papike 1980; Basaltic Volcanism Study Project 1981; Sack & Ghiorso 1994). In some respects, these substitutions differ from the observed uppermost UZ pyroxenes. The differences stem from the generally low Si content of hedenbergite, requiring most Al to be allocated to the tetrahedral site and largely prohibiting octahedral Al as well as octahedral Fe³⁺. The Pearson matrices of Table 6 show that the dominating non-quadrilateral correlations in the overall intrusion are Al^iv–Fe³⁺ and Ti–Al^iv. The main difference is between the two stratigraphic parts, such that in the upper part (UZb to UZc) the quadrilateral correlation (Mg,Fe²⁺)–Ca becomes important.

Table 6 Pearson product moment correlation coefficient (r) matrices for non–quadrilateral and quadrilateral cations in clinopyrozene

Subzones UZc–UZb
	Ti	Alvi	Aliv	Fe3+	Fe2+	Mn	Mg	Ca	Na
Ti	1.00
Alvi	–0.17	1.00
Aliv	0.39	–0.46	1.00
Fe3+	–0.23	–0.51	0.91	1.00
Fe2+	0.10	–0.39	–0.45	–0.23	1.00
Mn	–0.01	0.06	–0.05	–0.07	–0.03	1.00
Mg	–0.11	0.37	0.47	0.25	–1	–0.01	1.00
Ca	0.15	–0.48	–0.34	–0.16	0.92	–0.02	–0.94	1.00
Na	–0.11	–0.02	0.08	0.46	–0.14	–0.06	0.13	–0.16	1.00
Zones LZ–UZa
	Ti	Alvi	Aliv	Fe3+	Fe2+	Mn	Mg	Ca	Na
Ti	1.00
Alvi	–0.23	1.00
Aliv	0.40	–0.6	1.00
Fe3+	–0.04	–0.7	0.87	1.00
Fe2+	–0.13	0.29	–0.83	–0.76	1.00
Mn	–0.19	0.26	–0.64	–0.54	0.72	1.00
Mg	0.15	–0.32	0.69	0.60	–0.7	–0.55	1.00
Ca	0.09	–0.2	0.51	0.49	–0.72	–0.52	0.05	1.00
Na	0.23	–0.09	0.44	0.45	–0.49	–0.31	0.22	0.38	1.00

In summary, the dominating pattern of cation variation is a negative correlation between Fe²⁺ and Mg with a positive correlation between Fe²⁺ and Ca, becoming noticeable in the UZ. The tetrahedral site is occupied by Si and Al^iv, while Fe³⁺ occurs in octahedral sites together with a small amount of Al^vi. The Fe³⁺ calculated by charge balancing decreases in the LZ and MZ and reaches low concentrations in UZ. Although the absolute variation of Ti decreases upward in the stratigraphy, the Ti/Al ratios show an overall increase upward in the stratigraphy, controlled by corresponding decreasing Al.

The observation that Al largely occupies tetrahedral sites in the Skaergaard clinopyroxenes concurs with previous work (Muir 1951; Brown et al. 1957; Brown & Vincent 1963; Nwe 1975, 1976; Nwe & Copley 1975). Direct measurements of the ferric iron content of the Skaergaard augite to hedenbergite series by Brown et al. (1957) and Brown & Vincent (1963) indicate a marked decrease in the average Fe³⁺/Fe²⁺ ratio from the LZ and MZ (0.120) into the UZ (0.049), thus supporting our observation of Fe³⁺ content in the UZ pyroxenes.

4.3.4 Ferrobustamite

Under the general heading of ‘ferrobustamite’ is described the fine mosaic of green hedenbergite that characterises the pyroxenes of the UZc and is believed to have inverted from a triclinic ferrobustamite (Naslund 1984). Bustamite is a triclinic pyroxenoid, (Mn,Ca,Fe)₂Si₂O₆, that is similar to wollastonite with Fe and Mn substituting for Ca (1.5% Mn, 55.3% Fe²⁺ and 43.2% Ca). Thus, the Skaergaard ferrobustamite was traditionally referred to as ferrowollastonite with Fe substituting for Ca to approximately equal amounts (Wager & Deer 1939; Brown & Vincent 1963; Lindsley et al. 1969; Nwe & Copley 1975). However, in many respects, the Skaergaard inverted bustamite differs from classic occurrences of bustamite in metasomatised skarn deposits by their higher Fe²⁺ and lower Mn (Mason 1975; Deer et al. 1978). Bustamite inverts to a fine-grained mixture of wollastonite and ferrohedenbergite or to pure ferrohedenbergite (Brown & Guy 1960) during cooling around 950°C for compositions and conditions relevant to the UZc of the Skaergaard intrusion (Lindsley et al. 1969; Rutstein 1971; Rutstein & White 1971; Deer et al. 1978).

The green ferrohedenbergite is easily identified not only petrographically (Fig. 10), but also compositionally, by low Ti and high Mn compared to the coexisting brown ferrohedenbergite (Fig. 12; Table 7). The mosaic grains of the green ferrohedenbergite are first detected intermittently just below the UZc at 2051 m in the stratigraphy, become abundant in UZc and persist into the SH. The green ferrohedenbergite shows little or no compositional variation as a function of Mg content or stratigraphic position. The Fe²⁺ content is constant at 1.084 ± 0.048 and Fe³⁺ at 0.014 ± 0.011 pfu (n = 289), suggesting a small, but generally persistent, ferric iron content in contrast to the coexisting brown ferrohedenbergite (Fig. 22), where the presence of Fe³⁺ is not detected by charge-balance calculations.

Table 7 Average ferrobustamite compositions per sample

Zone	Sample ID	Stratigraphic height	n	SiO2 (wt%)		TiO2 (wt%)		Al2O3 (wt%)		FeO (wt%)		MnO (wt%)		MgO (wt%)		CaO (wt%)		Na2O (wt%)		Cr2O3 (wt%)		Total (wt%)	Mg#
		(m)		Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD		Ave.	SD
UBS	458634	2168	13	47.39	0.127	0.12	0.034	0.26	0.121	31.24	1.097	0.37	0.120	0.09	0.037	19.99	1.075	0.21	0.072	0.02	0.008	99.63	0.000	0.003
UZc	458636	2165	9	47.37	0.123	0.12	0.045	0.33	0.076	31.67	1.141	0.48	0.093	0.05	0.033	19.67	0.986	0.27	0.055	0.01	0.006	99.96	0.003	0.002
UZc	458637	2165	4	46.61	0.462	0.10	0.040	0.23	0.105	32.30	1.904	0.39	0.076	0.01	0.003	19.80	1.321	0.35	0.134	0.02	0.005	99.79	0.000	0.001
UZc	458638	2165	9	47.53	0.153	0.13	0.018	0.28	0.110	31.83	1.245	0.34	0.030	0.04	0.012	19.60	1.217	0.18	0.043	0.02	0.000	99.95	0.002	0.001
UZc	458639	2165	8	47.59	0.623	0.14	0.066	0.26	0.107	31.52	1.244	0.37	0.054	0.05	0.023	19.70	1.173	0.14	0.036	0.02	0.002	99.81	0.003	0.002
UZc	458640	2164	4	46.92	0.373	0.18	0.047	0.28	0.066	32.83	0.986	0.40	0.021	0.03	0.011	18.78	0.387	0.42	0.399	0.01	0.000	99.85	0.002	0.001
UZc	458641	2164	5	47.70	0.135	0.11	0.055	0.22	0.087	31.10	0.666	0.44	0.124	0.08	0.037	20.10	0.692	0.15	0.028	0.02	0.008	99.92	0.005	0.003
UZc	458642	2162	1	46.86		0.09		0.38		34.05		0.46		0.01		17.36		0.27		0.02		99.51	0.001
UZc	458643	2150	9	47.70	0.366	0.17	0.093	0.21	0.109	31.41	0.865	0.51	0.061	0.06	0.035	19.93	0.805	0.23	0.040	0.01	0.005	100.22	0.003	0.002
UZc	458644	2147	7	47.50	0.235	0.19	0.090	0.26	0.104	31.79	1.538	0.64	0.171	0.08	0.062	19.15	1.302	0.14	0.032	0.01	0.003	99.77	0.005	0.004
UZc	458645	2144	9	46.96	0.199	0.14	0.051	0.35	0.180	32.43	1.348	0.84	0.088	0.09	0.069	18.25	0.942	0.24	0.084	0.01	0.001	99.31	0.005	0.004
UZc	458646	2144	9	47.90	0.263	0.08	0.081	0.16	0.102	30.05	0.704	0.73	0.084	0.11	0.072	20.40	0.800	0.24	0.054	0.01	0.000	99.69	0.006	0.004
UZc	458647	2141	1	46.39	0.263	0.14	0.000	0.85	0.000	32.60	0.000	0.57	0.000	0.16	0.000	18.73	0.000	0.38	0.000			99.81	0.009
UZc	0.7	2091	116	47.14	0.613	0.07	0.035	0.21	0.126	32.63	0.899	1.10	0.117	0.44	0.080	18.21	0.568	0.10	0.039	0.02	0.010	99.92	0.023	0.004
UZc	458652	2089	?	46.69	0.369	0.06	0.072	0.12	0.096	29.59	1.026	1.06	0.132	0.36	0.064	20.53	0.666	0.08	0.039	0.02	0.005	98.34	0.021	0.003
UZc	458653	2075	9	46.86	0.162	0.04	0.016	0.15	0.041	28.96	1.015	1.15	0.123	0.45	0.112	20.28	0.574	0.08	0.013	0.01	0.006	97.99	0.027	0.007
UZc	20.8	2071	102	46.73	0.533	0.05	0.035	0.08	0.086	30.39	0.616	1.04	0.101	0.61	0.092	18.15	0.763	0.11	0.047	0.01	0.000	97.18	0.035	0.005
UZc	31.1	2061	9	46.29	0.561	0.09	0.045	0.16	0.223	30.04	0.976	1.10	0.116	0.61	0.045	17.88	0.975	0.13	0.073			96.30	0.035	0.002
UZc	458658	2060	1	46.57	0.561	0.11	0.000	0.19	0.000	34.65	0.000	0.74	0.000	0.23	0.025	17.05	0.000	0.32	0.000			99.85	0.012
UZc	40.9	2051	12	47.63	0.507	0.09	0.075	0.12	0.149	28.70	1.046	1.25	0.150	0.80	0.087	19.73	0.791	0.08	0.040			98.39	0.047	0.005
n: number of individual mineral analyses used for each calculated average (Ave.) for three consecutive samples with 1σ SD where n > 2.

The Mg content of the green ferrohedenbergite is 0.021 ± 0.017, Mn 0.030 ± 0.011, Al 0.009 ± 0.002, Ti 0.003 ± 0.002 and Na 0.012 ± 0.007 pfu identifying hedenbergite inverted from bustamite by low Ti (and Al and Ti/Al) and relatively high Mn compared to the coexisting brown ferrohedenbergite (Figs 20, 21). The corresponding concentrations for the coexisting brown ferrohedenbergite (n = 123) are Mn 0.014 ± 0.006, Al 0.030 ± 0.007, Ti 0.027 ± 0.007 and Na 0.016 ± 0.006 pfu. The Mn/Fe²⁺ ratio for the green ferrohedenbergite (0.028 ± 0.011) is double that for the coexisting brown ferrohedenbergite (0.013 ± 0.006 pfu), further supporting the contention that the former is a polymorph of Mn-enriched ferrobustamite (Mason 1975). Another significant feature of the green ferrohedenbergite is that the tetrahedral sites (Si+Al+Fe³⁺) are filled (T-sites = 2.000 ± 0.014 pfu), leaving some Al and Fe³⁺ in octahedral site positions. The result is that they show low non-quadrilateral components with low Ca-Ti-tschermakite and high Ca-ferri-tschermakite when compared to the coexisting brown ferrohedenbergites.

4.3.5 Orthopyroxene

Orthopyroxene appears throughout the LZ, MZ and into UZa in variable amounts and compositions within the intermediate (inverted) pigeonite and enstatite-ferrosilite fields of Poldervaart & Hess (1951; Fig. 19A). The analyses (n = 127) suggest subsolidus equilibration from clinopyroxene (including pigeonite) for a subset of the analyses by exsolution and grain-coarsening resulting in a decrease in the wollastonite content to a low of 2% into the enstatite-ferrosilite field. On the other hand, a subset of analyses is consistent with the overall variation (Table 8) expected for inverted pigeonite with a wollastonite content of c. 10% and similar to values reported by Brown et al. (1957) using wet chemical analyses of mineral separations and Nwe (1976) using electron microprobe analyses.

Table 8 Average orthopyroxene compositions

Zone	Stratigraphic height (m)		n	SiO2 (wt%)		TiO2 (wt%)		Al2O3 (wt%)		FeO (wt%)		MnO (wt%)		MgO (wt%)		CaO (wt%)		Na2O (wt%)		Cr2O3 (wt%)		Total (wt%)	Mg#
	high	low		Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD		Ave.	SD
UZb	1671	1630	4	49.37	0.082	0.21	0.103	0.30	0.157	33.09	2.189	0.67	0.050	12.92	0.064	2.77	1.974	0.04	0.019	0.00	0.000	99.37	0.410	0.016
UZb	1620	1600	1	49.86		0.22		0.39		37.37		0.76		10.64		2.67		0.06		0.00		101.96	0.337
UZa	1561	1527
UZa	1506	1431
UZa	1403	1343	1	49.79		0.15		0.41		32.60		0.67		14.25		2.31		0.02		0.00		100.19	0.438
UZa	1323	1282	4	51.23	0.105	0.20	0.051	0.48	0.090	31.68	0.725	0.65	0.058	15.48	0.385	1.84	0.660	0.08	0.107	0.01	0.001	101.64	0.465	0.009
UZa	1268	1237	2	50.91		0.34		0.58		28.63		0.64		16.24		2.74		0.03		0.01		100.13	0.503
UZa	1218	1188	3	50.64	0.295	0.13	0.024	0.62	0.035	30.69	0.808	0.67	0.059	15.81	0.683	1.93	0.792	0.02	0.007	0.00	0.000	100.52	0.479	0.014
UZa	1178	1131	5	50.41	0.235	0.25	0.022	0.51	0.076	30.81	1.243	0.63	0.082	15.78	0.454	2.00	0.467	0.02	0.016	0.00	0.000	100.40	0.477	0.016
MZ	1098	1055	6	50.82	0.249	0.29	0.079	0.65	0.073	27.26	1.395	0.50	0.120	16.42	0.919	4.59	1.592	0.04	0.037	0.03	0.000	100.58	0.518	0.015
MZ	1053	1032	6	50.29	0.695	0.28	0.116	0.73	0.167	26.19	2.113	0.57	0.106	17.88	1.068	3.50	1.890	0.10	0.119	0.01	0.014	99.55	0.549	0.022
MZ	1024	1009	8	50.11	1.148	0.44	0.669	0.78	0.088	26.14	0.880	0.53	0.128	17.19	0.912	4.59	1.582	0.09	0.123	0.01	0.000	99.87	0.541	0.011
MZ	1003	1002	4	49.75	0.879	0.43	0.285	0.79	0.142	26.84	2.654	0.49	0.103	16.84	0.504	4.96	2.437	0.06	0.043	0.01	0.000	100.18	0.528	0.019
MZ	988	961	6	50.97	0.192	0.29	0.038	0.73	0.074	26.39	1.250	0.50	0.068	18.02	0.278	3.82	1.036	0.03	0.038	0.02	0.011	100.77	0.549	0.012
MZ	953	930	6	51.10	0.545	0.33	0.041	0.67	0.098	26.71	0.393	0.52	0.106	18.32	0.896	2.85	1.510	0.03	0.020	0.05	0.018	100.59	0.550	0.010
MZ	921	900	1	51.20		0.36		0.55		26.22		0.50		18.20		3.75		0.08		0.02		100.88	0.553
MZ	890	875
LZc	847	816	1	51.23		0.35		2.04		22.82		0.40		19.05		4.08		0.00		0.03		99.99	0.598
LZc	808	798	1	50.96		0.38		0.72		25.37		0.48		20.00		2.08		0.00		0.00		100.00	0.584
LZc	784	742	3	51.21	0.574	0.33	0.029	0.83	0.127	23.38	0.721	0.40	0.110	20.30	0.606	3.27	1.597	0.08	0.042	0.07	0.016	99.87	0.607	0.006
LZc	723	703	2	52.16		0.35		0.64		25.56		0.56		19.79		2.78		0.06		0.00		101.88	0.580
LZb	703	681	1	50.66		0.34		0.78		25.12		0.48		18.99		3.93		0.03		0.00		100.33	0.574
LZb	634	580
LZb	558	488	2	51.63		0.39		0.85		22.80		0.48		20.65		3.08		0.06		0.02		99.96	0.617
LZb	447	367	2	51.16		0.35		1.00		25.36		0.39		19.71		2.46		0.05		0.05		100.53	0.580
LZb	346	221	1	51.25		0.36		0.87		21.78		0.42		20.81		3.31		0.05		0.02		98.86	0.629
LZb	177	173	5	51.41	0.284	0.29	0.030	0.95	0.188	24.01	1.610	0.48	0.105	20.91	1.122	1.94	1.823	0.02	0.015	0.02	0.017	100.03	0.608	0.023
LZa	161	137	4	52.47	0.691	0.31	0.029	0.84	0.055	21.57	0.345	0.41	0.095	22.35	0.675	1.85	0.663	0.01	0.034	0.03	0.044	99.83	0.649	0.009
LZa	125	96	5	52.22	0.385	0.33	0.061	0.90	0.089	20.13	0.672	0.35	0.042	23.51	0.693	1.36	0.172	0.03	0.024	0.04	0.019	98.87	0.587	0.013
LZa	96	27	2	52.08		0.31		0.97		19.56		0.37		23.82		1.31		0.03		0.06		98.51	0.68
LZa	7		2	51.82		0.31		0.92		22.30		0.40		22.66		1.12		0.01		0.01		99.54	0.644
n: number of individual mineral analyses used for each calculated average (Ave.) for three consecutive samples with 1σ SD where n > 2. Stratigraphic height is given as high and low referring to the interval used for averaging. Complete data set in Supplementary File S1.

Like the augite-ferrohedenbergites, the low-Ca pyroxenes have tetrahedral sites that are mostly filled by Al and Fe³⁺ (T-sites = 1.989 ± 0.024 pfu) with total Fe³⁺ estimated by charge balance as 0.075 ± 0.004 pfu. The minor elements Ti, Al and Na are all below c. 0.05 pfu giving a total non-quadrilateral component of 2.7% ± 1.0% made-up of jadeite (0.36% ± 0.42%), Ca-ferri-tschermakite (0.87% ± 0.42%), Ca-Ti -tschermakite (0.90% ± 0.47%) and Ca-tschermakite (0.60% ± 0.48%; Fig. 23). The propagated error of silica excess is 0.041 ± 0.039 pfu (1σ).

4.3.6 FeTi oxides

FeTi oxides appear throughout the LS, although first in LZc in appreciable amounts as ilmenite and magnetite primocrysts. The highest amounts of both phases are found in the centre of LZc (Fig. 15). Ilmenite is often homogeneous without exsolution or oxidation lamella of hematite. Magnetite on the other hand is composed mostly of an intergrowth of magnetite and ilmenite, resulting from exsolution of ulvöspinel lamella and subsequent oxidation to secondary ilmenite (Vincent 1960). Ilmenite compositions are calculated based on a formula unit of 2 cations and 3 oxygens, while magnetite is calculated based on 3 cations and 4 oxygens. Iron is partitioned between Fe²⁺ and Fe³⁺ based on charge balance. The solid-solution components are calculated as hematite and ilmenite for ilmenite and ulvöspinel and magnetite for magnetite. Representative coexisting magnetite and ilmenite are shown in Table 9. Ilmenite (n = 405) contains an average of 8% hematite (Fig. 24A) and appreciable amounts of Mn (0.012 ± 0.006 pfu) and Mg (0.054 ± 0.039 pfu). Magnetite (n = 248) generally appears in small amounts throughout the LS together with ilmenite. The magnetite content in the solid solution varies considerably reaching much higher values (Fig. 24A) than those found experimentally on Skaergaard-like melts (Thy et al. 2008); presumably reflecting exsolution and re-equilibration in the natural material (Vincent & Phillips 1954; Vincent 1960; Buddington & Lindsley 1964). Of the minor elements, only Al (0.118 ± 0.057 pfu) and Mg (0.029 ± 0.023 pfu) occur in appreciable amounts in the magnetite solid solution (Table 9). Vanadium occurs in both ilmenite (V₂O₃ < 0.3%) and magnetite (V₂O₃ < 1.7%; Vincent & Phillips 1954; Jang & Naslund 2003; Jang et al. 2001) but was not analysed during this study. The T (°C) and oxygen fugacity normalised to the nickel-nickel oxide (NNO) oxygen buffer and expressed as ∆logfO₂ (NNO) for the coexisting magnetite and ilmenite pairs were estimated using the geothermometry-oxybarometry technique of Ghiorso & Evans (2008) and shown in Table 9.

Table 9 Representative coexisting magnetite and ilmenite compositions per sample

Magnetite
Zone	Sample ID	Stratigraphic height	n	SiO2 (wt%)		TiO2 (wt%)		Al2O3 (wt%)		FeO* (wt%)		MnO (wt%)		MgO (wt%)		CaO (wt%)		Cr2O3 (wt%)		NiO (wt%)		FeO (wt%)	Fe2O3 (wt%)	Total (wt%)	XUlv	XMt	T (°C)	∆logfO2 (NNO)
		(m)		Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD
UZc	458636	2165	3	0.23	0.123	15.68	2.682	0.56	0.102	79.96	1.929	0.34	0.097	0.01	0.000	0.02	0.02	0.03	0.006	0.05	0.019	45.79	37.97	100.66	0.461	0.539	682	–1.58
UZc	458637	2164	1	1.72		4.36		0.49		88.64		0.12		0.01		0.01		0.01		0.03		37.62	56.69	101.05	0.136	0.864	502	0.03
UZc	458638	2163	1	0.11		17.40		0.94		77.73		0.10										47.33	33.78	99.66	0.528	0.472	739	–1.26
UZc	458639	2162	2	0.13		14.21		0.60		80.29		0.18		0.04		0.06				0.03		44.03	40.28	99.55	0.423	0.577	678	–3.28
UZc	458640	2160	2	0.07		13.45		0.56		81.78		0.12						0.01		0.02		43.67	42.34	100.24	0.397	0.603	620	–3.27
UZc	458642	2155	2	0.08		17.13		0.41		78.14		0.17		0.01		0.03						46.76	34.88	99.47	0.503	0.497	726	–1.34
UZc	458643	2150	4	0.16	0.137	16.70	2.329	0.45	0.103	80.12	2.251	0.29	0.082	0.02	0.000	0.03	0.020	0.01	0.004	0.01	0.000	46.93	36.87	101.48	0.483	0.517	773	–0.76
UZc	458644	2147	2	0.75		5.30		0.39		88.61		0.15		0.01		0.02						37.14	57.19	100.94	0.158	0.842	499	–0.57
UZc	458645	2144	2	2.21		5.04		0.48		87.64		0.09		0.03		0.03				0.06		38.85	54.21	101.00	0.160	0.840	466	–1.09
UZc	458646	2144	2	0.58		18.63		0.16		76.41		0.79		0.02		0.04		0.02		0.03		48.20	31.34	99.79	0.542	0.458	816	–0.80
UZc	458657	2030	3	0.09	0.053	19.99	5.867	0.64	0.251	74.85	5.580	0.55	0.154	0.03	0.001	0.03	0.019	0.01	0.004	0.02	0.002	48.92	28.81	99.09	0.594	0.406	667	–2.52
UZb	458658	2030	1	0.05		19.07		0.57		76.18		0.35		0.04				0.01		0.03		48.29	30.99	99.40	0.563	0.437	633	–2.81
Uzb	87.7	2004	1	0.10		28.17		0.57		66.66		0.45		0.03		0.01		0.01		0.03		56.06	11.77	97.19	0.845	0.155	946	–1.67
UZb	107.7	1984	2	0.56		10.83		2.93		82.03		0.17		0.02		0.02		0.02				42.44	43.98	100.98	0.372	0.628	637	–1.22
UZb	149.8	1942	3	0.09	0.067	27.03	3.448	1.25	0.389	69.36	3.577	0.51	0.009	0.06	0.000	0.01	0.009	0.03	0.003	0.03	0.046	55.83	15.03	99.86	0.817	0.183	930	–1.37
UZb	210.9	1881	2	0.08		5.49		1.75		87.09		0.14		0.03		0.02				0.02		36.41	56.31	100.26	0.175	0.825	532	–0.39
UZb	249.2	1843	4	0.21	0.292	10.06	1.390	2.24	0.272	83.90	1.361	0.22	0.020			0.02						41.25	47.39	101.38	0.326	0.674	693	–0.21
UZb	290.8	1801	2	0.03		8.73		2.09		85.57		0.21		0.05		0.02						39.80	50.85	101.78	0.278	0.722	660	–0.10
UZb	344.1	1748	3	0.07	0.013	13.02	0.656	2.32	0.223	80.80	0.411	0.24	0.028	0.13	0.031	0.01	0.008	0.02		0.03		43.40	41.55	100.81	0.421	0.579	662	–1.34
UZb	401.3	1691	2	0.10		11.91		2.98		80.27		0.25		0.25		0.01		0.01		0.06		42.09	42.43	100.08	0.402	0.598	617	–1.82
UZb	461.8	1630	2	0.07		15.08		2.98		75.51		0.31		0.21				0.01		0.02		44.30	34.68	97.65	0.520	0.480	714	–1.34
UZb	491.8	1600	3	0.07	0.029	19.58	1.419	2.88	0.206	73.86	1.542	0.32	0.059	0.38	0.038	0.02	0.001	0.02	0.003	0.03	0.043	48.86	27.77	99.93	0.646	0.354	738	–1.70
UZa	555.5	1536	4	0.06	0.019	12.91	0.599	3.29	0.463	77.95	0.533	0.27	0.045	0.32	0.135	0.01	0.004	0.02	0.007			42.54	39.35	98.76	0.448	0.552	701	–1.04
UZa	585.5	1506	1	0.03		12.19		2.90		79.77		0.23		0.08				0.02				42.37	41.56	99.37	0.415	0.585	706	–0.75
UZa	648.4	1443	2	0.06		12.22		3.35		80.67		0.24		0.37		0.03		0.04		0.07		42.55	42.35	101.28	0.413	0.587	713	–0.65
UZa	689.1	1403	3	0.09	0.031	12.96	0.904	3.30	0.183	80.13	0.455	0.28	0.046	0.38	0.048	0.02	0.014	0.05	0.017	0.04	0.002	43.28	40.95	101.36	0.436	0.564	725	–0.68
UZa	749.2	1343	1	0.09		12.30		2.70		80.39		0.15		0.48				0.04				42.30	42.32	100.37	0.405	0.595	723	–0.51
UZa	809.2	1282	3	0.07	0.032	11.50	0.583	3.23	0.355	80.46	0.952	0.19	0.054	0.43	0.122	0.04	0.025	0.07	0.013	0.02	0.002	41.58	43.21	100.33	0.391	0.609	646	–1.30
UZa	854.5	1233	4	0.05	0.073	17.04	2.291	3.35	0.499	74.12	0.484	0.31	0.093	0.48	0.156			0.07	0.027	0.04		46.01	31.23	98.59	0.587	0.413	683	–1.90
UZa	903.8	1188	3	0.15	0.027	13.64	0.417	2.91	0.245	78.51	0.568	0.25	0.029	0.56	0.112	0.01	0.000	0.09	0.012	0.07	0.068	43.28	39.15	100.10	0.454	0.546	713	–0.86
UZa	941.8	1150	1	0.06		15.72		3.47		76.15		0.39		0.60		0.01		0.10		0.06		44.96	34.66	100.02	0.535	0.465	844	0.47
MZ	458264	1060	1	0.04		12.77		3.73		80.23		0.34		0.29		0.03		0.17				43.32	41.01	101.68	0.439	0.561	943	0.70
MZ	458263	1055	3	0.04	0.052	14.80	0.523	3.54	0.102	77.16	0.757	0.25	0.047	0.64	0.130	0.01	0.011	0.17	0.022	0.05	0.070	44.27	36.55	100.32	0.505	0.495	832	–0.07
MZ	458262	1053	3	0.04	0.055	8.46	1.231	3.25	0.330	82.85	0.393	0.28	0.022	0.73	0.098	0.02	0.018	0.16	0.028	0.01	0.012	38.32	49.47	100.73	0.283	0.717	700	0.27
MZ	458260	1024	5	0.12	0.055	14.30	0.825	3.18	0.132	78.84	1.269	0.28	0.038	0.77	0.175	0.02	0.021	0.13	0.033	0.03	0.056	44.01	38.69	101.53	0.472	0.528	852	0.21
MZ	458259	1010	3	0.08	0.052	13.13	0.276	3.33	0.051	79.47	1.229	0.34	0.001	0.61	0.029	0.01	0.018	0.14	0.022	0.02	0.031	42.98	40.54	101.19	0.440	0.560	757	–0.40
MZ	458258	1009	2	0.09		12.69		3.53		79.22		0.29		0.91				0.26				42.23	41.10	101.09	0.428	0.572	725	–0.59
MZ	458255	1002	1	0.06		15.12		3.49		78.26		0.21		0.94				0.13		0.25		44.56	37.44	102.19	0.499	0.501	748	–0.83
MZ	458254	988	2	0.05		14.33		3.84		78.39		0.25		0.88		0.01		0.22		0.08		43.99	38.21	101.87	0.486	0.514	790	–0.32
MZ	458253	984	2	0.36		12.53		3.28		80.95		0.25		0.81		0.02		0.10		0.03		42.98	42.18	102.56	0.415	0.585	771	–0.11
MZ	458251	953	5	0.03	0.037	16.74	0.332	3.62	0.132	76.25	0.368	0.38	0.096	0.97	0.062	0.00	0.004	0.16	0.013	0.05	0.066	45.85	33.78	101.59	0.558	0.442	848	–0.23
MZ	458250	935	9	0.05	0.018	12.77	0.865	3.49	0.301	78.86	0.595	0.31	0.060	0.82	0.103	0.01	0.021	0.21	0.051	0.05	0.043	42.16	40.77	100.66	0.432	0.568	688	–1.11
MZ	458249	930	7	0.05	0.049	13.43	1.464	3.68	1.010	76.89	1.032	0.32	0.115	0.89	0.286	0.02	0.016	0.23	0.120	0.08	0.059	42.28	38.45	99.42	0.464	0.536	681	–1.36
MZ	458247	920	1	0.14		10.25		3.59		81.63		0.27		0.52		0.01		0.50		0.06		40.71	45.47	101.50	0.353	0.647	667	–0.75
MZ	458289	890	4	0.05	0.010	12.42	0.841	3.79	0.055	81.19	1.170	0.34	0.042	0.98	0.115	0.01	0.017	0.40	0.044	0.08	0.088	42.48	43.01	103.56	0.412	0.588	818	0.42
MZ	458288	877	3	0.03	0.012	13.23	0.329	3.71	0.126	79.74	0.557	0.31	0.057	0.76	0.116	0.03	0.033	0.43	0.048	0.05	0.067	43.19	40.60	102.35	0.446	0.554	835	0.26
MZ	458287	875	2	0.02		13.25		3.71		76.17		0.27		0.80				0.21		0.07		41.94	38.04	98.29	0.466	0.534	855	–0.39
MZ	458286	847	2	0.06		11.83		3.69		77.80		0.24		0.93				0.26		0.14		40.67	41.26	99.08	0.411	0.589	682	–1.03
LZc	458285	830	3	0.04	0.040	10.75	1.005	3.33	0.272	81.67	0.723	0.25	0.028	0.83	0.110		0.000	0.24	0.014	0.04	0.053	40.63	45.60	101.70	0.357	0.643	711	–0.31
LZc	458284	816	3	0.03	0.012	16.18	0.269	3.78	0.347	75.54	0.428	0.37	0.047	1.56	0.257	0.01	0.005	0.39	0.009	0.07	0.084	44.37	34.64	101.39	0.539	0.461	723	–1.24
LZc	458283	808	2	0.05		10.21		3.72		79.41		0.21		0.80				0.50		0.04		39.58	44.26	99.36	0.358	0.642	724	–0.22
LZc	458281	798	3	0.01	0.011	15.14	0.426	4.16	0.349	73.90	1.993	0.38	0.091	1.51	0.134	0.01	0.018	0.25	0.033	0.06	0.046	42.73	34.64	98.89	0.528	0.472	893	0.29
LZc	458282	798	2	0.07		14.93		4.54		76.66		0.33		1.48				0.22		0.07		43.74	36.57	101.95	0.515	0.485	827	–0.14
LZc	458210	742	1	0.02		6.91		3.75		81.90		0.17		0.96				0.98		0.05		36.40	50.55	99.81	0.242	0.758	619	–0.25
LZc	458278	710	2			12.75		3.70		79.78		0.29		0.59				1.11		0.08		43.03	40.83	102.39	0.437	0.563	866	0.54
LZc	458277	703	4	0.02	0.027	13.19	1.240	3.67	0.298	78.07	2.085	0.27	0.086	0.91	0.188	0.02	0.016	1.72	0.301	0.15	0.166	42.76	39.23	101.93	0.453	0.547	799	0.00
LZb	458201	488	1	0.07		7.11		3.82		83.35		0.45		0.68		0.05		0.92		0.01		37.34	51.12	101.57	0.247	0.753	725	0.90
LZb	458231	367	3	0.04		5.70		4.08		87.34		0.19		0.94				0.51		0.17		36.72	56.24	104.61	0.191	0.809	690	1.22
LZb	458226	294	1			3.10		3.18		86.54		0.15		1.10		0.01		1.70		0.27		33.01	59.47	102.00	0.102	0.898	555	1.22
LZb	458225	221	1	0.11		2.36		3.90		83.08		0.09		1.13		0.06		1.53		0.14		31.48	57.34	98.14	0.085	0.915	539	1.39
LZb	458220	173	1	0.09		5.31		2.85		86.89		0.20		0.48				0.37		0.05		36.19	56.33	101.87	0.175	0.825	736	1.97
LZa	458218	159	1	0.14		5.80		2.83		83.80		0.21		0.78		0.05		0.32		0.05		35.40	53.78	99.37	0.194	0.806	644	0.76
LZa	458215	115	1	0.02		4.80		4.49		83.51		0.15		1.15				0.32		0.12		34.29	54.69	100.03	0.171	0.829	698	1.58
LZa	458213	84	1	0.03		5.78		2.22		83.12		0.21		0.40		0.01		0.28		0.27		35.02	53.44	97.66	0.191	0.809	686	1.06
LZa	458212	54	1	0.08		4.81		1.63		84.49		0.13		0.45		0.01		0.59		0.26		34.21	55.87	98.05	0.153	0.847	598	0.81
Ilmenite
Zone	Sample ID	Stratigraphic height	n	SiO2		TiO2		Al2O3		FeO*		MnO		MgO		CaO		Cr2O3		NiO		FeO	Fe2O3	Total	XHe	XIl
		(m)		Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD
UZc	458636	2165	3	0.01	0.005	50.76	0.573	0.02	0.012	49.01	0.509	0.97	0.18	0.03	0.043			0.01	0.000	0.06	0.023	43.68	4.82	99.64	0.047	0.953
UZc	458637	2164	1	0.01		50.36		0.04		48.02		0.68								0.04		45.49	3.91	100.04	0.037	0.963
UZc	458638	2163	4	0.04	0.009	50.11	0.769	0.02	0.013	49.01	0.716	0.39	0.03	0.02	0.033	0.02	0.000	0.02	0.000	0.02	0.000	44.20	4.80	100.36	0.046	0.954
UZc	458639	2162	3	0.04	0.006	50.54	0.403	0.03	0.032	48.52	0.448	0.69	0.07			0.03	0.000	0.03	0.000			44.65	4.17	100.41	0.040	0.960
UZc	458640	2160	4	0.02	0.003	51.01	0.456	0.03	0.011	48.40	0.274	0.48	0.08	0.02	0.034	0.02	0.000	0.02	0.000			45.20	3.37	99.61	0.032	0.968
UZc	458642	2155	4	0.03	0.006	50.44	0.202	0.02	0.015	48.23	0.408	0.43	0.13	0.01	0.043	0.06	0.003	0.01	0.000	0.04	0.000	46.13	3.89	101.66	0.036	0.964
UZc	458643	2150	3	0.05	0.003	50.57	0.145	0.01	0.001	49.64	0.317	0.90	0.12	0.03	0.023	0.01	0.000			0.06	0.000	42.66	5.47	99.89	0.054	0.946
UZc	458644	2147	2			50.93		0.03		47.58		0.76		0.01		0.01				0.03	0.000	46.03	2.95	101.39	0.028	0.972
UZc	458645	2144	3			51.35	0.221	0.01	0.002	48.68	0.131	0.94	0.10	0.04	0.036	0.04	0.006	0.01	0.000	0.03	0.000	44.53	3.95	100.20	0.038	0.962
UZc	458646	2144	3	0.03	0.029	49.90	0.380	0.01	0.002	48.09	0.100	1.72	0.29			0.03	0.006	0.02	0.000	0.01	0.000	43.38	5.55	100.89	0.053	0.947
UZc	458657	2030	2	0.07		50.81		0.01		48.38		1.00		0.02	0.043	0.01	0.008	0.01	0.000	0.03	0.000	43.49	4.00	101.01	0.039	0.961
UZb	458658	2030	2	0.17		50.56		0.10		48.34		0.88				0.05		0.01	0.000			43.14	3.90	99.06	0.039	0.961
UZb	87.7	2004	1	0.13		50.97		0.03		46.65		0.89		0.01								46.42	1.81	100.38	0.017	0.983
UZb	107.7	1984	5	0.07	0.046	50.98	0.437	0.15	0.217	48.05	0.223	0.77	0.12	0.11	0.070	0.03	0.003	0.03	0.002	0.02	0.029	45.24	3.53	100.45	0.034	0.966
UZb	149.8	1942	3	0.02	0.036	50.47	0.137	0.05	0.041	48.41	0.377	0.99	0.09	0.04	0.043	0.02	0.002	0.02	0.000	0.07	0.000	43.83	4.60	100.06	0.045	0.955
UZb	210.9	1881	4	0.02	0.017	50.59	0.178	0.04	0.007	47.98	0.514	0.83	0.05	0.09	0.105	0.01	0.003	0.02	0.000	0.03	0.020	45.53	3.97	100.89	0.037	0.963
UZb	249.2	1843	6	0.35	0.551	49.82	0.778	0.12	0.071	49.10	0.558	0.72	0.11	0.30	0.207	0.04	0.006	0.01	0.000	0.04	0.032	43.83	5.81	99.95	0.056	0.944
UZb	290.8	1801	4	0.04	0.028	49.27	1.002	0.04	0.015	49.06	0.983	0.62	0.15	0.24	0.152	0.01	0.000	0.03	0.002	0.07	0.000	42.87	6.44	100.52	0.063	0.937
UZb	344.1	1748	4	0.03	0.019	50.01	0.408	0.09	0.039	48.66	0.147	0.52	0.04	0.46	0.037	0.04	0.005	0.02	0.000	0.05	0.000	42.58	5.53	100.31	0.054	0.946
UZb	401.3	1691	4	0.09	0.091	50.76	0.318	0.09	0.019	47.56	0.286	0.56	0.08	0.65	0.314			0.02	0.007	0.04	0.000	43.26	3.90	99.06	0.038	0.962
UZb	461.8	1630	6	0.03	0.022	50.35	0.305	0.09	0.017	46.77	0.633	0.50	0.06	0.87	0.210	0.03	0.003	0.01		0.03	0.000	43.49	4.01	99.76	0.039	0.961
UZb	491.8	1600	3	0.04	0.028	50.77	0.377	0.08	0.037	47.09	0.218	0.46	0.07	0.87	0.062	0.01	0.000	0.01		0.02	0.000	43.39	3.81	99.91	0.037	0.963
UZa	555.5	1536	6	0.02	0.018	50.96	0.351	0.08	0.017	46.82	0.399	0.52	0.05	1.03	0.109	0.01	0.006	0.01	0.007	0.07	0.000	44.09	3.86	99.36	0.037	0.963
UZa	585.5	1506	5	0.04	0.012	50.17	0.348	0.08	0.050	47.56	0.829	0.90	0.17	0.16	0.111	0.03	0.006	0.02	0.000	0.03	0.026	44.70	4.13	101.29	0.039	0.961
UZa	648.4	1443	3	0.06	0.027	50.83	0.456	0.06	0.067	48.42	0.625	0.56	0.07	0.88	0.172	0.01	0.000	0.02	0.003	0.03	0.026	43.55	5.36	100.75	0.051	0.949
UZa	689.1	1403	3	0.03	0.017	50.16	0.400	0.08	0.009	48.37	0.403	0.51	0.06	0.97	0.005	0.02	0.001	0.02	0.004	0.05	0.023	42.16	6.07	100.17	0.059	0.941
UZa	749.2	1343	3	0.13	0.130	50.14	0.581	0.19	0.244	47.62	0.146	0.52	0.01	0.91	0.157	0.04	0.005	0.01	0.000			43.43	5.14	100.24	0.049	0.951
UZa	809.2	1282	3	0.02	0.000	49.99	0.038	0.07	0.019	48.06	0.528	0.61	0.14	0.93	0.140	0.01	0.000	0.02	0.000	0.03	0.000	40.96	5.76	99.34	0.058	0.942
UZa	854.5	1233	4	0.02	0.007	50.90	0.556	0.05	0.024	46.15	0.434	0.56	0.08	1.02	0.151			0.02	0.000	0.02	0.000	44.90	3.19	100.71	0.030	0.970
UZa	903.8	1188	3	0.03	0.007	50.75	0.316	0.08	0.060	47.77	0.127	0.52	0.08	1.20	0.151	0.02	0.005	0.01	0.000			42.68	5.31	100.33	0.051	0.949
UZa	941.8	1150	4	0.01	0.013	50.48	0.393	0.07	0.016	47.45	0.431	0.57	0.09	1.17	0.132	0.02	0.007	0.02	0.012	0.02	0.000	43.42	5.35	102.77	0.051	0.949
MZ	458264	1060	4	0.01	0.010	50.66	0.268	0.07	0.038	49.11	0.720	0.48	0.14	0.92	0.324	0.01	0.014	0.03	0.055	0.05	0.066	46.34	6.82	100.73	0.061	0.939
MZ	458263	1055	6	0.04	0.068	44.62	14.265	0.70	1.429	52.48	11.992	0.38	0.04	1.73	0.416	0.01	0.013	0.03	0.046	0.05	0.061	32.92	15.82	100.19	0.171	0.829
MZ	458262	1032	4	0.21	0.398	49.17	1.004	0.12	0.117	47.16	0.873	0.44	0.06	1.44	0.171	0.01	0.006	0.01	0.017	0.05	0.051	41.72	6.44	101.19	0.063	0.937
MZ	458260	1024	4	0.02	0.014	49.12	0.623	0.12	0.060	47.52	1.038	0.37	0.07	2.40	0.130	0.01	0.029	0.03	0.018	0.04	0.074	39.64	8.97	101.66	0.088	0.912
MZ	458259	1010	3			50.80	0.098	0.07	0.022	47.71	0.769	0.39	0.02	1.77	0.197					0.01	0.020	42.17	6.23	101.47	0.060	0.940
MZ	458258	1003	8	0.01	0.016	50.88	0.429	0.10	0.080	47.77	0.985	0.46	0.10	1.57	0.208	0.01	0.010	0.02	0.020	0.02	0.028	42.24	5.86	98.79	0.057	0.943
MZ	458255	1002	2	0.02		51.30		0.05		47.09		0.52		2.00		0.01		0.06		0.09		41.70	5.66	100.03	0.055	0.945
MZ	458254	988	1			49.96		0.08		46.80		0.53		2.01		0.01		0.06				40.75	6.67	100.50	0.066	0.934
MZ	458253	961	2	0.01		50.18		0.27		46.75		0.44		2.12				0.06				41.53	6.61	102.26	0.064	0.936
MZ	458251	953	5	0.02	0.026	49.38	0.492	0.10	0.049	49.23	0.381	0.42	0.06	2.07	0.136			0.07	0.027	0.02	0.036	38.22	9.41	102.43	0.096	0.904
MZ	458250	935	7	0.08	0.181	51.96	0.647	0.10	0.057	46.69	0.433	0.52	0.11	2.07	0.087	0.02	0.020	0.01	0.015	0.04	0.073	42.50	4.60	101.56	0.044	0.956
MZ	458249	930	8	0.05	0.090	51.78	0.552	0.06	0.028	46.64	0.734	0.45	0.10	2.08	0.204			0.01	0.020	0.03	0.043	41.94	4.62	101.25	0.045	0.955
MZ	458247	920	8	0.01	0.011	52.16	0.531	0.09	0.095	46.10	0.665	0.46	0.04	1.85	0.153	0.01	0.015	0.06	0.062	0.04	0.068	44.66	3.45	98.90	0.032	0.968
MZ	458289	890	2	0.05		48.15		0.13		47.76		0.56		1.59		0.05		0.24	0.003	0.04		40.14	8.84	102.77	0.087	0.913
MZ	458288	877	3	0.02	0.025	50.52	1.005	0.08	0.006	48.10	0.358	0.60	0.08	2.38	0.120			0.14	0.011	0.03	0.022	41.29	8.52	102.06	0.081	0.919
MZ	458287	875	3	0.01	0.003	49.28	0.965	0.11	0.035	48.95	0.402	0.44	0.08	2.23	0.100			0.15	0.004	0.04	0.073	37.14	9.42	100.12	0.098	0.902
MZ	458286	847	2	0.02		50.98		0.12		45.62		0.43		1.97		0.01		0.01		0.02		42.25	4.18	100.31	0.041	0.959
LZc	458285	830	3	0.03	0.011	50.94	0.849	0.09	0.017	46.01	0.603	0.39	0.07	2.36	0.041			0.00	0.005	0.06	0.094	42.03	5.47	102.10	0.053	0.947
LZc	458284	816	3	0.15	0.248	51.36	0.688	0.16	0.215	46.95	1.453	0.47	0.09	2.34	0.213	0.06	0.068	0.02	0.017	0.04	0.035	40.29	5.76	102.31	0.058	0.942
LZc	458283	808	3	0.02	0.015	52.22	0.199	0.22	0.183	45.48	0.778	0.44	0.03	3.14	0.161	0.02	0.026	0.16	0.028	0.03	0.032	42.47	5.30	97.77	0.050	0.950
LZc	458281	798	2	0.05		47.07		0.14		47.25		0.45		2.12		0.04		0.11				35.89	9.58	100.16	0.102	0.898
LZc	458282	752	3	0.01	0.012	50.89	1.037	0.07	0.002	44.51	1.497	0.43	0.05	3.26	0.200			0.00	0.000	0.03	0.060	41.12	5.81	102.50	0.056	0.944
LZc	458210	723	2	0.08		51.08		0.09		48.43		0.54		2.04				0.16		0.08		40.39	7.16	99.03	0.071	0.929
LZc	458278	710	7	0.05	0.052	48.83	0.312	0.21	0.306	48.40	0.469	0.39	0.06	2.62	0.110	0.01	0.016	0.09	0.035	0.07	0.054	39.06	10.70	101.96	0.104	0.896
LZc	458277	681	2	0.20		49.34		0.51		48.69		0.47		1.45		0.05		0.15		0.02		40.89	7.93	101.49	0.078	0.922
LZb	458201	424	2	0.01		47.07		0.11		49.73		0.45		2.04				0.20				36.35	12.15	101.46	0.125	0.875
LZb	458231	367	4	0.02	0.029	48.02	0.351	0.16	0.088	49.84	0.755	0.38	0.10	2.49	0.230	0.02	0.022	0.27	0.018	0.06	0.089	37.21	12.46	101.44	0.124	0.876
LZb	458226	294	3	0.01	0.022	48.38	1.518	0.06	0.050	48.43	1.541	0.52	0.13	2.49	0.180	0.02	0.020	0.20	0.003	0.08	0.070	36.75	10.60	100.22	0.109	0.891
LZb	458225	175	1	0.04		48.96		0.14		46.29		0.28		3.05		0.05		0.15		0.19		38.13	9.11	97.60	0.091	0.909
LZb	458220	161	1			43.11		0.09		46.67		0.32		2.33		0.01		0.27		0.08		35.77	14.49	97.60	0.146	0.854
LZa	458218	125	2			48.11		0.11		47.02		0.46		2.49				0.09		0.09		37.50	9.52	98.20	0.097	0.903
LZa	458215	107	4	0.05	0.044	45.05	2.120	0.23	0.206	47.65	0.993	0.42	0.10	2.59	0.080			0.20	0.04	0.03	0.022	34.96	13.29	97.03	0.138	0.862
LZa	458213	84	2			47.68		0.05		45.25		0.40		2.86		0.01		0.06		0.09		38.96	9.26	97.47	0.091	0.909
LZa	458212	54	2	0.01		47.21		0.06		47.29		0.39		1.40		0.01		0.14		0.04		38.90	8.50	100.14	0.087	0.913
n: number of individual mineral analyses used for each calculated average (Ave.) with 1σ SD where n > 2. FeO*, total iron as FeO. Iron is redistributed between FeO and Fe2O3 based on charge balance (magnetite, 3 cations and 4 oxygens ; ilmenite 2 cations and 3 oxygens). XIl: mole fraction of ilmenite. XHe: mole fraction of hematite. XUlv: mole fraction of ulvöspinel. XMt: mole fraction of magnetite. Temperature (°C) and oxygen fucacity (logfO2 NNO) for coexisting oxide minerals are based on Ghiorso & Evans (2008). Stratigraphic height is given as high and low referring to the interval used for averaging. Data available in Supplementary File S1.

4.3.7 Apatite

Apatite first occurs in UZb (Fig. 11) as an early crystallising primocryst. Throughout the LS, apatite appears as a later interstitial phase (Nash 1976; Holness et al. 2011; Pedersen et al. 2021) and in late-forming pegmatitic veins (Nash 1976; Brown & Peckett 1977; Larsen 1992; Sonnenthal 1992; Larsen & Brooks 1994). The analysed apatite (n = 164) is fundamentally composed of Ca (9.693 pfu) and P (5.767 pfu) with small amounts of Si (0.044 pfu), Fe (0.057 pfu) and Mn (0.006 pfu) calculated to 26 anions (O,F,Cl,OH; Table 10; Fig. 24B). Thus, the calculated average formulae Ca_9.67P_5.81O₂₄(F,Cl,OH)₂ is relatively close to ideal apatite of Ca₁₀P₆O₂₄(F,Cl,OH)₂ and not dissimilar to the data of Nash (1976) and Brown & Peckett (1977). The measured F- and Cl-monovalent anions and the balance-calculated OH in the apatite structure vary as a function of stratigraphic position. A mixture of (F+Cl+OH) occurs in the LZ, MZ and UZa. In UZb, (F+OH) occurs where apatite becomes an early-forming mineral phase, and in UZc it becomes nearly dry (only F remaining; Fig. 24B). This variation in the anion content indicates the exsolution of a Cl-rich vapour phase as suggested by Sonnenthal (1992) and McBirney (1995) at the base of the UZ and a second OH-vapour boiling in UZc as evident at lower levels and also in studies of pegmatitic veins (Larsen & Brooks 1994). Further detailed studies are, however, needed to unravel these implications beyond the present study of the near liquidus relations (cf. Pedersen et al. 2021).

Table 10 Representative apatite compositions

Zone	Stratigraphic height	n	SiO2 (wt%)		FeO (wt%)		MnO (wt%)		CaO (wt%)		P2O5 (wt%)		Total (wt%)	F (wt%)		Cl (wt%)		Atomic Monovalent Anions
																		F		Cl		OH		Sum	Cl/F
	(m)		Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD		Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD
UBS	2168	3	0.33	0.022	0.34	0.166	0.01	0.000	54.92	0.525	41.67	0.159	97.27	3.86	0.202	0.06	0.030	1.982	0.087	0.016	0.008	0.002	0.006	2.000	0.008
UZc	2165	1	0.36		0.30		0.02		54.89		40.85		96.41	3.71		0.15		1.929		0.043		0.029		2.000	0.022
UZc	2164	2	0.53		0.55		0.03		54.68		41.42		97.21	3.75		0.07		1.927		0.020		0.053		2.000	0.010
UZc	2163	3	0.35	0.001	0.42	0.019	0.01	0.000	54.60	1.331	41.67	0.679	97.05	3.71	0.019	0.08	0.011	1.912	0.043	0.021	0.003	0.067	0.041	2.000	0.011
UZc	2162	3	0.30	0.012	0.27	0.115	0.06	0.035	54.58	0.503	41.72	0.135	96.92	3.64	0.060	0.08	0.015	1.880	0.033	0.023	0.004	0.096	0.034	2.000	0.012
UZc	2160	6	0.28	0.022	0.34	0.071	0.03	0.024	54.63	0.325	41.57	0.288	96.85	3.75	0.091	0.10	0.011	1.934	0.043	0.026	0.003	0.040	0.038	2.000	0.014
UZc	2159	4	0.37	0.074	0.47	0.091	0.05	0.025	54.18	0.309	41.84	0.127	96.89	3.64	0.060	0.09	0.019	1.875	0.031	0.026	0.005	0.099	0.031	2.000	0.014
UZc	2155	3	0.36	0.285	0.59	0.160	0.03	0.002	54.40	0.476	41.27	0.393	96.66	3.78	0.049	0.04	0.023	1.956	0.031	0.012	0.006	0.032	0.037	2.000	0.006
UZc	2150	1	0.30		0.62		0.03		55.46		41.98		98.39	4.08		0.12		2.063		0.032				2.095	0.015
UZc	2147	5	0.23	0.058	0.37	0.144	0.04	0.023	55.22	0.302	42.14	0.296	98.00	3.82	0.085	0.10	0.029	1.944	0.039	0.026	0.008	0.030	0.048	2.000	0.014
UZc	2144	4	0.24	0.152	0.51	0.108	0.02	0.025	55.26	0.592	41.83	0.325	97.87	3.88	0.128	0.13	0.018	1.979	0.049	0.035	0.005			2.014	0.018
UZc	2144	4	0.28	0.067	0.31	0.051	0.03	0.014	54.54	0.552	41.72	0.090	96.87	3.72	0.048	0.09	0.024	1.919	0.020	0.023	0.007	0.057	0.024	2.000	0.012
UZc	2141	5	0.38	0.200	0.36	0.097	0.03	0.018	55.11	0.798	41.54	0.392	97.43	3.75	0.068	0.16	0.061	1.924	0.026	0.045	0.017	0.030	0.018	2.000	0.024
UZc	2119	3	0.11	0.060	0.41	0.006	0.02	0.000	54.60	0.828	42.23	0.492	97.37	3.87	0.068	0.07	0.000	1.976		0.019		0.004		2.000	0.010
UZc	2075	4	0.13	0.018	0.32	0.044	0.05	0.029	55.62	0.467	42.57	0.200	98.69	3.58	0.213	0.08	0.020	1.821	0.103	0.021	0.005	0.158	0.107	2.000	0.011
UZc	2060	3	0.21	0.074	0.40	0.061	0.04	0.007	54.79	0.408	41.49	0.282	96.92	3.73	0.207	0.12	0.031	1.928	0.110	0.032	0.008	0.040	0.066	2.000	0.017
UZc	2046	1	0.12		0.49		0.10		56.42		44.95		102.09	4.01		0.03		1.949		0.007		0.043		2.000	0.004
UZb	2032	3	0.35	0.159	0.71	0.285	0.08	0.023	55.37	0.211	41.84	0.273	98.34	3.68	0.073	0.05	0.006	1.881	0.031	0.014	0.002	0.105	0.032	2.000	0.007
UZb	2030	2	0.28		0.45		0.05		54.38		41.69		96.85	3.61		0.14		1.867		0.038		0.095		2.000	0.020
UZb	2004	3	0.13	0.042	0.33	0.078	0.04	0.039	54.79	0.560	41.09	0.794	96.38	3.91	0.112	0.09	0.005	2.025	0.031	0.026	0.002			2.051	0.013
UZb	1984	6	0.31	0.144	0.61	0.177	0.06	0.028	56.68	0.415	41.40	0.238	99.06	1.58	0.350	0.07	0.009	0.840	0.180	0.020	0.002	1.140	0.181	2.000	0.024
UZb	1942	3	0.25	0.093	0.45	0.053	0.05	0.012	56.56	0.142	41.56	0.103	98.87	2.14	0.425	0.11	0.030	1.126	0.214	0.032	0.009	0.843	0.205	2.000	0.028
UZb	1881	6	0.28	0.135	0.34	0.172	0.05	0.036	54.81	0.378	40.75	0.896	96.23	3.94	0.120	0.07	0.012	2.044	0.075	0.018	0.003			2.063	0.009
UZb	1843	5	0.32	0.135	0.37	0.172	0.07	0.000	57.18	0.850	41.60	0.786	99.53	1.90	0.127	0.07	0.000	0.997		0.019		0.984		2.000	0.019
UZb	1801	6	0.16	0.041	0.28	0.105	0.08	0.047	55.41	0.855	44.37	0.796	100.30	3.90	0.043	0.07	0.015	1.929	0.041	0.017	0.004	0.054	0.039	2.000	0.009
UZb	1748	6	0.18	0.036	0.51	0.111	0.06	0.029	56.57	0.982	38.27	0.698	95.60	1.35	0.248	0.07	0.021	0.757	0.129	0.021	0.007	1.221	0.127	2.000	0.028
UZb	1691	8	0.13	0.076	0.26	0.211	0.03	0.000	55.12	0.882	41.34	0.558	96.89	3.96	0.358	0.06	0.000	2.037		0.017				2.054	0.008
UZb	1630	6	0.14	0.051	0.29	0.062	0.05	0.021	54.46	0.502	41.38	0.265	96.33	3.85	0.088	0.06	0.008	1.993	0.045	0.017	0.002			2.010	0.009
LZb	634	1	0.12		0.33		0.05		54.73		42.59		97.82	2.55		0.41		1.324		0.115		0.561		2.000	0.087
LZb	177	3	0.14	0.014	0.27	0.005	0.05	0.061	55.08	0.620	41.69	0.384	97.23	2.42	1.405	0.84	0.066	1.271	0.097	0.235	0.021	0.494	0.118	2.000	0.185
LZb	175	1	0.29		0.57		0.07		55.07		40.76		96.76	2.42		0.75		1.279		0.212		0.509		2.000	0.166
LZa	115	4	0.17	0.096	0.20	0.019	0.09	0.044	54.67	0.545	41.23	0.214	96.36	2.72	0.135	0.46	0.009	1.436	0.079	0.130	0.003	0.434	0.082	2.000	0.090
n: number of analyses used for each average (Ave.) with 1σ SD for n > 2.

4.3.8 Biotite

Mica appears as a late crystallising phase in the LZa and LZb in interstitial patches often coexisting with FeTi oxides and apatite. This mica is a biotite, intermediate between phlogopite and annite with Mg/(Mg+Fe²⁺) ratios between 0.72 and 0.52 (Table 11; Fig. 24C) and with low contents of Al^vi and Fe³⁺, both assumed to fill the T-sites (calculated to 22 oxygens). Although the contents of F and Cl were not analysed, Nash (1976) determined the monovalent anions in the Skaergaard biotite to be dominantly hydroxyl with F/(F+OH) ratios of c. 0.1 and little or no Cl.

Table 11 Individual and average mica compositions

Zone	Sample ID	Hight (m)	n	SiO2 (wt%)	TiO2 (wt%)	Al2O3 (wt%)	FeO (wt%)	MnO (wt%)	MgO (wt%)	CaO (wt%)	Na2O (wt%)	K2O (wt%)	Total (wt%)	Atomic ratio
														Mg/(Fe+Mg)
LZb	458206	634	1	36.93	5.16	12.73	20.47	0.22	12.09	0.21	0.20	7.98	95.99	0.513
LZb	458221	175	3	35.80	4.59	13.08	15.69	0.03	13.85	0.02	0.15	8.67	91.88	0.612
LZa	458219	161	1	37.18	4.41	13.74	11.21		16.75		0.27	8.73	92.27	0.727
LZa	458215	115	1	36.42	3.64	14.96	11.56	0.06	16.83	0.08	0.27	8.45	92.26	0.722
LZa	458213	84	2	37.14	4.35	13.80	14.05	0.05	15.40		0.36	8.46	93.62	0.661
LZa	458211	7	2	37.46	4.21	14.81	12.11	0.02	17.48	0.06	0.32	8.23	94.70	0.720
Individual and averages of mica when detected. n: number of analyses used for calculating averages.

4.4 Cryptic mineral variations

The silicate and FeTi oxide primocrysts show systematic compositional variation as a function of stratigraphic position through the LS (Table 12), most noticeably in the Mg/(Mg+Fe) ratios of the mafic minerals and the Ca/(Ca+Na) ratio of plagioclase. This ‘hidden’ compositional variation has been referred to as cryptic variation or layering (Wager & Deer 1939; Wager & Brown 1967; Irvine 1982; McBirney 1989a). Cryptic variation has widely been seen as related to variations in liquidus temperature and parental-magma compositions resulting from fractional crystallisation or other types of compositional changes in a closed or partially open magma chamber. Corresponding cryptic mineral trends are observed in the MBS and UBS (e.g. Salmonsen & Tegner 2013).

Table 12 Summary of cryptic primocryst compositions

Zone	Stratigraphic height (m)		Plagioclase				Olivine				High-Ca Pyroxene				Low-Ca Pyroxene
			Ave.	SD	Min.	Max.	Ave.	SD	Min.	Max.	Ave.	SD	Min.	Max.	Ave.	SD	Min.	Max.
	high	low	An	An (1σ)	An	An	Fo	Fo (1σ)	Fo	Fo	Mg#	Mg# (1σ)	Mg#	Mg#	Mg#	Mg# (1σ)	Mg#	Mg#
UBS	2169	2165	24.7	1.55	23.2	26.3	0.8	0.19	0.6	1.0	8.9	3.00	5.9	11.9
UZc	2165	2165	27.2	1.23	25.9	28.4	0.1	2.26	0.0	2.4	0.2	0.30	0.0	0.5
UZc	2165	2164	28.8	0.90	27.9	29.7	0.2	0.28	0.0	0.5	0.3	0.20	0.1	0.5
UZc	2163	2147	27.4	1.37	26.1	28.8	0.2	0.03	0.1	0.2	0.3	0.30	0.0	0.6
UZc	2144	2141	29.2	1.20	28.0	30.4	0.2	0.04	0.2	0.2	0.6	0.50	0.1	1.1
UZc	2091	2081	32.5	1.55	31.0	34.1	1.1	0.18	1.0	1.3	2.1	0.54	1.6	2.7
UZc	2075	2061	32.3	1.25	31.0	33.5	1.5	0.12	1.4	1.6	4.1	1.00	3.1	5.1
UZc	2060	2046	34.2	1.15	33.1	35.4	2.6	0.31	2.3	3.0	7.6	0.90	6.7	8.5
UZb	2044	2030	30.6	1.10	29.5	31.7	1.3	0.40	0.9	1.7	2.3	0.20	2.1	2.5
UZb	2024	1984	34.4	1.23	33.2	35.7	5.7	0.25	5.4	5.9	14.8	2.30	12.5	17.1
UZb	1962	1921	34.9	1.53	33.4	36.5	9.3	0.60	8.7	9.9	22.9	3.00	19.9	25.9
UZb	1902	1862	35.7	0.97	34.7	36.6	13.4	0.50	12.9	13.9	31.6	1.70	29.9	33.3
UZb	1843	1801	37.2	1.00	36.2	38.2	18.1	0.85	17.3	19.0	36.7	0.80	35.9	37.5
UZb	1782	1748	36.5	0.90	35.6	37.4	22.4	0.80	21.6	23.2	43.6	1.40	42.2	45.0
UZb	1728	1691	38.1	1.10	37.0	39.2	27.2	0.30	26.9	27.5	45.7	0.90	44.8	46.6
UZb	1671	1630	38.2	0.97	37.2	39.2	29.4	0.50	28.9	29.9	49.2	1.20	48.0	50.4	41.0	1.60	39.4	42.6
UZb	1620	1600	39.6	1.05	38.6	40.7	26.2	0.50	25.7	26.7	49.5	1.00	48.5	50.5	33.7
UZa	1561	1527	40.7	0.95	41.7	39.8	28.7	0.35	28.3	29.0	49.7	1.50	48.2	51.2
UZa	1506	1431	41.9	1.35	40.5	43.2	30.8	0.45	30.3	31.2	50.5	1.40	49.1	51.9
UZa	1403	1343	43.4	1.35	42.1	44.8	34.7	0.50	34.2	35.2	53.9	2.30	51.6	56.2	43.8
UZa	1323	1282	43.5	1.47	42.0	45.0	38.6	0.45	38.1	39.0	56.0	1.90	54.1	57.9	46.5	0.90	45.6	47.4
UZa	1268	1237	43.9	2.20	41.7	46.1	37.8	0.60	37.2	38.4	55.7	0.00	55.7	55.7
UZa	1218	1188	44.0	1.75	45.8	42.3	37.5	0.60	36.9	38.1	54.9	1.00	53.9	55.9	47.9	1.40	46.5	49.3
UZa	1178	1131	44.3	1.40	42.9	45.7	39.4	0.60	38.8	40.0	56.5	3.60	52.9	60.1	47.7	0.50	47.2	48.2
MZ	1098	1055	45.1	1.20	43.9	46.3	43.3	0.20	43.1	43.5	57.5	2.39	55.2	59.9	51.8	1.54	50.2	53.3
MZ	1053	1032	46.4	1.65	44.7	48.0					60.2	2.44	57.8	62.6	54.9	2.31	52.6	57.2
MZ	1024	1009	47.0	1.10	45.9	48.1	44.2	0.60	43.6	44.8	59.7	3.56	56.2	63.3	54.1	1.34	52.7	55.4
MZ	1003	1002	47.6	1.73	45.9	49.4					58.7	2.56	56.1	61.3	52.8	2.54	50.2	55.3
MZ	988	961	48.3	1.60	46.7	49.9	48.6	1.00	47.6	49.6	59.0	3.29	55.7	62.3	54.9	1.64	53.3	56.5
MZ	953	930	48.2	1.80	46.4	50.0					61.8	1.96	59.9	63.8	55.0	1.11	53.9	56.1
MZ	921	900	51.9	3.63	48.3	55.6	45.9	0.60	45.3	46.5	60.7	1.64	59.1	62.3	55.3
MZ	890	875	50.0	1.60	48.4	51.6	50.5	0.70	49.8	51.2	62.8	1.77	61.1	64.6
LZc	847	816	50.5	1.70	48.8	52.2	53.9	1.70	52.2	55.6	63.6	2.91	60.7	66.5	59.8
LZc	808	798	49.9	1.53	48.3	51.4	55.1	0.60	54.5	55.7	64.4	1.78	62.6	66.2	58.4
LZc	784	742	50.9	1.67	49.2	52.5					65.3	3.86	61.5	69.2	60.7	0.62	60.1	61.4
LZc	723	703	53.2	1.37	51.9	54.6	52.2	0.45	51.8	52.7	65.1	1.84	63.3	66.9	58.7
LZb	703	681	51.9	1.50	50.4	53.4	51.5	0.45	51.1	52.0	64.6	2.06	62.5	66.6	55.5
LZb	634	580	54.8	1.73	53.1	56.5	49.8	0.40	49.4	50.2	65.4	3.30	62.1	68.7
LZb	558	488	55.3	2.77	52.6	58.1	52.4	0.50	51.9	52.9	65.2	2.25	63.0	67.5	61.7
LZb	447	367	56.4	2.37	54.0	58.8	53.4	0.50	52.9	53.9	65.5	3.33	62.1	68.8	58.0	2.02	56.0	60.0
LZb	346	221	58.9	1.70	57.2	60.6	57.0	0.70	56.3	57.7	68.4	3.78	64.6	72.2	62.9
LZb	177	173	60.2	1.53	58.6	61.7	53.0	0.90	52.1	53.9	68.0	5.23	62.8	73.2	60.8
LZa	161	137	58.1	3.97	54.1	62.0	56.6	0.60	56.0	57.2	70.4	4.59	65.8	75.0	64.9	0.98	63.9	65.9
LZa	125	96	60.3	3.33	56.9	63.6	58.0	0.95	57.1	59.0	70.9	0.91	70.0	71.8	66.7	0.37	66.3	67.0
LZa	84	27	62.0	5.43	56.5	67.4	57.4	2.15	55.2	59.5	71.0	6.20	64.8	77.2	68.4
LZa	7		63.2	5.65	57.5	68.8	61.1	3.60	57.5	64.7	71.6	4.20	67.4	75.8	64.4
Calculated as averages (Ave.) of three consecutive samples with 1σ level SD calculated for n < 2. Min.: minimum. Max.: maximum. Stratigraphic height is given as high and low referring to the interval used for averaging. Complete data set in Supplementary File S1. An and Fo in mol%.

4.4.1 Olivine

The olivine composition shows a systematic upward increase in iron from Fo_61.1±3.6 at the base of LZa to Fo_0.8±0.2 in UZc and the SH (Table 12; Fig. 25). The upward change in Fo content varies systematically from about 2.0% per 100 m of stratigraphy in the LZ to UZa, to 7.3% at the top of UZb. The variation compares to predicted ideal fractional crystallisation trends in a closed basaltic system (Maaløe 1976b; Morse 1996). The noticeably high variability in the LZa and LZb decreases in the MZ and particularly in the UZ is attributable to elevated residual melt content in the lower part of the intrusion (Tegner et al. 2009). A couple of irregularities may be seen first within the LZc as a regression towards higher forsterite when FeTi oxides become dominant, and then again at the UZa to UZb boundary where modal olivine markedly increases. Nwe (1976) and Holness et al. (2015) reported olivine compositions in the HZ up to Fo₆₅, similar to the maximum value noted by McBirney (1989a) in his eastern section. The compositional variation of UBS olivine reverses the LS variation from Fo₀ at the SH to Fo₅₇ at the top of LZ’ (Naslund 1984).

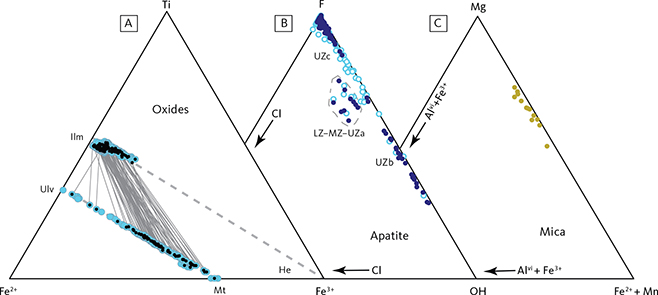
Fig. 24 Compositions of minor mineral components of the LS. A: Ternary Fe²⁺–Ti–Fe³⁺ diagram showing the main molecular components of FeTi oxide solid solutions. The analysed oxides (blue dots) fall along two series approximately defining the ilmenite-hematite and ulvöspinel-magnetite solid solutions (grey dashed line). Ilm: ilmenite. He: hematite. Ulv: ulvöspinel. Mt: magnetite. Tie-lines are shown (grey solid lines) between average compositions (black dots) of the two series for individual thin sections. B: Ternary diagram showing the monovalent Cl–F–OH anion variation in apatite. Solid blue dots: this study. Open blue dots: previously published data (Nash 1976; Brown & Peckett 1977; Larsen 1992). Apatite of the LZ to UZa is Cl-bearing, the apatite of UZb is hydroxyl-bearing, and apatite in the UZc is F-bearing. C: Ternary diagram showing the octahedral (Al^vi + Fe³⁺) – Mg – (Fe²⁺ + Mn) variation in mica (yellow dots). Octahedral alumininum (Al^vi) is calculated assuming that tetrahedral Al and Fe³⁺ with Si filling in the tetrahedral site to an ideal occupancy. The remaining iron is calculated as Fe²⁺. Biotite analysed in this study contains little, if any, Al^vi and Fe³⁺.

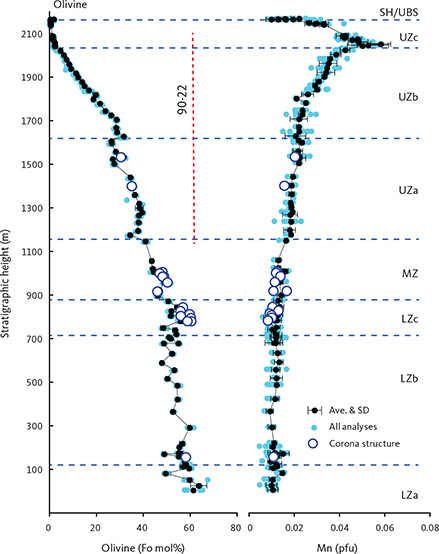
Fig. 25 Cryptic variation of olivine as a function of stratigraphic height (m) in the LS. Shown are forsterite content (Fo mol%) and the numbers of Mn pfu (4 oxygen). Small blue dots: individually analysed points. Solid black dots: average of each thin section with 1s SD. Open blue dots: composition of coronas. Red vertical dashed line: location of drill core 90-22. Blue horizontal dashed lines: divisions of the LS. Abbreviations in Fig. 2. Ave.: average.

The only minor element in olivine that shows a systematic variation with stratigraphic height is manganese, which modestly increases from the base of LZa until the lower part of UZb. It then markedly increases to the base of UZc where it reaches 0.25 pfu, and then decreases to 0.01 pfu at the top of UZc to the same level as the base of LZa (Fig. 25). The average calcium content is 0.10 ± 0.06 (wt% CaO) or 0.003 ± 0.002 (Ca pfu) and shows no detectable variation with stratigraphic height, as also observed by Nwe (1976). The average calcium content of the Skaergaard olivine equals the maximum limit of CaO for plutonic olivine reported by Simkin & Smith (1970).

4.4.2 Plagioclase

The cryptic variation is most noticeable in plagioclase primocrysts that vary from calcic at the base of LZa (An_63.2±5.7) to sodic at the SH of UZc (An_24.7±1.6; Table 12) defining a near linear variation as a function of stratigraphic height (Fig. 26) with a few deviations at the base of the MZ. An unusually high average primocryst An content of 61 was found in a single sample from the lower part of MZ (900 m) that may reflect erroneous sampling of a block from the basaltic roof of the intrusion (McBirney 1989a; Irvine et al. 1998; Sonnenthal & McBirney 1998). The slope of the linear variation in An content is 1.6 An% per 100 m of stratigraphy between An₂₅ and An₆₃ and confirms the findings of previous studies (Fig. 1; Wager & Brown 1967; McBirney 1989a). The plagioclase compositions at the appearance of ferrobustamite are similar (An_32-33) to UBS plagioclase at a corresponding stratigraphic level (Salmonsen & Tegner 2013). The maximum An content of plagioclase in the HZ (c. 65% An) reaches about the same value as found in the LZa (Maaløe 1976a; Holness et al. 2015). There is a noticeably higher variability in the LZa and LZb that significantly decreases in the MZ and particularly in the UZ (Table 12), attributable to plagioclase zoning and an elevated residual melt content in the lower part of the intrusion (Maaløe 1976a; Tegner et al. 2009; Humphreys 2009).

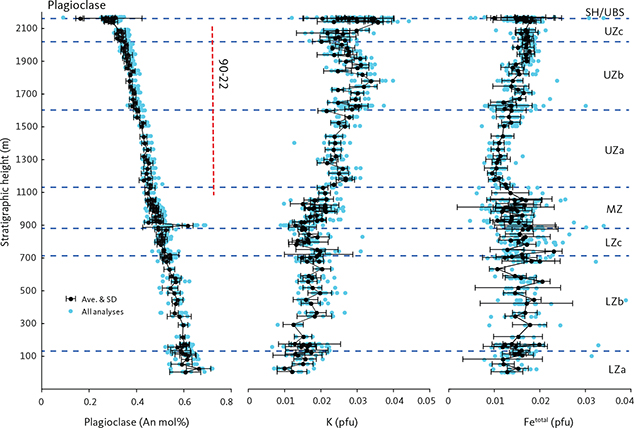
Fig. 26 Cryptic variation in plagioclase as a function of stratigraphic height (m) in the LS. Shown are anorthite content (An mol%) and the numbers of K and Fe^total cations pfu (8 oxygen). Iron is given as total Fe. Blue horizontal dashed lines: divisions of the LS. Symbols and abbreviations in Figs 2, 25.

The K content of plagioclase shows an irregular variation largely independent of the zone boundaries. The variation is irregular at around 0.015 pfu through LZ to the base of the MZ, then increases until the middle part of UZb, after which the content decreases into the UZc (Fig. 26). There is an apparent reversal to lower values in the lower part of UZa. The general increase in K in UZ was also observed by Jang & Naslund (2001), using bulk analyses of separated plagioclase. The Fe content on the other hand is within the range of 0.008 to 0.025 pfu in the LZ and MZ but increases from the base of UZa, all the way into the UZc, despite some irregularities. The UZ variation in Fe of plagioclase was interpreted as a corresponding enrichment in the liquid by Tegner (1997) and Tegner & Cawthorn (2010).

4.4.3 Pyroxenes

The clinopyroxene composition, expressed as mol% Mg/(Mg+Fe*) or Mg# (magnesium number), shows a systematic upward increase in iron from Mg# 71.6 ± 4.2 at the base of LZa to Mg# 0.8 ± 0.2 in UZc and at the SH (Table 12; Fig. 27). The Mg# in clinopyroxene decreases upward, accelerating slightly in LZc and even more so in UZb, and continues into UZc. The variation compares well to predicted ideal fractional crystallisation trends in a closed basaltic system (Maaløe 1976b; Morse 1996). The slope of the trend in Mg# varies from 1.3% per 100 m of stratigraphy in the LZ and UZa to 10% at the top of UZb. There are a few noticeable departures from the general upward increase in iron in the pyroxenes: at the base of UZa, again at the base of UZb, and for the UZc where Mg# rapidly levels off to zero. The reversal to higher Mg# at the base of UZb was also observed for olivine (Fig. 25).

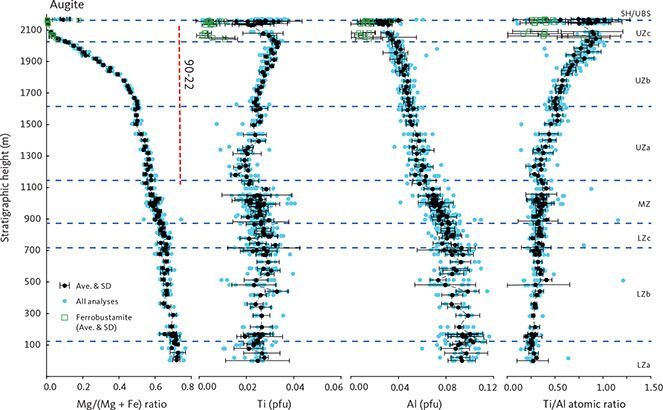
Fig. 27 Cryptic variation in pyroxenes (augite) as a function of stratigraphic height (m) in the LS (continued in Fig. 28). Shown are the atomic ratio Mg/(Mg + Fe), the numbers of Ti and Al cations pfu (4 cation and 6 oxygen) and the Ti/Al atomic ratio. Iron is given as total Fe. Green open squares: ferrobustamite. Blue horizontal dashed lines: divisions of the LS. Other symbols and abbreviations in Figs 2, 25.

The titanium content varies widely up to 0.005 pfu, although with an initially weak increase through LZa and LZb, followed by a decrease through LZc and the MZ, and terminated by a systematic increase from UZa to UZc (Fig. 27). The aluminium content appears to be relatively constant in LZa and LZb and then systematically decreases to UZc with few irregularities (except at the MZ–UZa boundary). Variable Ti and Al results in a systematic increase in the Ti/Al ratio with a break in slope at the MZ–UZa boundary corresponding to the variations in the non-quadrilateral components (Figs 19, 23). Both total Fe and Mn increase throughout, while Na shows some irregularities, but displays an overall up-section decrease, possibly interrupted by intervals showing constant or slightly increasing values (e.g. UZa; Fig. 27).

In addition to the variation in the main quadrilateral components, the early studies of the Skaergaard pyroxenes (Muir 1951; Brown et al. 1957; Brown & Vincent 1963) also observed strongly decreasing Al and constant Ti with fractionation for the clinopyroxene, corresponding to the variation observed in this study (Figs 27, 28). Nwe (1976) observed Mg# 71–73 for clinopyroxene in the lower part of the Cambridge Drill Core, which is within the maximum range observed (Table 5). Clinopyroxene in the MBS reaches Mg# 74–79 (Thy et al. 2008; Humphreys & Holness 2010; Namur et al. 2013).

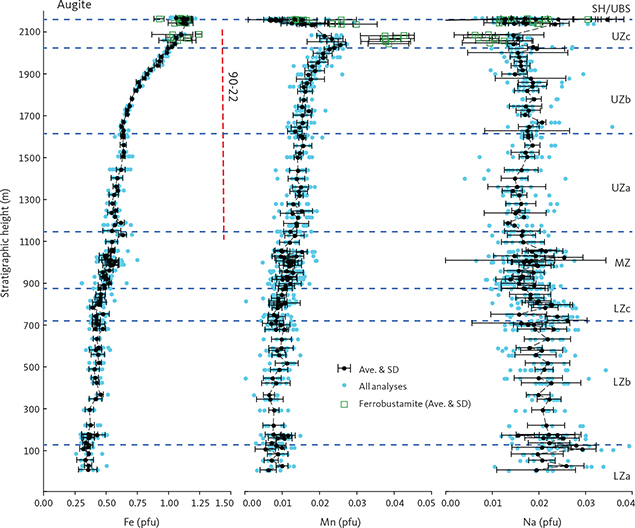
Fig. 28 Cryptic variation in pyroxenes (augite) as a function of stratigraphic height (m) in the LS (continued from Fig. 27). Shown are the numbers of Fe, Mn and Na cations pfu (4 cation and 6 oxygen). Iron is given as total Fe. Green open squares: ferrobustamite. Blue horizontal dashed lines: divisions of the LS. Other symbols and abbreviations in Figs 2, 25.

The orthopyroxene composition matches that for olivine and clinopyroxene with a generally systematic upward increase in iron from Mg# 71.6 ± 4.2 at the base of LZa to 0.2 ± 0.3 at the top of the UZc and the SH (Table 12). The inverted ferrobustamite shows limited variation reflecting their stratigraphically narrow occurrence in the UZc.

4.4.4 FeTi oxides

Both ilmenite and magnetite were analysed with a broad electron beam to obtain coexisting reconstituted mineral compositions approaching liquidus conditions. The success of this approach can be evaluated using the partitioning of Mn and Mg between the coexisting phases. Bacon & Hirschmann (1988) argued that the exchange coefficient calculated as K_D = (Mg/Mn)^mt / (Mg/Mn)^il for liquidus conditions (Il: ilmenite; Mt: magnitite) were largely independent of temperature and composition and thus constant at 0.93. The K_D (Mg/Mn) for this study varies widely at an average of 0.79 ± 0.40 with no systematic stratigraphic variations and encompasses the value for ideal liquidus conditions. The large standard deviation observed suggests limited success in obtaining liquidus oxide compositions, although it is possible that low-temperature, oxidation-exsolution of magnetite (Buddington & Lindsley 1964) may selectively affect Mg and Mn partitioning (Bacon & Hirschmann 1988).

Both ilmenite and magnetite show systematic upward decreases in magnesium from their appearances as primocrysts in LZc (Fig. 29). Despite large variations, other variables such as hematite in ilmenite show a systematic decrease from LZc into UZa. Ulvöspinel in magnetite also shows large variation but appears relatively constant until the upper part of UZb, where high oxidation can be observed. In the LZa to LZb, where the FeTi oxides are late-crystallising phases, there is little systematic compositional variation, except for a systematic increase for ulvöspinel for magnetite through LZb.

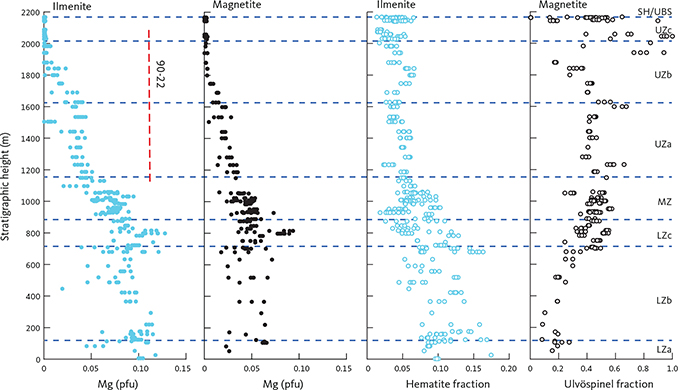
Fig. 29 Cryptic variation in ilmenite (blue) and magnetite (black) as a function of stratigraphic height (m) in the LS. Shown are the numbers of Mg cations pfu (ilmenite calculated as 2 cations and 3 oxygens and magnetite as 3 cations and 4 oxygens) as individual point analyses. Shown are numbers of Mg cations pfu in ilmenite and magnetite, mole fractions of hematite in ilmenite, and mole fraction of ulvöspinel in magnetite. Compare to Fig. 24 and Table 9. Red vertical dashed line: location of drill core 90-22. Blue horizontal dashed lines: divisions of the LS. Abbreviations in Figs 2, 25.

4.4.5 Relative cryptic changes

Figures 25–29 show that the most dramatic changes in primocryst compositions are found in the UZ. The relative changes in the composition of plagioclase, olivine and augite across the UZ are shown in Fig. 30 in terms of An content, Fo content and pyroxene Mg/(Mg+Fe^total) ratio. We refer to this as derivative cryptic variation that steadily increases up through UZa and into UZb, reaching a maximum at 1962 m. Above this, the changes reduce and eventually reach a constant value at the UZb–UZc boundary. All three silicates show parallel variation with the lowest values for plagioclase, then olivine and highest for clinopyroxene. A slight increase resumes from the base of the UZc, reaching a maximum in the centre of the UZc, and subsequently decreases until the SH. The UZc variation resembles the symmetric pattern of a sill-like segregation cap cooled both from the base and from the top.

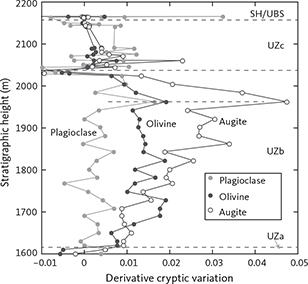
Fig. 30 Derivative cryptic variation in the UZb and UZc for coexisting olivine (as Fo mol%), plagioclase (as An mol%) and augite (as Mg/(Mg+Fe^total) atomic ratio). Averages are calculated as fractions in steps of four consecutive determinations.

4.4.6 Co-variation of silicate minerals

The composition of mafic silicate minerals is shown in Fig. 31 as a function of coexisting plagioclase primocrysts. For similar An contents, the Mg/(Mg+Fe^total) ratio is highest for clinopyroxene, followed by orthopyroxene and finally lowest for olivine. Mafic minerals are shown in Fig. 32 as a function of clinopyroxene composition, where forsterite of olivine defines a polynomial curve, between zero and c. 70% Mg#. Orthopyroxene with higher Mg# shows an apparent linear relationship only reaching values of just below 50% Mg#.

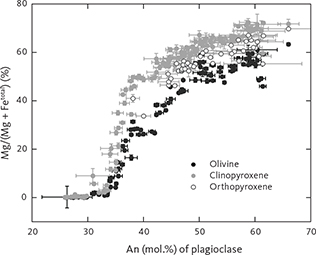
Fig. 31 Mg/(Mg + Fe^total) content in coexisting mafic minerals (olivine, clinopyroxene, and orthopyroxenes; %) vs. An (mol%) of coexisting plagioclase. The horizontal and vertical bars are the 1σ SD of repeated analyses in individual thin sections.

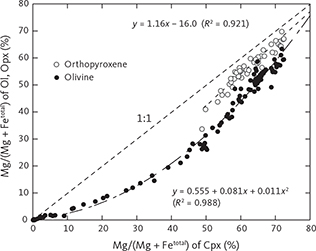
Fig. 32 Mg/(Mg + Fe^total) content in coexisting olivine (Ol) and orthopyroxene (Opx; %) vs. Mg/(Mg + Fe^total) content in coexisting clinopyroxenes (Cpx; %). Equations for the best fits to olivine and orthopyroxene are given.

4.5 Bulk-rock compositions

The composition of the gabbros is principally controlled by modal proportions of primocrysts formed onto the solid substrata or walls of the chamber. Although the individual phase compositions may reflect the coexisting melt composition, or equilibrium, their relative proportions reflect selective accumulation and redistribution processes operating during the early stages of gabbro formation. The spectacular and complex layering preserved throughout the intrusion reflects such processes, although their detailed explanations have been debated (Wager & Brown 1967; Irvine 1979; Maaløe 1978; Hunter 1987; Namur et al. 2015).

It is likely that the melt component of the crystal mush, which was originally formed and trapped on the magma floor, may have been either retained or migrated upwards into the overlaying mush. Here it may have crystallised, altering interstitial melt composition and possibly reacting with the solid components, and thus complicating the understanding of gabbro compositions. Despite the possibility for such late-stage modification, the overall composition of the gabbros will mainly record the proportions of primocryst in addition to a lesser amount of trapped melt mostly crystallised as the same minerals and in the same proportions.

Major elements are in the following sections defined as elements that are essential for forming the main primocrysts, while trace elements are defined as elements not essential to building the structure of the primocrysts, with some exceptions as we show in the following sections. The trace elements are discussed as two different groups, either included in the silicate building blocks or excluded from them and residing in the melt.

4.5.1 Major elements

This section will only describe the stratigraphic changes in the gabbro compositions that can be related to the principal changes in primocryst assemblages for the individual zone and subzone divisions. The major element composition of the gabbros is illustrated in Fig. 33 and summarised in Table 13. The average zone compositions for the composite profile are shown in Table 14 and compare remarkably well to similar lateral intrusion-wide estimates by McBirney (1989a).

Table 13 Summary of gabbro major element compositions

Zone	Stratigraphic height (m)		F	SiO2 (wt%)		TiO2 (wt%)		Al2O3 (wt%)		Fe2O3 (wt%)		FeO (wt%)		MnO (wt%)		MgO (wt%)		CaO (wt%)		Na2O (wt%)		K2O (wt%)		P2O5 (wt%)		Total (wt%)
	high	low		Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD
UBS	2169	2165		51.82	2.380	1.97	0.530	10.43	1.161	5.48	2.272	15.28	3.298	0.26	0.080	0.72	0.632	7.08	0.770	3.61	0.486	0.98	0.099	0.61	0.318	98.23
UZc	2165	2165	0.000	50.17	3.477	1.87	0.492	9.40	2.397	6.28	0.844	18.45	4.759	0.19	0.011	0.03	0.016	7.89	1.063	3.25	0.948	0.80	0.156	0.36	0.202	98.70
UZc	2165	2164	0.000	47.37	1.453	2.69	0.918	7.28	0.642	7.02	1.094	20.88	1.869	0.25	0.026	0.02	0.005	8.71	0.645	2.52	0.210	0.77	0.095	0.67	0.140	98.19
UZc	2163	2147	0.001	48.11	2.422	2.46	0.505	7.83	1.729	6.21	1.924	20.61	1.172	0.32	0.129	0.03	0.023	8.55	0.453	2.69	0.612	0.68	0.100	0.63	0.214	98.11
UZc	2144	2141	0.003	45.77	2.241	2.57	0.153	6.64	0.871	5.18	1.503	24.82	3.120	0.48	0.078	0.07	0.015	9.36	0.906	2.24	0.453	0.56	0.190	0.75	0.105	98.44
UZc	2091	2081	0.010	45.15	0.652	2.70	0.244	8.32	0.429	2.88	0.323	24.73	0.655	0.72	0.013	0.26	0.040	10.38	0.316	2.52	0.130	0.26	0.033	0.78	0.040	98.71
UZc	2075	2060	0.012	44.51	0.484	2.78	0.173	7.43	0.387	3.09	0.647	26.13	1.540	0.84	0.054	0.36	0.084	10.26	0.060	2.32	0.138	0.27	0.037	0.87	0.071	98.85
UZc	2060	2046	0.014	45.64	0.914	2.54	0.262	8.98	1.391	2.68	0.311	23.96	1.852	0.74	0.244	0.68	0.332	9.65	0.427	2.68	0.359	0.32	0.033	0.71	0.067	98.57
UZb	2044	2030	0.016	51.69	8.596	2.02	0.618	9.15	0.200	4.77	1.651	18.23	7.241	0.49	0.190	0.39	0.402	7.31	2.858	3.35	0.774	0.53	0.247	0.53	0.216	98.46
UZb	2024	1984	0.019	44.75	1.783	2.83	0.372	10.00	0.322	4.17	0.733	22.21	1.147	0.46	0.017	1.37	0.277	9.40	0.279	2.89	0.139	0.31	0.046	0.90	0.296	99.29
UZb	1962	1921	0.029	44.06	0.737	3.01	0.129	10.83	0.342	4.27	0.854	20.88	0.422	0.42	0.007	1.95	0.234	9.13	0.359	3.01	0.122	0.32	0.033	1.18	0.064	99.05
UZb	1902	1862	0.039	44.10	0.664	3.29	0.110	12.14	0.254	3.73	0.435	19.11	0.790	0.35	0.007	2.35	0.192	8.88	0.068	3.30	0.093	0.35	0.040	1.46	0.093	99.06
UZb	1843	1801	0.050	41.69	1.855	3.91	0.343	10.82	1.501	3.71	0.743	20.90	2.232	0.35	0.039	3.46	0.616	9.18	0.051	2.89	0.437	0.27	0.061	1.87	0.158	99.04
UZb	1782	1748	0.062	41.26	0.613	4.15	0.110	10.38	0.066	2.79	0.109	21.40	0.386	0.33	0.007	4.14	0.271	9.40	0.213	2.75	0.016	0.35	0.117	2.06	0.301	99.02
UZb	1728	1691	0.073	37.73	1.926	5.24	1.058	10.13	0.142	3.37	0.379	22.21	0.670	0.33	0.011	4.53	0.405	9.56	0.609	2.61	0.022	0.21	0.021	3.12	0.832	99.03
UZb	1671	1630	0.086	40.77	2.844	4.34	1.165	10.80	1.178	3.19	0.947	18.41	2.369	0.29	0.028	4.86	0.590	10.60	0.636	2.79	0.344	0.23	0.044	2.84	0.061	99.13
UZb	1620	1600	0.097	42.36	3.153	4.79	0.335	10.74	1.158	4.70	0.755	16.97	2.009	0.27	0.027	4.80	0.464	10.36	1.043	2.66	0.302	0.22	0.052	1.27	1.939	99.13
UZa	1561	1527	0.112	45.93	0.538	4.66	0.374	13.28	0.488	3.20	1.264	15.06	1.499	0.25	0.021	4.43	0.399	8.93	0.400	3.21	0.129	0.24	0.042	0.06	0.017	99.25
UZa	1506	1431	0.126	45.30	1.778	5.28	0.904	12.55	1.294	3.52	0.880	14.54	2.714	0.26	0.032	5.09	1.101	9.41	0.465	2.96	0.385	0.25	0.119	0.04	0.009	99.20
UZa	1403	1343	0.154	45.38	3.099	4.94	2.220	13.04	1.158	3.21	0.987	14.55	1.681	0.24	0.019	5.32	0.186	9.50	0.557	2.93	0.238	0.20	0.014	0.05	0.000	99.38
UZa	1323	1282	0.177	43.93	0.519	5.55	0.249	11.97	0.113	3.85	0.037	15.53	0.558	0.26	0.000	6.12	0.134	9.36	0.287	2.63	0.026	0.16	0.000	0.05	0.000	99.41
UZa	1268	1237	0.194	44.28	4.507	5.11	1.999	11.99	0.955	4.65	1.745	14.46	2.973	0.25	0.017	5.81	0.215	9.89	1.007	2.60	0.277	0.17	0.049	0.06	0.044	99.29
UZa	1218	1188	0.210	45.52	1.463	5.58	0.439	12.01	0.563	3.44	1.142	13.78	0.840	0.25	0.009	5.95	0.300	10.12	0.668	2.64	0.135	0.20	0.014	0.08	0.000	99.55
UZa	1178	1131	0.224	44.14	0.649	5.79	0.589	11.91	0.632	4.88	1.468	13.79	0.485	0.25	0.009	5.96	0.250	9.79	0.314	2.53	0.115	0.18	0.014	0.06	0.011	99.27
MZ	1098	1055	0.251	42.53	3.036	7.86	1.588	13.54	3.932	4.32	1.104	13.81	3.621	0.22	0.060	4.88	1.802	9.16	0.166	2.80	0.858	0.17	0.050	0.05	0.013	99.35
MZ	1053	1032	0.267	41.65	4.135	9.97	3.828	9.76	0.934	2.65	3.955	15.60	1.718	0.28	0.007	7.20	0.149	10.21	0.836	1.96	0.220	0.11	0.029	0.03	0.016	99.41
MZ	1024	1009	0.277	43.31	3.194	6.11	2.330	11.12	0.149	3.98	0.922	15.00	1.352	0.26	0.000	7.09	0.714	10.20	0.592	2.18	0.050	0.13	0.018	0.04	0.014	99.43
MZ	1003	1002	0.285	41.10	6.235	7.91	3.671	12.69	3.992	4.88	2.175	14.83	4.681	0.23	0.061	5.33	1.465	9.78	1.151	2.45	0.850	0.14	0.053	0.04	0.016	99.38
MZ	988	961	0.291	39.13	4.190	9.87	3.100	8.45	2.078	5.21	1.489	17.01	1.541	0.29	0.027	7.72	1.593	10.02	1.799	1.58	0.404	0.10	0.017	0.03	0.005	99.42
MZ	953	930	0.304	38.12	4.573	9.71	1.935	11.43	1.436	5.88	2.111	16.30	3.138	0.24	0.022	5.75	0.599	9.47	1.072	2.10	0.344	0.12	0.028	0.03	0.015	99.14
MZ	921	900	0.316	44.10	5.155	5.89	3.728	14.58	3.579	2.96	2.140	12.48	3.980	0.19	0.046	5.73	0.477	10.77	1.064	2.55	0.446	0.13	0.039	0.02	0.013	99.41
MZ	890	875	0.329	39.63	2.472	9.05	1.346	12.80	1.361	5.62	1.023	14.26	1.436	0.21	0.021	5.57	0.860	9.79	0.834	2.30	0.270	0.11	0.022	0.02	0.006	99.37
LZc	847	816	0.346	34.13	8.867	12.35	5.331	9.67	2.968	6.76	2.906	18.74	5.849	0.26	0.042	6.68	0.508	8.68	2.075	1.68	0.600	0.09	0.034	0.02	0.009	99.06
LZc	808	798	0.362	29.49	11.200	15.31	6.993	9.42	3.224	9.07	4.277	20.38	6.279	0.26	0.046	5.87	0.535	7.20	2.732	1.58	0.687	0.09	0.045	0.02	0.013	98.70
LZc	784	742	0.372	44.66	6.660	5.07	4.875	10.45	4.329	3.92	1.929	12.52	2.908	0.22	0.040	8.37	3.315	12.09	3.062	1.86	0.776	0.13	0.044	0.05	0.025	99.34
LZc	723	703	0.398	48.70	2.274	1.61	0.973	13.98	1.591	2.01	1.554	10.01	2.553	0.19	0.034	8.28	2.303	11.73	1.429	2.46	0.269	0.18	0.003	0.06	0.013	99.19
LZb	703	681	0.406	48.76	1.737	1.73	0.650	15.60	2.312	1.77	1.171	9.89	1.914	0.17	0.028	7.50	2.049	11.19	0.104	2.73	0.490	0.18	0.047	0.05	0.024	99.57
LZb	634	580	0.437	50.46	0.819	1.32	0.035	15.45	3.382	1.27	0.369	8.44	1.965	0.17	0.035	7.13	2.144	12.32	1.327	2.64	0.608	0.20	0.054	0.08	0.022	99.49
LZb	558	488	0.472	49.03	1.682	1.31	0.151	14.83	1.829	1.71	0.539	9.77	2.619	0.18	0.037	8.64	2.205	11.21	1.474	2.45	0.306	0.18	0.031	0.08	0.027	99.39
LZb	447	367	0.526	49.28	2.157	1.27	0.088	16.02	2.696	1.65	0.275	9.50	3.866	0.17	0.048	7.81	3.006	10.99	1.295	2.65	0.477	0.22	0.055	0.10	0.033	99.65
LZb	346	221	0.576	48.22	2.536	1.10	0.326	14.72	3.996	1.21	0.307	10.72	5.528	0.18	0.070	10.05	3.535	11.03	1.854	2.26	0.545	0.18	0.062	0.07	0.036	99.73
LZb	177	173	0.667	49.46	1.199	1.33	0.317	18.17	4.365	1.53	0.127	7.79	2.964	0.14	0.048	6.93	3.043	11.33	1.035	2.79	0.588	0.25	0.030	0.11	0.006	99.84
LZa	161	137	0.676	48.60	0.432	1.30	0.169	17.62	0.521	1.63	0.375	8.88	0.386	0.16	0.007	8.10	0.588	10.31	0.562	2.70	0.084	0.26	0.025	0.12	0.016	99.67
LZa	125	107	0.696	47.38	1.239	1.53	0.318	15.90	2.174	1.43	0.463	11.08	1.924	0.18	0.032	9.98	1.916	9.16	0.885	2.46	0.278	0.26	0.021	0.14	0.017	99.49
LZa	96	27	0.712	48.75	0.561	1.42	0.019	18.69	1.537	1.35	0.191	8.40	0.846	0.15	0.015	7.02	1.739	10.84	0.520	2.73	0.177	0.26	0.010	0.13	0.015	99.75
LZa	7		0.764	48.16		1.36		16.91		0.58		10.09		0.16		9.01		10.52		2.41		0.24		0.13		99.58
Calculated as averages (Ave.) of three consecutive samples with 1σ SD calculated for n > 2. F: melt remaining after Tegner et al. (2009), (Eq.) 1. Stratigraphic height is given as high and low referring to the interval used for averaging. Complete data set in Supplementary File S1.

 

Table 14 Average zone and subzone major and trace element compositions

Zone	UZc		UZb		UZa		MZ		LZc		LZb		LZa
n	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD
	21		24		21		25		12		19		12
	Major element concentrations (wt%)
SiO2	46.67	2.49	42.73	4.21	44.88	2.09	41.78	4.08	37.46	9.49	49.11	1.73	48.23	1.35
TiO2	2.52	0.49	3.71	1.06	5.18	1.07	7.79	2.80	9.91	6.43	1.41	0.46	1.35	0.23
Al2O3	7.98	1.44	10.57	0.97	12.28	1.03	11.81	2.87	10.56	3.01	15.30	2.27	17.54	2.58
Fe2O3	4.76	1.97	3.71	0.84	3.92	1.23	4.43	1.84	6.13	3.30	1.58	0.74	1.34	0.41
FeO	22.80	3.39	20.42	2.42	14.78	1.77	14.74	2.87	16.42	5.18	9.56	2.74	9.38	2.30
FeO*	27.55	2.71	24.12	5.29	18.69	2.29	19.16	5.54	22.54	8.08	11.13	2.86	10.72	2.31
MnO	0.51	0.27	0.37	0.08	0.26	0.02	0.24	0.04	0.24	0.04	0.17	0.04	0.16	0.03
MgO	0.21	0.26	3.08	1.54	5.41	0.75	6.17	1.32	7.02	2.24	8.14	2.24	8.50	2.81
CaO	9.26	1.02	9.36	1.13	9.56	0.60	9.95	0.98	9.41	2.71	11.44	1.23	10.13	1.07
Na2O	2.60	0.52	2.92	0.34	2.80	0.31	2.28	0.57	1.85	0.59	2.54	0.40	2.62	0.38
K2O	0.52	0.24	0.31	0.11	0.21	0.06	0.13	0.04	0.11	0.04	0.20	0.04	0.25	0.02
P2O5	0.68	0.19	1.87	0.94	0.07	0.04	0.04	0.01	0.03	0.02	0.08	0.03	0.13	0.02
LOI	1.20	0.39					0.60	0.12	0.55	0.17	0.70	0.08	0.70	0.14
Total	99.71		99.03		99.33		99.96		99.68		100.23		100.34
	Selected average trace element concentrations (ppm)
Sc	37		49		47		54		52		36		24
V	36		36		374		982		1410		346		227
Cr	11		8		8		10		71		197		79
Co	2.6		4		16		59		122		126		192
Ni	13		78		91		82		89		54		59
Cu	296		835		995		128		86		94		138
Zn	224		144		109		96		95		78		83
Rb	12		3.9		2.2		1.1		1.3		2.6		4.3
Sr	400		282		285		226		198		277		298
Y	136		40		13		8		8.54		13		17
Zr	216		62		53		47		49		53		69
Nb	50		9		8		9		7		4.6		8
Ba	238		75		57		32		30		50		63
Hf	5		1.7		1.5		1.3		1.4		1.5		1.9
Ta	2.9		0.83		0.84		0.77		0.55		0.3		0.53
Pb	2.6		1.1		0.63		0.91		0.90		1.1		1.3
Th	1.5		0.51		0.22		0.10		0.13		0.33		0.56
U	0.40		0.15		0.07		0.03		0.04		0.09		0.16
La	28		13		3.3		1.8		2.1		4.3		7
Yb	1.7		0.35		0.17		0.13		0.12		0.17		0.20
	LS estimates by McBirney (1989a)
SiO2	45.13		41.17		42.62		42.43		40.73		48.39		47.88
TiO2	2.58		4.01		5.61		6.73		6.85		1.43		1.48
Al2O3	7.71		9.37		11.05		11.43		10.92		12.43		16.65
Fe2O3	5.69		5.63		4.98		6.07		6.63		2.56		2.35
FeO	23.00		21.19		17.80		14.37		14.95		10.42		9.35
FeO*	28.12		26.26		22.28		19.83		20.92		12.72		11.46
MnO	0.64		0.41		0.30		0.26		0.26		0.21		0.17
MgO	0.38		3.36		5.56		6.19		6.19		10.04		8.78
CaO	9.95		9.23		8.53		9.79		9.68		11.46		10.08
Na2O	2.38		2.55		2.52		2.21		1.96		2.11		2.54
K2O	0.40		0.35		0.26		0.21		0.16		0.20		0.27
P2O5	0.83		1.85		0.21		0.08		0.04		0.09		0.11
LOI	1.12		0.77		0.64		0.50		0.26		0.56		0.54
Total	99.81		99.89		100.08		100.27		98.63		99.90		100.20
n: number of analyses used for each average (Ave.) and 1σ SD for n > 2. LOI: loss on ignitation at 950°C (not determined for UZb and UZa) FeO*: total iron as FeO. LS: Layered Series.

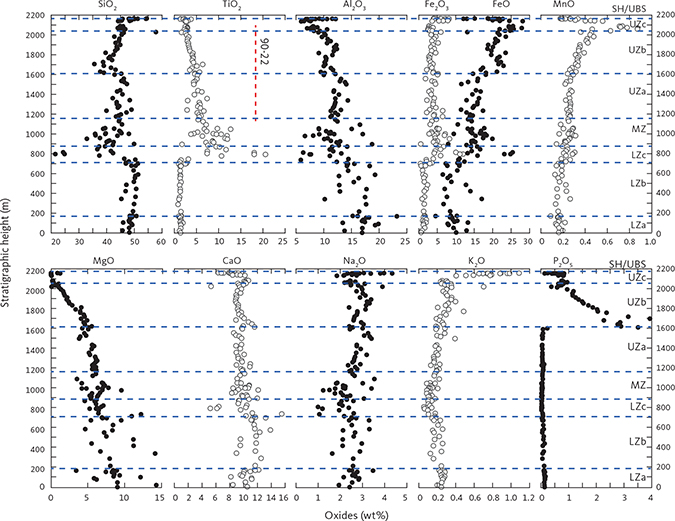
Fig. 33 Major elements of the LS gabbros, shown as oxides (wt%) vs. stratigraphic height (m). Blue horizontal dashed lines: divisions of the LS. Abbreviations in Fig. 2. Red vertical dashed line: location of drill core 90-22.

The volatile component expressed as LOI was only determined for the surface samples (n = 86) for which the average is 0.64 ± 0.14% in the LZ and MZ and rising to 1.22 ± 0.38% in the UZc (not shown). The Fe₂O₃/FeO ratio (also not shown) is relatively constant throughout LZa and LZb at 0.17 ± 0.07, then increases markedly in LZc to 0.35 ± 0.10, after which the ratio steadily decreases to 0.12 ± 0.02 in the lower part of UZc, and increases to 0.33 ± 0.12 in the upper part of the UZc and SH. This variation closely mimics the appearance of magnetite and its modal decrease upward and suggests only a modest secondary oxidation for the majority of the profile. The exception is the upper part of the UZc, which may indicate some late-stage or secondary oxidation.

The variation of many of the major elements clearly shows the onset of FeTi oxides as a primocryst at the LZb–LZc boundary (Fig. 33). This is as expected, particularly where TiO₂ abruptly increases, Fe₂O₃, FeO increases and SiO₂ decreases. The modal composition suggests that ilmenite is the dominating FeTi oxide, and that magnetite occurs in lower proportions than ilmenite (Fig. 15).

The transition from LZa to LZb is weakly defined by a lower CaO content in the former, which corresponds to the observed lower modal content of clinopyroxene in LZa (Fig. 15) and supports the traditional definition of the LZa as lacking clinopyroxene as a primocryst (Wager & Brown 1967).

The appearance of apatite as a primocryst at the UZa–UZb boundary is likewise strongly reflected in the P₂O₅ content, which is low below the boundary, often just above the detection limit, but abruptly increases to nearly 4 wt% at the base of UZb. Concurrent with the increase in P₂O₅ is a smaller rise in CaO that can also be understood in terms of apatite accumulation. Manganese shows a weak rise through UZb and followed by a marked rise in UZc that can be correlated to the appearance of inverted ferrobustamite in this subzone (Fig. 20). The gabbro fluorine content is closely positively correlated with the modal amount of apatite (see Supplementary File S1).

The transition from UZa to UZb, where SiO₂ and Al₂O₃ drop and FeO and CaO rise, cannot directly be related to the appearance of primocryst apatite, even at the maximum amount of 10%. They can, however, be related to the high amounts of both iron-rich olivine and apatite observed at the base of the UZb as shown by the olivine and apatite modes (Fig. 14; see also Sections 5.7.7 and 5.11.8 on the effects of liquid immiscibility). The MZ also shows large variations, but these cannot univocally be related to the reaction of olivine with interstitial melt to form orthopyroxene as suggested by the petrography (Fig. 9). Other large variations can be attributed to heterogeneity due to modal layering, particularly in the LZc. Such variation highlights the problems associated with sampling highly heterogeneous rocks, such as layered gabbros. However, these consistent trends attest to some success with the sampling of the average modal compositions.

4.5.2 Trace elements

Trace element concentrations in the gabbros (Figs 34, 35; summarised in Tables 15, 16) vary, like the major elements, with mineral assembly, mineral modes and differentiation as a function of stratigraphic position.

Table 15 Summary of gabbro trace element compositions

Zone	Stratigraphic height (m)		Sc (ppm)		V (ppm)		Cr (ppm)		Ni (ppm)		Co (ppm)		Cu (ppm)		Zn (ppm)		Rb (ppm)		Sr (ppm)		Y (ppm)		Zr (ppm)		Nb (ppm)		Ba (ppm)		Hf (ppm)		W (ppm)		Ta (ppm)		Pb (ppm)		Th (ppm)		U (ppm)
	high	low	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD
UBS	2169	2165	31	3	25	1	22	3	3.6	1.3	15	11	143	155	248	54	21	2	474	115	157	32	302	12	93	44	407	48	8	0.31	0.42	0.03	6	2.170	4.4	0.3	2.5	0.3	0.64	0.06
UZc	2165	2165	44		24		22		3.7		3.4		72	1	259		16		570		117		398		52		349		9		0.31		3.0		3.4		2.1		0.56
UZc	2165	2164	45	6	49	22	8	10	2.5	0.3	2.5	0.7	112	19	317	7	15	2	457	45	219	26	246	17	105	28	318	20	7	0.36	0.31	0.02	6	1.057	3.5	0.1	1.9	0.4	0.51	0.10
UZc	2163	2147	39	5	61	0	2.2	1.6	3.1	0.9	2.6	1.4	142	64	232	20	12	3	419	126	154	38	318	183	52	18	273	69	7	2.82	0.24	0.04	2.8	1.062	2.8	0.5	1.7	0.4	0.45	0.07
UZc	2144	2141	37		61		3.1		3.5		4.9		184	71	196		9		323		145		127		28		162		3.4		0.19		1.6		2.0		1.1		0.31
UZc	2091	2081	30	2	24	32	6	5	1.5	1.1	34	22	679	95	156	16	3.8	1.5	300	26	77	11	52	8	9	1	78	10	1.4	0.1			0.83	0.177	0.92	0.30	0.50	0.07	0.14	0.02
UZc	2075	2060	30	1	6	2	10	2	0.64	0.55	29	21	744	128	158	14	4.2	1.2	258	32	85	8	71	15	11	0	79	5	1.9	0.3			0.93	0.127	0.78	0.11	0.59	0.07	0.18	0.00
UZc	2060	2046	37	19	6	2	10	4	0.90	1.01	37	14	640	169	153	15	4.6	0.7	298	75	62	24	77	4	11	1	87	5	2.0	0.1			0.85	0.199	1.0	0.1	0.66	0.15	0.19	0.03
UZb	2044	2030	49		5		8		0.23		51		360	56	159		6		284		50		91		13		99		2.5				1.1		1.9		0.82		0.21
UZb	2024	1984	73	5			9	0	5	0	54	1	668	184	174	12	4.6	0.9	319	28	35	1	49	7	8	0	83	17	1.5	0.1			0.75	0.04	1.1	0.2	0.50	0.09	0.12	0.00
UZb	1962	1921	63	4			9	0	4.4	0.0	59	1	836	108	151	4	4.6	1.4	296	23	32	1	50	7	7	0	77	2	1.5	0.2			0.65	0.04	1.1	0.1	0.47	0.01	0.13	0.00
UZb	1902	1862	52	2	1.0	0.5	9	0	4.4	0.1	64	8	779	24	138	5	4.9	1.3	297	2	32	1	60	2	8	1	82	7	1.6	0.1			0.67	0.04	1.0	0.1	0.52	0.04	0.15	0.01
UZb	1843	1801	49	8	16	1	9	0	3.5	0.1	75	10	861	136	130	13	3.6	1.5	259	40	39	6	59	7	8	2	68	12	1.6	0.2			0.76	0.15	1.1	0.3	0.50	0.15	0.17	0.03
UZb	1782	1748	42	2	22	3	9	0	3.6	0.1	97	7	786	62	138	1	3.9	0.1	263	1	43	4	71	4	9	1	73	2	1.9	0.1			0.96	0.11	0.90	0.05	0.52	0.04	0.17	0.01
UZb	1728	1691	30	3	37	10	9	0	5	1	100	13	1251	287	137	2	2.5	0.5	268	9	53	10	59	6	10	2	61	6	1.6	0.1			1.0	0.2	0.71	0.11	0.43	0.05	0.16	0.02
UZb	1671	1630	34	2	44	13	6	0	4.4	0.4	98	15	970	64	125	11	2.7	0.8	283	30	49	2	60	1	9	1	69	12	1.6	0.1			0.87	0.10	0.93	0.37	0.44	0.07	0.16	0.02
UZb	1620	1600	46	12	124	32	6	0	6	0	103	5	1008	447	144	20	2.5	0.9	267	25	31	22	57	7	7	1	63	13	1.6	0.2			0.67	0.08	0.79	0.17	0.35	0.08	0.12	0.04
UZa	1561	1527	44	0	103	34	6	0	6	0	87	3	797	351	116	7	2.4	0.7	322	12	12	2	51	11	10	4	71	10	1.4	0.3			0.92	0.33	0.72	0.16	0.21	0.07	0.071	0.016
UZa	1506	1431	49	3	160	32	9	0	11	1	87	12	1048	185	109	1	3.5	3.3	304	33	12	3	52	8	9	2	63	19	1.4	0.2			0.92	0.17	0.56	0.21	0.20	0.10	0.052	0.021
UZa	1403	1343	47	3	270	72	9	0	12	0	89	8	928	61	107	11	1.9	0.1	301	24	12	0	49	9	7	3	55	5	1.4	0.2			0.76	0.28	0.53	0.02	0.20	0.02	0.058	0.004
UZa	1323	1282	47	1	406	14	9	0	18	1	104	13	699	400	111	3	1.6	0.2	265	7	11	1	48	3	8	1	47	3	1.3	0.1			0.87	0.07	0.47	0.03	0.19	0.02	0.057	0.010
UZa	1268	1237	47	2	571	308	8	0	21	5	95	14	1419	490	114	23	1.6	0.8	261	24	13	5	49	11	7	2	51	12	1.3	0.3			0.69	0.15	0.79	0.60	0.23	0.17	0.073	0.029
UZa	1218	1188	49	4	484	137	8	0	21	3	90	9	602	345	103	10	2.5	0.2	263	16	17	1	68	2	10	0	57	4	1.8	0.1			0.91	0.04	0.61	0.05	0.31	0.03	0.091	0.006
UZa	1178	1131	44	8	623	177	7	2	24	4	81	29	1474	689	105	19	2.1	0.4	279	46	12	5	57	8	9	2	54	4	1.5	0.2			0.79	0.07	0.71	0.26	0.23	0.06	0.069	0.018
MZ	1098	1055	50	11	747	170	4.2	0.3	31	6	79	13	384	459	101	5	1.6	0.0	250	66	9	2	51	6	10	2	41	8	1.4	0.2	0.15	0.09	0.77	0.23	0.99	0.04	0.15	0.01	0.043	0.004
MZ	1053	1032	64		599		5		33		78		74	36	89		0.89		191		9		54		14		27		1.5		0.085		1.2		0.87		0.075		0.024
MZ	1024	1009	56	3	892	216	4.4	0.4	53	7	85	9	103	3	99	5	1.3	0.4	220	7	10	3	44	1	7	2	34	5	1.2	0.0	0.089	0.007	0.57	0.16	0.95	0.07	0.13	0.05	0.037	0.014
MZ	1003	1002	51	13	1084	454	6	3	49	16	84	29	108	11	101	16	1.1	0.5	253	96	8	3	48	7	9	3	37	14	1.3	0.2	0.094	0.003	0.70	0.31	0.94	0.10	0.12	0.06	0.032	0.012
MZ	988	961	65	12	1091	254	4.3	1.0	70	10	98	11	109	23	103	8	1.1	0.2	151	49	12	6	60	6	12	3	25	4	1.7	0.2	0.090	0.002	0.99	0.28	0.92	0.06	0.11	0.04	0.033	0.010
MZ	953	930	52		1190		5		72		82		107	6	96		1.2		228		8		48		9		33		1.3		0.091		0.77		0.89		0.11		0.033
MZ	921	900	45	10	846	528	42	61	73	14	68	25	57	28	87	14	0.82	0.47	273	65	5	1	33	9	6	2	33	11	1.0	0.2	0.089	0.005	0.48	0.23	0.86	0.11	0.060	0.056	0.019	0.014
MZ	890	875	48	5	1409	241	7	2	95	18	84	11	78	17	95	7	0.86	0.40	241	30	5	1	40	5	8	1	29	5	1.2	0.1	0.087	0.005	0.71	0.11	0.86	0.05	0.058	0.024	0.019	0.010
LZc	847	816	53		1373		6		99		93		95	20	96		0.89		207		6		48		8		26		1.4		1.3		0.65		0.87		0.086		0.026
LZc	808	798	51	1	2314	1029	22	10	163	56	134	49	96	11	116	24	0.73	0.49	155	81	3.1	3.6	56	9	11	4	20	12	1.6	0.3	0.087	0.002	0.93	0.36	0.84	0.08	0.067	0.054	0.024	0.012
LZc	784	742	60	21	1352	699	105	103	110	13	73	17	81	9	90	11	1.4	0.7	181	87	13	9	50	10	5	3	31	10	1.5	0.3	0.486	0.681	0.39	0.30	0.88	0.10	0.16	0.12	0.047	0.032
LZc	723	703	44	4	601	480	151	72	115	50	59	23	71	14	79	13	2.2	0.6	248	28	12	1	41	8	3.3	0.9	43	2	1.2	0.2	0.870	0.679	0.22	0.05	1.0	0.0	0.22	0.09	0.057	0.016
LZb	703	681	38	6	608	402	393	318	113	38	58	14	79	18	79	7	1.7	0.8	279	47	9	1	36	11	3.2	0.9	45	12	1.1	0.3	0.097	0.008	0.21	0.05	1.0	0.1	0.19	0.13	0.051	0.032
LZb	634	580	43	13	373	103	134	56	83	30	44	14	84	18	75	7	2.5	0.7	274	62	14	2	51	6	4.3	0.8	51	11	1.4	0.1	0.241	0.204	0.28	0.06	1.1	0.1	0.29	0.08	0.082	0.024
LZb	558	488	38	4	299	34	133	19	131	63	58	21	92	20	79	13	2.5	0.9	271	35	14	4	52	16	4.2	1.4	48	9	1.4	0.4	0.707	0.392	0.30	0.09	0.98	0.20	0.36	0.16	0.091	0.035
LZb	447	367	34	1	290	31	117	8	130	83	55	29	109	10	83	16	2.8	1.0	289	49	15	5	61	17	5	1	56	15	1.6	0.4	0.117	0.018	0.32	0.06	1.2	0.1	0.37	0.18	0.10	0.05
LZb	346	221	35	1	260	23	236	61	187	92	69	36	88	28	82	19	2.5	1.8	250	58	12	6	57	40	4.8	3.3	43	15	1.5	0.9	0.112	0.031	0.30	0.20	1.1	0.2	0.33	0.30	0.10	0.10
LZb	177	173	28	11	245	80	169	133	114	50	43	17	112	9	71	8	3.6	0.1	299	82	13	3	63	13	6	1	59	10	1.7	0.3	0.420	0.515	0.40	0.05	1.2	0.0	0.42	0.01	0.12	0.01
LZa	161	137	24	1	211	2	98	31	163	23	56	6	122	4	79	3	4.1	0.9	300	14	15	2	68	4	7	1	63	3	1.8	0.1	0.129	0.009	0.45	0.08	1.3	0.1	0.46	0.10	0.13	0.03
LZa	125	107	23	1	227	26	55	12	227	61	70	16	157	44	89	13	4.5	0.5	278	36	18	2	73	4	8	1	63	3	2.0	0.1	0.138	0.005	0.54	0.11	1.3	0.0	0.56	0.06	0.16	0.01
LZa	96	27	24	2	230	9	77	13	152	66	49	12	142	5	80	6	4.1	0.2	316	21	18	2	72	15	8	0	65	3	1.9	0.3	0.137	0.014	0.51	0.05	1.5	0.3	0.57	0.14	0.17	0.04
LZa	7		26		241		85		227		63		131		83		4.6		296		16		62		9		61		1.8		0.178		0.63		1.3		0.67		0.15
Calculated as averages (Ave.) of 3 consecutive samples with 1σ SD for n > 2. Cu was analysed using XRF, while the remaining were by ICP-MS. Missing data reflects either not analysed or below detection limits. Results for W are not given for the 90-22 drill core since these samples was prepared in a wolfram carbide morter. Stratigraphic height is given as high and low referring to the interval used for averaging. Complete data set in Supplementary File S1.

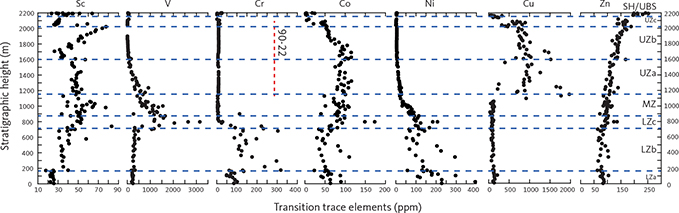
Fig. 34 Transition trace elements (Sc, V, Cr, Co, Ni, Cu and Zn; ppm) as a function of stratigraphic height (m) in the LS. Blue horizontal dashed lines: divisions of the LS. Abbreviations in Fig. 2. Red vertical dashed line: location of drill core 90-22.

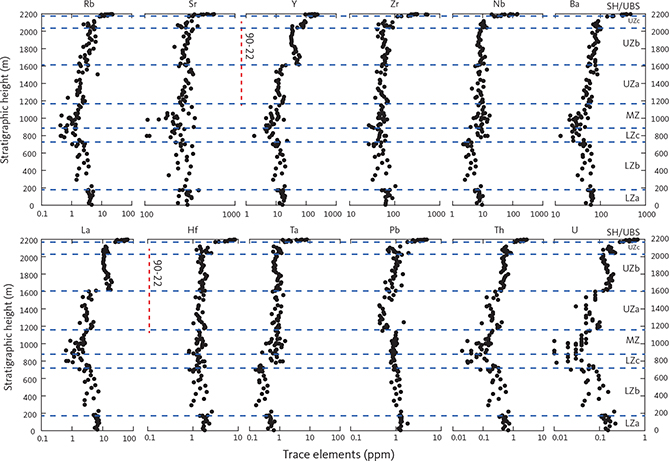
Fig. 35 Selected alkali metal (Rb), alkaline earth (Sr, Ba), high field strength (Y, Zr, Nb, Hf), rare-earth (La) and heavy (Pb, Th, U) trace elements (ppm) as a function of stratigraphic height (m) in the LS. Plotted on a log scale. Blue horizontal dashed lines: divisions of the LS. Abbreviations divisions in Fig. 2. Red vertical dashed line: location of drill core 90-22.

The trace elements can be divided into two groups, those that are dominantly partitioned into the primocryst minerals (included) or into the coexisting melt (excluded; McBirney 1998, 2002). The former, with partition coefficients above unity, will occur in high concentrations in the early-formed gabbros. The latter, with partition coefficients below unity, will be enriched in the residual melt fraction with advanced differentiation and will thus be relatively depleted in the early gabbros. Earlier studies of trace elements in the Skaergaard intrusion include Wager & Mitchell (1951), Haskin & Haskin (1968), Brooks (1969) and Paster et al. (1974).

4.5.2.1 Included trace elements

The included trace elements are particularly well illustrated by the transition metals (Fig. 34). These are highly to partially included elements with bulk-partitioning coefficients often well above unity that are known to be partitioned preferentially into olivine (Ni and Co), magnetite and ilmenite (Sc, V, Cr, Co, Ni and Zn) and pyroxenes (Sc, Cr, Co and Ni; Wager & Mitchell 1951; Paster et al. 1974; McBirney 1998; Jang & Naslund 2003). The concentrations of both the included and excluded trace elements are shown in Table 15.

Despite large scatter in some subzones, the variations for V, Cr and Ni show moderate to strong depletions with stratigraphic height reflecting their preferred partitioning into specific early primocrysts and subzones (Fig. 34). Vanadium is constant at 200–400 ppm in LZa and LZb, followed by a marked enrichment in LZc to >2000 ppm due to the appearance of FeTi oxides as a primocryst. It is terminated by an asymptotic depletion from the base of LZc and into the UZ approaching c. 5 ppm. The UZ variation is caused by the concurrent depletion of V in the coexisting melt as well as the upward decreasing modal abundances, mainly of magnetite (Fig. 15). Chromium shows low concentrations in LZa of 50–100 ppm, followed by an irregular increase in LZb to c. 300 ppm due to the appearance of clinopyroxene. Subsequently, Cr strongly depleted in the LZb and LZc, reaches low concentrations in the MZ and approaches c. 9 ppm in the UZ, again due to the concurrent strong depletion in the melt. Nickel likewise decreases from c. 200 ppm at the base of LZa to the top of the MZ and further into the UZb, where it reaches low concentrations approaching 3 ppm with the consistent appearance of olivine and other mafic minerals throughout the stratigraphy and the concurrent depletion of Ni in the coexisting melt. The high modal abundance of olivine at the base of UZb is not recorded by Ni because of the low melt content of Ni in the iron-rich melts of the UZ. The prominent variations for these highly included elements are strongly depleted (Figs 15, 34) due to early partitioning into olivine (Ni), pyroxene (Cr) and FeTi oxides (V), respectively.

Copper is consistently low at 100–150 ppm from the LZ until the upper part of the MZ where sulphides become saturated (Andersen 2006; Nielsen et al. 2015). Because Cu is strongly partitioned into sulphides (as minerals or immiscible melt), the concentrations in UZa and UZb remain relatively constant (Fig. 34). The variation of Zn, with a systematic upward increase from c. 75 to 150 ppm and a spike in the upper part do not partition into the sulphides to any significant extent.

The variations of Co and Sc differ from the other transition metals because they are partitioned into all mafic and FeTi oxide minerals. Scandium concentration is constantly low in LZa at c. 20 ppm, increases to a relatively constant concentration of about 30–40 ppm in LZb because of the appearance of clinopyroxene, but subsequently becomes highly variable, which is difficult to interpret in terms of the zones and subzones and modal variations. Cobalt similarly records variable concentrations until the base of UZb, where a modest increase may be related to the high modal olivine. Interestingly, Sc (30–70 ppm) and Co (100–50 ppm) show contrasting variations from the base of UZb with a strong increase in Sc and a corresponding decrease in Co that are not easily explained by modal variations, but may suggest behaviour related to liquid immiscibility as in the UZb (Figs 15, 34; see discussions in Sections 5.7.7 and 5.12).

4.5.2.2 Excluded trace elements

The excluded group of elements does not always show systematic variations as a function of stratigraphic position directly relatable to modal content of major silicates and oxide minerals in the zones and subzones (Table 15). The group of elements shown in Fig. 35, plotted on a semi-log scale to easier allow pattern recognition, is preferentially excluded from the solid fraction during crystallisation and thus resides principally in the coexisting melts (including trapped melt). An element is defined as excluded if its bulk partition coefficient is below unity (McBirney 2002). Examples are Rb, Sr, Y, Ba, the rare-earth elements (REE; Table 16) and U that are mostly excluded throughout the LS, although some of these may have partitioning coefficients above unity. An example of the latter is the REE that are excluded in the LZa to UZa, but intermittently or nearly included in UZb, when apatite first appears as a primocryst (Figs 35, 36). Concentrations of excluded trace elements are shown in Tables 15 and 16. See also discussion of bulk-partitioning coefficients in Section 5.11.3.

Table 16 Summary of gabbro REE compositions

Zone	Stratigraphic height (m)		La (ppm)		Ce (ppm)		Pr (ppm)		Nd (ppm)		Sm (ppm)		Eu (ppm)		Gd (ppm)		Tb (ppm)		Dy (ppm)		Ho (ppm)		Er (ppm)		Tm (ppm)		Yb (ppm)		Lu (ppm)
	high	low	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD	Ave.	SD
UBS	2169	2165	56	8	152	28	24	6	117	32	31	9	11	4	29	8	4.8	1.3	30	7	5	1	14	3	1.9	0.4	12	3	1.8	0.4
Uzc	2165	2165	35		98		16		82		23		12		22		3.6		22		4.0		11		1.6		11		1.7
Uzc	2165	2164	57	5	158	13	26	2	132	11	37	3	13	1	35	2	6	1	39	3	7	1	19	2	2.9	0.4	18	2	2.9	0.3
Uzc	2163	2147	37	11	103	28	17	4	85	18	24	5	9	2	23	4	4.0	0.8	25	6	4.7	1.1	13	3	2.0	0.5	13	3	2.1	0.4
Uzc	2144	2141	29		80		13		66		19		6		19		3.3		21		4.1		12		1.8		12		1.9
Uzc	2091	2081	12	1	33	3	6	0	31	2	9	1	4.0	0.3	11	1	1.8	0.1	12	1	2.4	0.2	7	1	1.1	0.1	7	1	1.2	0.1
Uzc	2075	2060	14	0	39	0	6	0	34	1	10	0	3.8	0.3	12	0	2.0	0.1	13	1	2.6	0.0	7	0	1.1	0.0	8	0	1.3	0.1
Uzc	2060	2046	13	2	35	7	6	1	30	7	9	2	3.5	0.1	10	3	1.6	0.5	10	4	2.0	0.8	6	2	0.83	0.40	5	3	0.88	0.45
UZb	2044	2030	15		41		7		34		9		3.8		10		1.5		9		1.7		4.5		0.63		3.8		0.62
UZb	2024	1984	11	0	31	1	5	0	27	2	7	0	3.5	0.2	8	1	1.2	0.0	7	0	1.2	0.0	2.9	0.1	0.39	0.02	2.3	0.2	0.36	0.04
UZb	1962	1921	10	0	29	1	4.8	0	26	1	7	0	3.0	0.1	8	0	1.1	0.0	6	0	1.1	0.0	2.7	0.1	0.34	0.02	2.0	0.1	0.30	0.02
UZb	1902	1862	11	0	31	1	5.0	0	27	0	7	0	3.0	0.1	8	0	1.1	0.0	6	0	1.1	0.0	2.6	0.1	0.33	0.01	1.9	0.1	0.27	0.01
UZb	1843	1801	13	2	37	5	6	1	32	4	9	1	3.1	0.4	9	1	1.3	0.2	7	1	1.3	0.2	3.1	0.4	0.38	0.05	2.2	0.2	0.31	0.03
UZb	1782	1748	14	1	39	4	6	1	34	4	9	1	3.3	0.2	10	1	1.5	0.1	8	1	1.4	0.1	3.4	0.3	0.42	0.03	2.4	0.2	0.33	0.02
UZb	1728	1691	17	3	50	10	8	2	43	9	12	2	3.7	0.6	13	3	1.8	0.4	10	2	1.7	0.3	4.0	0.8	0.48	0.08	2.6	0.3	0.35	0.04
UZb	1671	1630	16	1	45	2	7	0	39	2	11	0	3.4	0.2	12	0	1.7	0.1	9	0	1.6	0.1	3.8	0.2	0.45	0.03	2.5	0.1	0.34	0.02
UZb	1620	1600	9	8	26	23	4.1	3.8	22	21	6	6	2.4	1.2	7	6	1.0	0.8	6	4	1.0	0.7	2.5	1.5	0.32	0.16	1.9	0.7	0.26	0.09
UZa	1561	1527	3.2	0.9	8	2	1.3	0.3	6	1	1.9	0.3	1.7	0.1	2.4	0.3	0.39	0.06	2.2	0.3	0.48	0.06	1.2	0.2	0.16	0.03	1.1	0.2	0.17	0.02
UZa	1506	1431	3.0	1.1	8	3	1.2	0.4	6	2	2.0	0.5	1.5	0.2	2.4	0.5	0.39	0.08	2.3	0.5	0.49	0.09	1.3	0.2	0.18	0.03	1.2	0.2	0.17	0.02
UZa	1403	1343	3.0	0.1	8	0	1.2	0.0	6	0	1.9	0.0	1.4	0.1	2.3	0.0	0.38	0.00	2.2	0.0	0.47	0.01	1.2	0.0	0.17	0.00	1.1	0.0	0.16	0.00
UZa	1323	1282	2.8	0.3	7	1	1.1	0.1	6	0	1.8	0.1	1.2	0.0	2.3	0.2	0.40	0.10	2.1	0.2	0.46	0.03	1.2	0.1	0.17	0.01	1.1	0.1	0.16	0.01
UZa	1268	1237	3.2	1.6	8	4	1.3	0.6	7	3	2.0	0.7	1.3	0.2	2.6	0.7	0.52	0.12	2.5	0.8	0.52	0.14	1.3	0.4	0.19	0.06	1.2	0.3	0.18	0.05
UZa	1218	1188	4.3	0.2	11	0	1.7	0.1	8	0	2.5	0.0	1.4	0.0	3.1	0.1	0.56	0.02	3.0	0.1	0.62	0.02	1.6	0.1	0.23	0.01	1.4	0.0	0.21	0.01
UZa	1178	1131	3.3	0.6	8	2	1.3	0.3	7	1	1.9	0.5	1.2	0.1	2.5	0.6	0.43	0.14	2.2	0.8	0.47	0.15	1.2	0.4	0.17	0.06	1.1	0.4	0.16	0.05
MZ	1098	1055	2.3	0.2	6	0	0.96	0.05	5	0	1.6	0.2	1.0	0.1	2.1	0.2	0.33	0.05	1.8	0.3	0.38	0.07	1.0	0.2	0.13	0.03	0.87	0.18	0.13	0.03
MZ	1053	1032	1.5		4.1		0.71		4.1		1.4		0.85		2.0		0.32		1.8		0.39		1.0		0.13		0.91		0.14
MZ	1024	1009	2.1	0.6	6	2	0.94	0.25	5	1	1.6	0.3	0.98	0.10	2.2	0.3	0.35	0.06	2.0	0.4	0.42	0.08	1.1	0.2	0.14	0.03	0.96	0.18	0.15	0.03
MZ	1003	1002	1.9	0.7	5	2	0.82	0.23	4.5	1.1	1.4	0.4	0.96	0.20	2.0	0.4	0.30	0.08	1.6	0.5	0.35	0.10	0.90	0.29	0.11	0.04	0.78	0.25	0.12	0.04
MZ	988	961	1.8	0.4	5	1	0.92	0.27	5	2	1.8	0.6	0.84	0.06	2.4	0.7	0.38	0.13	2.2	0.9	0.46	0.17	1.2	0.5	0.16	0.07	1.1	0.4	0.16	0.05
MZ	953	930	1.9		5		0.83		4.6		1.4		0.88		2.0		0.30		1.7		0.35		0.91		0.12		0.78		0.12
MZ	921	900	1.4	0.8	3.6	1.9	0.60	0.26	3.5	1.1	1.1	0.2	0.88	0.19	1.6	0.2	0.24	0.02	1.2	0.1	0.28	0.02	0.69	0.05	0.082	0.006	0.59	0.02	0.092	0.005
MZ	890	875	1.2	0.3	3.3	0.6	0.56	0.07	3.3	0.2	1.0	0.0	0.77	0.06	1.6	0.1	0.23	0.01	1.2	0.1	0.27	0.02	0.67	0.05	0.079	0.008	0.58	0.04	0.089	0.006
LZc	847	816	1.5	0.5	4.1	1.3	0.68	0.19	3.8	0.9	1.2	0.3	0.73	0.07	1.7	0.2	0.26	0.05	1.4	0.3	0.31	0.05	0.78	0.16	0.095	0.021	0.67	0.11	0.10	0.01
LZc	808	798	1.1	0.8	3.1	2.0	0.50	0.31	2.8	1.5	0.87	0.45	0.55	0.23	1.4	0.5	0.19	0.09	0.87	0.57	0.21	0.11	0.53	0.27	0.061	0.039	0.47	0.21	0.076	0.028
LZc	784	742	2.5	1.3	7	4	1.1	0.6	6	3	2.0	1.0	0.85	0.19	2.4	1.2	0.41	0.22	2.4	1.5	0.49	0.28	1.3	0.7	0.17	0.11	1.1	0.6	0.17	0.09
LZc	723	703	3.0	0.5	8	1	1.2	0.2	6	1	1.9	0.2	0.96	0.08	2.3	0.2	0.38	0.02	2.1	0.2	0.44	0.03	1.2	0.1	0.15	0.01	1.0	0.1	0.15	0.01
LZb	703	681	2.8	1.2	7	3	1.1	0.4	5	2	1.7	0.3	0.94	0.13	1.9	0.3	0.33	0.04	1.7	0.3	0.37	0.04	0.97	0.11	0.12	0.02	0.84	0.11	0.12	0.01
LZb	634	580	4.2	0.9	11	2	1.7	0.2	8	1	2.4	0.1	1.1	0.1	2.8	0.1	0.46	0.03	2.7	0.3	0.54	0.05	1.4	0.1	0.19	0.02	1.2	0.1	0.18	0.02
LZb	558	488	4.2	1.5	11	4	1.6	0.6	8	3	2.3	0.6	1.1	0.2	2.8	0.6	0.45	0.10	2.6	0.7	0.53	0.13	1.4	0.3	0.21	0.05	1.1	0.3	0.18	0.04
LZb	447	367	5	2	13	5	1.9	0.7	9	3	2.6	0.9	1.2	0.2	2.9	0.9	0.48	0.14	2.8	0.9	0.56	0.16	1.5	0.4	0.20	0.06	1.3	0.3	0.19	0.04
LZb	346	221	4.1	2.7	10	7	1.6	0.9	7	4	2.1	1.0	0.94	0.21	2.4	1.0	0.39	0.16	2.2	1.0	0.45	0.19	1.2	0.5	0.16	0.07	1.1	0.5	0.15	0.06
LZb	177	173	5	0	13	1	2.0	0.2	9	1	2.5	0.4	1.1	0.1	2.7	0.5	0.45	0.08	2.5	0.6	0.50	0.11	1.3	0.3	0.18	0.04	1.1	0.2	0.17	0.03
LZa	161	137	6	1	15	2	2.3	0.2	11	1	2.8	0.3	1.2	0.0	3.1	0.3	0.49	0.04	2.8	0.3	0.56	0.05	1.5	0.1	0.20	0.02	1.3	0.1	0.19	0.02
LZa	125	107	7	1	18	1	2.6	0.2	12	1	3.2	0.3	1.2	0.0	3.5	0.2	0.56	0.04	3.2	0.3	0.63	0.05	1.7	0.1	0.23	0.02	1.5	0.2	0.21	0.02
LZa	96	27	7	1	17	1	2.5	0.2	12	1	3.1	0.3	1.3	0.1	3.4	0.3	0.54	0.05	3.1	0.3	0.63	0.05	1.7	0.1	0.23	0.02	1.4	0.1	0.21	0.02
LZa	7		7		16		2.4		11		3.0		1.2		3.2		0.51		2.9		0.58		1.5		0.21		1.3		0.19
Calculated as averages (Ave.) of three consecutive samples with 1σ SD for n > 2. Missing data reflects either not analysed or results below detection limits. Stratigraphic height is given as high and low referring to the interval used for averaging. Complete data set in Supplementary File S1.

Fig. 36 Selected rare earth element (La_N and Yb_N) concentrations (ppm) and Sm/Yb ratio normalised to normal MORB composition (Sun & McDonough 1989) as a function of stratigraphic height (m) in the LS. Plotted on a log scale. Blue horizontal dashed lines: divisions of the LS. Abbreviations in Fig. 2. Red vertical dashed line: location of drill core 90-22. REE: rare earth elements. MORB: Mid-Ocean Ridge Basalt. N: normalised to normal MORB.

Observable patterns in trace element variations correlate with stratigraphic height and subzone mineralogy (Fig. 35). Most of the elements show a systematic upward decrease in the LZa to LZc, exemplified by Rb that varies from 4 ppm at the base of LZa to 2 ppm in the upper part of LZc. The systematic decrease in these elements is interpreted to record the concurrent decrease in the trapped liquid content (e.g. Henderson 1970, 1975; Tegner et al. 2009) that appears to mask any expected upward increases in the coexisting residual magma due to the low bulk partition of these elements. The correlations between the trapped melt content versus Rb and La in the LZ are illustrated in Fig. 37 according to estimates of trapped melt content made by Tegner et al. (2009).

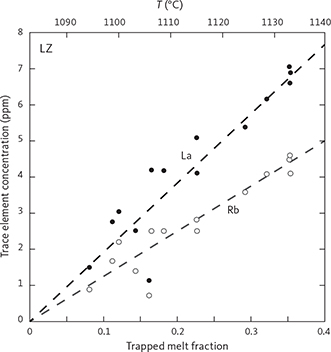
Fig. 37 Selected trace elements (Rb and La) concentrations (ppm) as a function of the trapped melt content in the LS (Tegner et al. 2009). Corresponding melt temperature (T) is shown at the top of graph (Thy et al. 2009b, 2013).

The effect of FeTi oxide crystallisation in the LZc can be seen in most of the excluded elements as decreasing concentrations (Rb, Sr, Y, Ba, La and other REE, Th and U). This observation can be attributed to the low concentrations of these elements and the high modal amount (<20–30 wt%) of FeTi oxides in LZc (Fig. 15) and the low trapped-melt content in LZc documented by Tegner et al. (2009), but may also be related to the observed reduction in grain size (Fig. 5). In contrast, the Nb and Ta concentrations are positively affected by FeTi oxide crystallisation in LZc, where Nb increases from about 3 ppm to 8 ppm and Ta increases from 0.3 ppm to 0.9 ppm, reflecting partitioning of these elements into ilmenite and to a lesser extent magnetite.

One group of elements is approximately constant throughout the main part of the upper stratigraphy (UZa to UZb): c. 50–60 ppm Zr, c. 8–12 ppm Nb, c. 1–2 ppm Hf and c. 0.61–1 ppm Ta. Yttrium and lanthanum (and the other REE) abruptly increase in UZb (Fig. 36) related to the appearance of apatite (Fig. 14) and followed by a modest upward decrease. The Sm/Yb ratio shows marked increase upward in the UZb (Fig. 36, normalised to typical mid-ocean ridge basalt (MORB) concentration). REE patterns are further illustrated in detail in Fig. 38 as normalised variations showing increasing steps in concentrations narrowly located at the UZa–UZb boundary both for the light (La_N) and heavy (Yb_N) REE. The UZb gabbros transgress the UZc gabbros (Fig. 38) due to the change in slopes at the UZa–UZb boundary (Fig. 36). The systematically gently sloping patterns for the normalised REE are similarly consistent in the three individual UZ subzones, but with positive Eu-anomalies only for UZa gabbros (Fig. 38A), probably related to the lower plagioclase content in UZb and UZc compared to UZa.

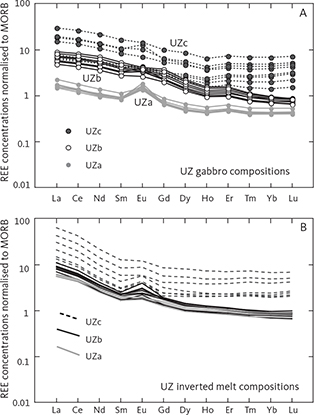
Fig. 38 Rare earth elements (REE) of UZ normalised to normal MORB (log scale; Sun & McDonough, 1989). A: Gabbro compositions. B: Inverted melt compositions. Data are grouped as: UZc, UZb and UZa.

A small group of elements (Rb, Sr and Ba) suggests systematic, but small, increases upward with some noticeable exceptions, such as a small reduction for Rb at the base of UZa and in Sr at the base of UZb, the latter can be related to high olivine and low plagioclase contents commencing at the base of this zone. Finally, and unexplainably, there is a drop in Pb, Th and U in the central part of UZa (Fig. 35).

Most excluded element variations are capped by increasing and high concentrations in the UZc approaching the SH (Fig. 35). For example, 10–20 ppm Rb, 320–570 ppm Sr, 150–220 ppm Y, 120–400 ppm Zr and 160–350 ppm Ba. This is likely related to extreme differentiation of the residual magma and to the high amount of granophyric melt in UZc (Figs 13, 14). For Zr, the concentration has been sufficiently high in the melt to precipitate “rather abundant” zircon near the top of the UZc, as noted by Wager & Brown (1967).

In summary, three important variables control excluded element behaviour in the gabbros as a function of stratigraphy, as follows:

(1) Trapped melt content partly controls the behaviour of the excluded elements with low bulk partition coefficients. This is particularly obvious in the upward decrease in several elements in the LZa and LZb that is positively correlated with the trapped melt content. Another possible effect of high melt content is in the upper part of the UZc where the trapped melt contributes to the bulk partition coefficient by a melt-partition coefficient of unity, thus higher trapped melt content leads to higher contents of excluded elements.

(2) The modal content of specific zones and subzones affects the trace element content by either increasing or decreasing the concentrations dependent on the specific partitioning coefficients. Examples of such strong effects on the trace element concentrations are the appearances of apatite in UZb and FeTi oxides in the LZc. In the latter, high partition results in an increase (Ta and Nb) and low partition coefficients result in a decrease (Rb, Ba and REE).

(3) Fractional crystallisation results in a systematic upward increase in the main magma chamber for elements with low partition and reversely a decrease of elements with high partitioning coefficients. Crystallisation and trapping of melt from such an evolving main chamber result in systematic variation in the solid fraction. Depending on the bulk partition coefficients, the variation in the gabbros as a function of stratigraphy will vary so that low partition will result in increasing concentrations, unity partition (c. 1) will result in constant variations, and finally, high partition will result in decreasing variations upward in the stratigraphy. Examples of this are several elements (Zr, Nb, Hf and Ta) that suggest near constant variations upward from LZc through UZc, while other elements (Rb and Ba) show a steady increase upward in the same stratigraphic intervals. The included elements V, Cr and Ni are examples of elements with high partition coefficients that decrease upward with stratigraphic position dependent of the magnitude of the partition coefficients.

4.5.3 Co-variation of mineral modes and trace element concentrations

The Pearson correlation coefficients between the calculated modal mineralogy and trace element concentrations are shown in Table 17 for both the lower (LZ–UZa) and the upper (UZb–UZc) LS. In the upper part of the LS, there is a remarkably high positive interdependency between all the excluded elements (including Zn). The same group of elements is negatively correlated with F. This shows that the excluded elements behave in a similar fashion being partially excluded from the solid fraction and increasing upward in the melt stratigraphy (towards lower values of F and T). The same group of excluded trace elements in the same stratigraphic section is negatively correlated with the modal amount of plagioclase, magnetite, ilmenite and apatite, but positively correlated with quartz and orthoclase. This suggests that the increase in the excluded elements in the upper part of the intrusion may be associated with an evolved melt component and not with the predominantly silicate and oxide building blocks of the gabbros.

Table 17 Pearson product moment correlation coefficient (r) matrices for mineral modes and selected trace elements

	Subzones Uzc and UZb
	F	Ol	Opx	Cpx	Pl	Mt	Il	Ap	Q	Or	Co	Sc	V	Cr	Ni	Zn	Rb	Sr	Y	Zr	Nb	Ba	La	Ce	Nd	Sm	Eu	Gd	Dy	Ho	Er	Tm	Yb	Lu	Hf	Ta	Pb	Th	U
F	1.00
Ol	–0.03	1.00
OPX
CPX	–0.55	–0.62		1.00
PL	0.56	0.17		–0.70	1.00
Mt	0.87	–0.18		–0.41	0.38	1.00
Il	0.83	0.34		–0.58	0.33	0.71	1.00
Ap	0.81	0.44		–0.72	0.43	0.66	0.93	1.00
Q	–0.58	–0.15		0.18	–0.46	–0.46	–0.64	–0.56	1.00
Or	–0.64	–0.12		0.34	–0.66	–0.44	–0.52	–0.52	0.74	1.00
Co	0.94	0.13		–0.63	0.70	0.75	0.80	0.80	–0.63	–0.82	1.00
Sc	–0.06	0.11		–0.23	0.48	–0.07	–0.24	–0.20	–0.04	–0.15	0.07	1.00
V	0.39	–0.57		0.21	–0.31	0.54	0.25	0.10	0.08	0.26	0.10	–0.28	1.00
Cr	–0.14	0.11		–0.20	0.29	–0.13	–0.22	–0.14	0.06	0.16	–0.10	0.13	–0.39	1.00
Ni	0.62	0.02		–0.44	0.43	0.62	0.54	0.52	–0.43	–0.16	0.50	0.35	0.46	–0.03	1.00
Zn	–0.64	–0.13		0.35	–0.59	–0.46	–0.52	–0.55	0.66	0.94	–0.78	0.03	0.18	0.19	–0.14	1.00
Rb	–0.67	–0.07		0.25	–0.50	–0.50	–0.58	–0.56	0.73	0.97	–0.81	0.01	0.12	0.28	–0.15	0.95	1.00
Sr	–0.56	–0.14		0.18	–0.32	–0.40	–0.53	–0.48	0.59	0.88	–0.69	0.06	0.10	0.48	0.00	0.88	0.94	1.00
Y	–0.62	–0.08		0.44	–0.82	–0.44	–0.39	–0.44	0.62	0.92	–0.79	–0.29	0.28	–0.10	–0.27	0.90	0.85	0.69	1.00
Zr	–0.52	–0.13		0.17	–0.40	–0.36	–0.48	–0.45	0.67	0.91	–0.69	–0.10	0.19	0.37	–0.07	0.84	0.94	0.94	0.73	1.00
Nb	–0.51	–0.07		0.23	–0.56	–0.34	–0.35	–0.38	0.62	0.90	–0.67	–0.06	0.24	0.08	–0.12	0.96	0.89	0.79	0.92	0.78	1.00
Ba	–0.59	–0.11		0.23	–0.49	–0.42	–0.51	–0.49	0.69	0.97	–0.76	–0.04	0.19	0.30	–0.09	0.94	0.99	0.96	0.84	0.97	0.90	1.00
La	–0.50	0.01		0.19	–0.62	–0.33	–0.31	–0.32	0.65	0.94	–0.68	–0.15	0.27	0.04	–0.10	0.94	0.91	0.79	0.95	0.81	0.98	0.91	1.00
Ce	–0.49	0.02		0.18	–0.62	–0.33	–0.30	–0.30	0.64	0.93	–0.67	–0.16	0.27	0.04	–0.10	0.94	0.90	0.79	0.95	0.81	0.98	0.91	1.00	1.00
Nd	–0.49	0.02		0.18	–0.62	–0.33	–0.28	–0.29	0.63	0.93	–0.66	–0.17	0.26	0.05	–0.10	0.94	0.89	0.79	0.94	0.80	0.98	0.91	1.00	1.00	1.00
Sm	–0.51	0.01		0.22	–0.64	–0.34	–0.30	–0.31	0.63	0.93	–0.68	–0.18	0.26	0.05	–0.12	0.94	0.90	0.79	0.95	0.81	0.98	0.91	1.00	1.00	1.00	1.00
Eu	–0.58	–0.06		0.24	–0.56	–0.41	–0.44	–0.43	0.66	0.97	–0.75	–0.11	0.19	0.25	–0.12	0.97	0.97	0.92	0.90	0.91	0.95	0.98	0.96	0.96	0.96	0.96	1.00
Gd	–0.50	0.02		0.22	–0.66	–0.34	–0.27	–0.29	0.61	0.92	–0.67	–0.22	0.26	0.04	–0.13	0.93	0.88	0.77	0.96	0.78	0.97	0.89	0.99	1.00	1.00	1.00	0.95	1.00
Dy	–0.59	–0.05		0.35	–0.74	–0.41	–0.37	–0.40	0.64	0.94	–0.76	–0.24	0.26	–0.01	–0.22	0.94	0.89	0.76	0.99	0.78	0.96	0.89	0.98	0.98	0.98	0.99	0.95	0.99	1.00
Ho	–0.62	–0.08		0.41	–0.77	–0.44	–0.40	–0.44	0.64	0.94	–0.79	–0.26	0.25	–0.03	–0.26	0.93	0.87	0.74	0.99	0.76	0.95	0.87	0.97	0.97	0.97	0.97	0.93	0.98	1.00	1.00
Er	–0.64	–0.10		0.45	–0.80	–0.46	–0.42	–0.47	0.64	0.93	–0.81	–0.28	0.25	–0.06	–0.29	0.92	0.86	0.72	1.00	0.75	0.93	0.86	0.95	0.95	0.95	0.96	0.92	0.96	0.99	1.00	1.00
Tm	–0.67	–0.12		0.50	–0.82	–0.49	–0.45	–0.51	0.64	0.93	–0.83	–0.28	0.25	–0.07	–0.32	0.91	0.86	0.71	1.00	0.74	0.91	0.85	0.93	0.93	0.93	0.94	0.90	0.94	0.98	0.99	1.00	1.00
Yb	–0.69	–0.14		0.53	–0.83	–0.50	–0.48	–0.53	0.64	0.93	–0.85	–0.29	0.24	–0.06	–0.33	0.91	0.86	0.72	0.99	0.75	0.90	0.85	0.92	0.92	0.92	0.93	0.90	0.93	0.98	0.99	0.99	1.00	1.00
Lu	–0.71	–0.16		0.56	–0.84	–0.53	–0.51	–0.56	0.64	0.92	–0.87	–0.30	0.22	–0.05	–0.36	0.90	0.85	0.71	0.98	0.74	0.88	0.84	0.90	0.90	0.90	0.91	0.89	0.91	0.96	0.98	0.99	1.00	1.00	1.00
Hf	–0.54	–0.12		0.18	–0.42	–0.37	–0.49	–0.46	0.69	0.94	–0.70	–0.08	0.19	0.37	–0.08	0.88	0.96	0.96	0.77	0.99	0.83	0.98	0.85	0.85	0.84	0.85	0.94	0.82	0.82	0.80	0.79	0.78	0.78	0.78	1.00
Ta	–0.48	–0.05		0.19	–0.54	–0.33	–0.33	–0.35	0.62	0.89	–0.64	–0.08	0.23	0.12	–0.13	0.95	0.89	0.80	0.90	0.78	1.00	0.90	0.97	0.98	0.98	0.98	0.95	0.97	0.96	0.94	0.92	0.90	0.88	0.86	0.83	1.00
Pb	–0.62	–0.09		0.19	–0.48	–0.44	–0.57	–0.53	0.81	0.96	–0.75	0.04	0.16	0.24	–0.15	0.94	0.98	0.91	0.83	0.92	0.90	0.97	0.91	0.91	0.90	0.90	0.96	0.88	0.88	0.86	0.85	0.84	0.84	0.83	0.95	0.90	1.00
Th	–0.63	–0.08		0.24	–0.52	–0.46	–0.55	–0.52	0.75	0.98	–0.79	–0.07	0.16	0.29	–0.17	0.94	0.99	0.94	0.85	0.96	0.89	0.99	0.91	0.91	0.90	0.91	0.97	0.89	0.89	0.88	0.87	0.86	0.87	0.86	0.98	0.89	0.98	1.00
U	–0.57	–0.06		0.19	–0.52	–0.40	–0.47	–0.44	0.72	0.97	–0.74	–0.15	0.19	0.29	–0.14	0.92	0.98	0.92	0.86	0.96	0.89	0.99	0.93	0.92	0.92	0.92	0.98	0.91	0.90	0.89	0.87	0.86	0.86	0.85	0.98	0.89	0.97	0.99	1.00
	Subzones Uza to LZc
	F	Ol	Opx	Cpx	Pl	Mt	Il	Ap	Q	Or	Co	Sc	V	Cr	Ni	Zn	Rb	Sr	Y	Zr	Nb	Ba	La	Ce	Nd	Sm	Eu	Gd	Dy	Ho	Er	Tm	Yb	Lu	Hf	Ta	Pb	Th	U
F	1.00
Ol	0.27	1.00
OPX	0.89	0.23	1.00
CPX	–0.74	–0.47	–0.73	1.00
PL	0.57	0.32	0.65	–0.69	1.00
Mt	–0.48	–0.33	–0.66	0.34	–0.63	1.00
Il	–0.50	–0.38	–0.62	0.36	–0.82	0.66	1.00
Ap	0.29	0.44	0.22	–0.33	0.21	–0.15	–0.22	1.00
Q
Or
Co	–0.64	–0.05	–0.72	0.39	–0.74	0.65	0.80	–0.15			1.00
Sc	–0.78	–0.53	–0.76	0.86	–0.87	0.52	0.72	–0.38			0.61	1.00
V	–0.25	–0.42	–0.47	0.32	–0.73	0.68	0.82	–0.12			0.60	0.58	1.00
Cr	0.50	0.04	0.54	–0.27	0.51	–0.48	–0.58	0.47			–0.61	–0.47	–0.27	1.00
Ni	0.91	0.27	0.77	–0.67	0.36	–0.31	–0.31	0.29			–0.39	–0.65	0.00	0.49	1.00
Zn	–0.77	0.02	–0.75	0.40	–0.57	0.58	0.61	–0.22			0.90	0.54	0.33	–0.70	–0.61	1.00
Rb	0.67	0.57	0.71	–0.67	0.75	–0.65	–0.72	0.22			–0.57	–0.83	–0.73	0.27	0.51	–0.43	1.00
Sr	0.23	0.46	0.35	–0.52	0.86	–0.45	–0.74	0.20			–0.54	–0.73	–0.81	0.22	0.01	–0.23	0.69	1.00
Y	0.45	0.50	0.56	–0.27	0.52	–0.66	–0.75	0.15			–0.52	–0.56	–0.76	0.20	0.26	–0.33	0.82	0.52	1.00
Zr	0.54	0.37	0.52	–0.46	0.25	–0.39	–0.22	0.06			–0.16	–0.48	–0.34	–0.08	0.41	–0.14	0.70	0.19	0.70	1.00
Nb	–0.31	–0.16	–0.33	0.15	–0.54	0.30	0.70	–0.31			0.61	0.43	0.29	–0.72	–0.28	0.58	–0.20	–0.37	–0.22	0.28	1.00
Ba	0.28	0.57	0.42	–0.48	0.76	–0.56	–0.74	0.19			–0.45	–0.72	–0.85	0.16	0.08	–0.15	0.85	0.90	0.78	0.50	–0.22	1.00
La	0.75	0.56	0.78	–0.67	0.74	–0.64	–0.76	0.28			–0.61	–0.87	–0.70	0.31	0.57	–0.49	0.95	0.64	0.87	0.75	–0.27	0.80	1.00
Ce	0.75	0.56	0.78	–0.67	0.73	–0.65	–0.76	0.28			–0.62	–0.86	–0.70	0.31	0.57	–0.50	0.95	0.63	0.88	0.76	–0.27	0.80	1.00	1.00
Nd	0.71	0.55	0.75	–0.60	0.69	–0.66	–0.76	0.24			–0.60	–0.81	–0.71	0.28	0.52	–0.48	0.94	0.60	0.92	0.77	–0.25	0.80	0.99	0.99	1.00
Sm	0.65	0.55	0.71	–0.50	0.65	–0.68	–0.78	0.23			–0.60	–0.74	–0.74	0.28	0.46	–0.46	0.92	0.59	0.96	0.75	–0.27	0.80	0.97	0.98	0.99	1.00
Eu	–0.10	0.48	0.10	–0.17	0.52	–0.41	–0.56	0.02			–0.21	–0.39	–0.81	–0.10	–0.29	0.17	0.61	0.80	0.67	0.34	–0.04	0.91	0.54	0.54	0.56	0.60	1.00
Gd	0.56	0.52	0.62	–0.40	0.56	–0.63	–0.72	0.15			–0.53	–0.65	–0.72	0.15	0.36	–0.37	0.87	0.54	0.98	0.77	–0.17	0.78	0.93	0.93	0.97	0.98	0.63	1.00
Dy	0.47	0.49	0.57	–0.29	0.52	–0.65	–0.74	0.14			–0.53	–0.57	–0.75	0.17	0.27	–0.34	0.83	0.52	1.00	0.72	–0.20	0.77	0.88	0.89	0.93	0.97	0.66	0.99	1.00
Ho	0.41	0.51	0.51	–0.25	0.49	–0.63	–0.72	0.13			–0.48	–0.54	–0.76	0.13	0.21	–0.29	0.81	0.53	1.00	0.71	–0.18	0.79	0.86	0.87	0.91	0.95	0.70	0.98	1.00	1.00
Er	0.43	0.50	0.53	–0.25	0.50	–0.64	–0.73	0.14			–0.49	–0.54	–0.75	0.15	0.22	–0.30	0.81	0.52	1.00	0.71	–0.20	0.78	0.86	0.87	0.91	0.95	0.68	0.98	1.00	1.00	1.00
Tm	0.38	0.53	0.49	–0.22	0.48	–0.64	–0.73	0.13			–0.46	–0.52	–0.76	0.14	0.19	–0.28	0.79	0.52	0.99	0.69	–0.21	0.78	0.84	0.85	0.89	0.94	0.70	0.97	0.99	0.99	0.99	1.00
Yb	0.40	0.50	0.51	–0.24	0.48	–0.63	–0.70	0.13			–0.45	–0.52	–0.76	0.13	0.20	–0.26	0.81	0.51	0.99	0.72	–0.15	0.78	0.85	0.86	0.90	0.94	0.70	0.97	0.99	1.00	1.00	0.99	1.00
Lu	0.35	0.49	0.47	–0.20	0.45	–0.62	–0.69	0.11			–0.43	–0.48	–0.76	0.09	0.15	–0.23	0.78	0.50	0.99	0.71	–0.13	0.77	0.83	0.83	0.88	0.93	0.72	0.96	0.99	1.00	0.99	0.99	1.00	1.00
Hf	0.56	0.36	0.53	–0.45	0.22	–0.41	–0.20	0.07			–0.16	–0.46	–0.31	–0.08	0.45	–0.16	0.70	0.15	0.69	0.99	0.31	0.47	0.75	0.75	0.77	0.75	0.31	0.76	0.72	0.70	0.71	0.68	0.72	0.70	1.00
Ta	–0.59	–0.10	–0.58	0.33	–0.58	0.37	0.70	–0.31			0.75	0.55	0.25	–0.77	–0.54	0.77	–0.31	–0.30	–0.27	0.11	0.93	–0.18	–0.40	–0.40	–0.38	–0.37	0.09	–0.27	–0.26	–0.22	–0.24	–0.22	–0.19	–0.15	0.12	1.00
Pb	0.91	0.13	0.88	–0.68	0.52	–0.45	–0.45	0.19			–0.70	–0.66	–0.20	0.47	0.78	–0.76	0.55	0.18	0.38	0.44	–0.28	0.21	0.64	0.65	0.62	0.56	–0.14	0.49	0.41	0.34	0.35	0.30	0.32	0.28	0.46	–0.58	1.00
Th	0.78	0.55	0.78	–0.67	0.71	–0.62	–0.73	0.28			–0.58	–0.86	–0.66	0.32	0.62	–0.50	0.94	0.60	0.84	0.73	–0.24	0.76	0.98	0.98	0.97	0.94	0.49	0.90	0.85	0.82	0.82	0.80	0.81	0.78	0.73	–0.39	0.65	1.00
U	0.76	0.57	0.77	–0.69	0.71	–0.61	–0.72	0.28			–0.57	–0.87	–0.66	0.30	0.59	–0.47	0.93	0.61	0.85	0.77	–0.23	0.78	0.99	0.99	0.98	0.95	0.52	0.91	0.86	0.84	0.84	0.81	0.83	0.80	0.76	–0.37	0.65	0.98	1.00
F: melt remaining. Ol: olivine mode. Opx: orthopyroxene mode. Cpx: clinopyroxene mode. Pl: plagioclase mode. Mt: magnetite mode. Il: ilmenite mode. Ap: apatite mode. Q: quartz mode. Or: orthoclase mode. Mineral modes after Table 2 and trace element concentrations after Tables 14 and 15.

The lower part of the LS shows mixed results, probably due to the complexity of this gabbro sequence that consists of several zones and subzones. Again, the excluded elements show positive interdependency, except for a negative correlation between both Ta and Nb and the rest of the group. These two elements are further positively correlated to ilmenite, magnetite and clinopyroxene (Table 17).

Most included elements are negatively correlated with the excluded elements, except Cr and Ni that are weakly positively correlated. Furthermore, the excluded elements are once again positively correlated with F, meaning that they are increasing upward in the stratigraphy due to differentiation. This indicates a decoupled evolution of the two groups of included and excluded trace elements controlled by differences in their bulk partition coefficients (see discussion in Section 5.11).

There are no strong positive correlations in the LZ to UZa between trace element concentrations and mineral modes, except for Sr and Ba in plagioclase and Sc in clinopyroxene. Remarkably, olivine and apatite do not show strong positive correlations with any trace elements (included or excluded). For apatite, this probably reflects the low modal content of this mineral, while for olivine, most included elements are variably partitioned into all mafic and FeTi oxide minerals. It is furthermore unexpected that the included transition elements do not appear to act as a coherent group of elements with strong positive intra-correlations.

5 Discussion

5.1 Liquidus temperatures

There have been several attempts to estimate the liquidus temperatures of the Skaergaard intrusion. Experimental methods have constrained the upper bracket by determining the liquidus conditions for several potential initial melt compositions. Wager (1960, 1961) identified a sample interpreted as a chilled margin of the intrusion and, thus, representative of the Skaergaard magma. Tilley et al. (1963) and Biggar (1974) melted this sample at atmospheric pressure using a NNO oxygen buffer and determined the liquidus at 1230 ± 16°C, co-saturated with olivine and plagioclase. Subsequent petrographic studies (McBirney 1975, 1996) identified a more suitable chilled margin sample that was found to have plagioclase on the liquidus at 1175 ± 5°C for the magnetite-wüstite (MW) oxygen buffer (Hoover 1989a). Snyder et al. (1993) melted the same chilled margin within the stability field of FeTi oxides (1091–1062°C). Toplis & Carroll (1995) and Thy et al. (2006) used chilled margins of dykes from a swarm believed to be associated with the Skaergaard intrusion (FG-1 dyke swarm; Brooks & Nielsen 1978, 1990). Toplis & Carroll (1995) investigated an oxide mixture approximating the C-dyke composition (lacking MnO and P₂O₅) and found that plagioclase and olivine appeared on the liquidus at 1162 ± 4°C. Thy et al. (2006) bracketed the liquidus for the actual chilled margin of the same dyke at 1171 ± 3°C and found plagioclase at the liquidus, followed by near co-saturation of olivine and clinopyroxene at 1149 ± 10°C. McBirney & Naslund (1990) melted a series of gabbros considered representative of the LS between 1150°C (LZa) and 1002°C (UZc) at various values of T and fO₂ estimated by Morse et al. (1980) and Williams (1971), and thus do not provide independent temperature estimates.

The lower temperature bracket for the UZc was constrained by Tilley et al. (1963) using direct crystallisation experiments on a fayalitic diorite from the middle of UZc (Wager & Brown 1967). They found plagioclase on the liquidus at 1035°C, with bustamite and ferrohedenbergite subsequently appearing at 1010°C and inferred the liquidus temperature to have been above the 970°C inversion of ferrobustamite to ferrohedenbergite (Yoder et al. 1963) and below the 1035°C plagioclase liquidus of the ferrodiorite. Lindsley et al. (1969) used the ferrobustamite-ferrohedenbergite and the tridymite-quartz inversions to further constrain crystallisation temperatures of 980–950°C for the SH at a pressure of 600 ± 100 bars. These experimental constraints suggest that the liquidus temperatures for Skaergaard magma decreased by 206–265°C from its initial emplacement to final solidification represented by the SH, depending on the choice of initial magma composition.

Forward modelling results of Toplis & Carroll (1996) and Thy et al. (2006, 2008, 2009a) largely recorded the above-quoted experimental temperatures for the respective initial melt compositions, but were unable to constrain the terminal liquidus temperature. Ariskin (2002, 2003) used a crystallisation model based on existing experimental low-pressure information for basaltic systems to constrain the temperature variation in the Skaergaard intrusion. His conclusion was that the initial magma filling the chamber was olivine and plagioclase-phyric, which in the LZa had equilibrated at 1145°C.

Several other attempts to constrain the temperature bracket for the Skaergaard intrusion have with various successes been attempted. Hess (1941) estimated a bracket of 185°C, constrained at high temperature (c. 1140°C) by the ortho- to clinopyroxene inversion and at low temperature (955°C) by the hedenbergite-ferrobustamite inversion. Williams (1971) used olivine-pyroxene-oxide equilibria of cumulates as well as Lindsley et al.’s (1969) terminal liquidus temperature to suggest a bracket of c. 400°C (1300–900°C), apparently including the large HZ of Wager & Deer (1939). The temperature bracket of 370°C (1320–950°C) estimated by Kudo & Weill (1970) was based on experimental plagioclase-liquid thermometry and again extrapolated to include the large HZ originally suggested by Wager & Deer (1939). By restricting the bracket of Kudo & Weill (1970) to the exposed cumulate column, a range of 270°C (1220–950°C) is obtained. This estimate is rather close to that of Morse et al. (1980) suggesting 300°C (1250–950°C), based on the plagioclase temperatures determined of Kudo & Weill (1970) and a terminal liquidus temperature of 950°C (Lindsley et al. 1969).

Further attempts to constrain liquidus temperatures for Skaergaard have relied on single- and two-mineral geothermometers (Fig. 39). Morse (2008a) used a 5 kbar study of the Kiglapait intrusion to model the plagioclase liquidus of the Skaergaard intrusion using the plagioclase compositions of Toplis et al. (2008). This suggested LZa/LZb liquidus temperature of 1173°C or extrapolated to the HZ of 1211°C (both temperatures adjusted to atmospheric pressure). Thy et al. (2009b) proposed an empirical single-mineral plagioclase thermometer based on a large data set of melting experiments for North Atlantic basalts with coexisting plagioclase and melt at atmospheric pressure. They obtained a liquidus temperature of 1155°C for the HZ, falling to 1140°C in the LZb, 1050°C in the UZc and finally 1000–1025°C in the SH. These terminal temperatures were similar to those predicted by Morse (2008a), liquidus temperatures from the Thy et al. (2009b) plagioclase geothermometer for the HZ and much of the LS and is >50°C below those estimated using the Morse (2008a) geothermometer (Fig. 39).

Fig. 39 Summary of calculated equilibrium temperatures (T; °C) using single- and two-phase thermometers as a function of stratigraphic height (m) in the LS. Plagioclase temperature (T = 3.6 × An + 899) is obtained using the formula of Thy et al. (2009b), with a 1σ SD based on multiple analyses of plagioclase grains. The extension to 920°C for albite (Ab) is taken to represent the crystallisation of the interstitial granophyre. Olivine and augite temperatures are calculated using linear regressions of the same experimental dataset of Thy et al. (2006), respectively, T = 3.4 × Fo + 910 (ΣR² = 0.943) and T = 5.4% × Mg# + 750 (ΣR² = 0.872), assuming all iron is Fe²⁺. The coexisting augite-olivine temperature is obtained using the formula of Loucks (1996). The coexisting pigeonite-augite temperature is after Putirka (2008; their eq. 37), recommended for pyroxenes with a magnesium number (Mg#) < 0.75. Equilibrium temperatures for coexisting magnetite-ilmenite are from Table 9, calculated using the formula of Ghiorso & Evans (2008). The LZc–MZ interval discussed in the text is shown in the centre of the diagram. The mineral compositions used for the calculations of crystallisation temperatures are from Tables 3–5, 8 and 9. Pl: plagioclase. Ol: olivine. Aug: augite. Pi: pigeonite. Mt: magnetite. Il: ilmenite.

Because of sluggish reaction kinetics and difficulties in attaining and demonstrating equilibrium of plagioclase, specifically in dry melting experiments and at low temperatures, attention is required when products are evaluated and when experimental plagioclase compositions are used in petrogenetic modelling, as in this study (Johannes & Koepke 2001; Morse 2010). Attention to this problem was highlighted by Morse (2010) and subsequently addressed by Thy et al. (2013) for the Skaergaard dyke experiments used here. The study by Thy et al. (2013) on the effects of non-equilibrium or unreactive plagioclase grains in melting experiments provided tighter bounds on experimental plagioclase composition and documented composition-dependent partitioning of Na and Ca between plagioclase and melt. Application of the results to model the Skaergaard, however, requires only minor adjustments to the previously proposed liquidus temperatures and liquid line of descent modelling that does not significantly change the temperature constraints.

Liquidus temperatures from Thy et al. (2009b) are preferred here because they conform to the existing melting experiment on probable initial melt compositions as outlined above (1162–1175°C). Similar single-mineral thermometers formulated for olivine and clinopyroxene using the experimental results for the Skaergaard dykes of Thy et al. (2006) obtain temperatures for the base of LZa of 1117°C and 1136°C, respectively, comparable to the 1137°C plagioclase liquidus temperature determined by Thy et al. (2009b; see caption to Fig. 39).

A single-mineral clinopyroxene thermometer reformulated by Putirka (2008, their Eq. 32d) reproduces the expected temperatures for the two end members from plagioclase compositions reasonably well, but fails to give meaningful results for the intermediate pyroxenes. The reason for this may be related to the unusual low-octahedral occupancy of Al for the Skaergaard pyroxenes. The temperatures obtained using the two-mineral clinopyroxene-olivine thermometer formulated by Loucks (1996) give comparable results to the single-mineral temperatures, while the pigeonite-augite thermometer reformulated by Putirka (2008) deviates significantly (Fig. 39).

The results for the various temperature estimates are compared in Fig. 39 as a function of stratigraphic height. The plagioclase estimates are systematically higher throughout the LS than those based on the mafic minerals. Compared to plagioclase, the mafic minerals (olivine and pyroxenes) record lower equilibration temperatures in LZa and LZb. In addition, the equilibration temperatures in the UZ markedly decrease upward into UZc where the estimates of clinopyroxene temperature drops. The two-pyroxene thermometer (Pi-Aug; pigeonite-augite) records equilibration temperatures of 1100–1075°C in the LZ and into MZ. All the mafic mineral thermometers (olivine (Ol), augite (Au) and Au-Ol) show corresponding and decreasing results upward in the UZ (Fig. 39). If the plagioclase thermometer is applied to the albitic plagioclase (Ab) in the granophyre (Figs 13, 14), a terminal temperature is obtained down to c. 920°C, largely conforming to that obtained for olivine and based on the same melting experiments. The apatite saturation temperature of 1060°C, estimated using the equation of Tollari et al. (2006; see Section 5.7.8), also corresponds well to the plagioclase solidus at the UZa–UZb boundary.

The estimated liquidus temperature converges to the solidus temperature in the LZc–MZ interval, recording little, if any, subliquidus equilibration. This contrasts to the LZa and LZb below and the UZ above (Fig. 39). This is probably related to the low-trapped melt content in the LZc–MZ interval as discussed in Section 5.7.6. The ‘dome’ in the near solidus estimates is also reflected in the mostly subsolidus equilibration and oxidation temperatures for coexisting magnetite-ilmenite pairs. The FeTi oxides, magnetite and ilmenite, first appear in LZc as early primocrysts at c. 1100°C. Temperatures obtained for coexisting ilmenite and magnetite (Ghiorso & Evans 2008) are at least 200–300°C below the experimental crystallisation temperatures obtained by Thy & Lofgren (1994) for ferrobasaltic melts, and are well into the subsolidus range several hundreds of degrees below magmatic conditions (Fig. 39).

Several observations from Fig. 39 are not easily explained. Low temperatures in the LZ and UZ for the mafic minerals, compared to the higher values for plagioclase, may be related to the presence of high amounts of trapped melt (see Sections 5.11.4 and 5.12.6). This is the “trapped melt effect” suggested by Barnes (1986) to be the result of modification of mafic mineral compositions from reactions with or crystallisation from trapped interstitial melt. The mafic minerals, like olivine, are far more susceptible to diffusional adjustment than plagioclase, which may not be affected within the likely time scales of processes acting in a magma chamber, such as the cooling in the Skaergaard intrusion (Morse 1984; Grove et al. 1984). This is certainly the case for the pyroxenes where solidus and subsolidus re-equilibration and exsolution (see Sections 4.3.3–4.3.5) may have reset mineral compositions and thus the obtained temperatures. Likewise, the effects of the onset of liquid immiscibility in the upper part of the intrusion (UZb; see Section 5.12) may also have affected the pyroxene equilibria (bustamite and ferrohedenbergite in UZc) and the estimated crystallisation temperatures.

5.2 Oxygen fugacity (fO₂)

The temperature and fO₂ constraints during crystallisation and solidification of the Skaergaard intrusion are, and have been, a subject of some contention. The most common approach to constraining fO₂ for evolved gabbroic rocks is the magnetite-ilmenite oxy-geothermometer (Buddington & Lindsley 1964). We employ this approach using the calibration of Ghiorso & Evans (2008) with the understanding that fO₂ estimates reflect conditions at magnetite-ilmenite closure temperatures and not necessarily the liquidus. These results are summarised in Table 9 and illustrated in Fig. 40. The highest temperature determinations cluster around the NNO oxygen buffer at 800–850°C (Fig. 41). Below about 700°C, the variation clusters around the FMQ oxygen buffer to very low temperatures of 400°C or below (Table 9; Figs 40, 41). These temperature estimates are well below any reasonable estimates for the liquidus appearance of coexisting ilmenite and magnetite in the Skaergaard intrusion (Thy & Lofgren 1994; Toplis & Carroll 1996; Thy et al. 2006) and those implied by the thermometry of the coexisting silicates (Fig. 39). Similar results were obtained by Bollingberg (1995) using an extensive, but different sampling of gabbros through the LS. Low temperature determinations for coexisting FeTi oxides have been related to subsolidus oxidation of ulvöspinel to ilmenite and its granule exsolution coarsening as secondary ilmenite (Vincent 1960; Buddington & Lindsley 1964).

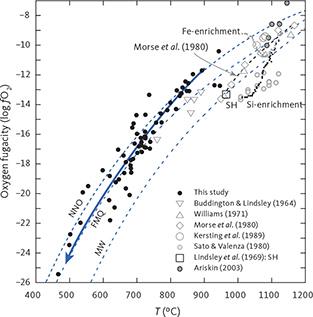
Fig. 40 Summary of subsolidus oxygen fugacity (log fO₂) vs. temperature (T) for coexisting magnetite and ilmenite using the thermobarometer of Ghiorso & Evans (2008). The results of this study (black dots; Table 9) are compared to similar results of Buddington & Lindsley (1964; open inverted triangles) and to selected oxygen buffers (NNO, FMQ and MW). The subsolidus results are compared to various calculated and measured estimates (see Section 5.2 for details). The large blue arrow is a visual interpretation of the overall observed variation. The Morse et al. (1980) trend line is based on a combination of mineral observations and thermodynamic calculations. The Si-enrichment trend line (small black dots) is from Supplementary Table S1, and the Fe-enrichment trend line (small grey dots) is from Supplementary Table S2. Note that the results of Williams (1971) extend to 1300°C but are truncated here.

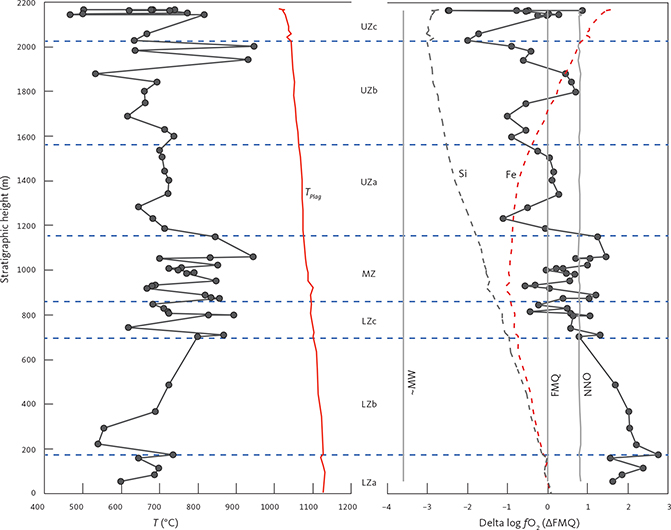
Fig. 41 Subsolidus temperature (T, °C) and oxygen fugacity (fO₂) as a function of stratigraphic height (m). fO₂ is on a log basis normalised to FMQ (ΔFMQ) and calculated from the analysed coexisting magnetite and ilmenite. T_Plag: Liquidus T, calculated based on plagioclase anorthite content. ~MW, FMQ and NNO: oxygen buffers, given for comparison. The MW buffer is schematic and does not show the large fluctuation on the log curve attributable to the T_Plag variation. Si: Si enrichment of the liquid line of descent (Table 21). Fe: Fe enrichment of the liquid line of descent (Table 22). Blue horizontal dashed lines: divisions of the LS. Abbreviations in Fig. 2.

Reconstruction of the primary equilibrium oxide compositions has been an integral process for estimates of temperature and fO₂. Buddington & Lindsley (1964) used the bulk compositions of separated magnetite and ilmenite from the LS (Vincent & Phillips 1954) to approximate the primary compositions. The temperatures obtained by Buddington & Lindsley (1964), varying from 900°C to 775°C and clustering around the FMQ oxygen buffer (Fig. 40), were nevertheless interpreted to reflect subsolidus oxidation with an intergranular fluid action and not late-stage magmatic melts. Further reconstruction was thus required to identify the liquidus conditions. This was attempted by Buddington & Lindsley (1964) and Lindsley et al. (1969) by incorporating granule “oxy-exsolved” ilmenite (Vincent & Phillips 1954; Wright 1961) back into the observed magnetite. The results suggested temperatures from 1150°C to 1025°C for the LZc and 980–950°C for the SH with a corresponding variation in fO₂ from the FMQ to the MW oxygen buffers. Few, if any, of these reconstructed compositions provide information on the primary liquidus conditions. The approach taken in this study has been to analyse the oxide phases with a broad beam or scanning electron beam. This approach does not improve the results, but it allows us to explore the stratigraphic sequence outside the main primary precipitation of ilmenite and magnetite in the LZc and MZ (Fig. 40).

The fO₂ is recorded by both the coexisting oxides and in some coexisting silicates (Frost et al. 1988; Lindsley et al. 1990; Andersen et al. 1993), allowing the uncertainty associated with the coexisting FeTi oxides to be reduced. This approach has been used to further constrain estimates of fO₂ for the Skaergaard intrusion based on the mineralogical data of Wager & Brown (1967), FeTi oxides and silicate equilibria, and independent evaluations of temperature (e.g. Kudo & Weil 1970). Lindsley et al. (1969) calculated the fO₂ –T conditions for the SH using ilmenite-magnetite and fayalite-magnetite-quartz equilibria. Williams (1971) and Morse et al. (1980) obtained results largely consistent with the reconstructed magnetite-ilmenite thermometry by Buddington & Lindsley (1964). The results by Morse et al. (1980) provided internally consistent results that fit the terminal conditions of Lindsley et al. (1969). These latter results have provided the benchmark fO₂ –T variation for the Skaergaard intrusion used by most workers as shown in Fig. 40, from an initial (LZc) fO₂ near the FMQ oxygen buffer, followed by more reducing conditions reaching the MW oxygen buffer at the SH.

Direct measurements of the intrinsic fO₂ of Skaergaard gabbros and mineral separates were made by Sato & Valenza (1980) and Kersting et al. (1989) using the oxygen-specific, solid-electrolyte cell method. This method provides linear relationships between the experimental measurements for temperature and fO₂ and thus still requires an assumption or independent knowledge of the target temperature. Sato & Valenza (1980) examined a suite of magnetically separated FeTi oxides representing the zones and subzones of the LS (McBirney 1989a). Their results plot at reduced conditions between the MW and iron-wüstite (IW) oxygen buffers and temperatures of 1130–1000°C (Fig. 40). They attribute this to the presence of graphite during crystallisation and the fO₂ control of the C-(CO+CO₂) equilibrium, which for an appropriate pressure could explain the observed reduced fO₂ (Sato & Valenza 1980). In a similar study, Kersting et al. (1989) used magnetically separated FeTi oxide mineral concentrates of three gabbros from the collection of Wager & Brown (1967). The result was consistently at about 0.5 log units above the NNO oxygen buffer for oxidising and reducing temperature directions and after argon purging. Furthermore, when they examined the final products using FeTi oxide compositions and Buddington & Lindsley’s (1964) thermobarometer, they obtained fO₂–T relations consistent with their experimental end conditions about one log unit below the electrochemical results between the NNO and FMQ oxygen buffers. These latter results were their preferred values and are also those shown in Fig. 40. The large differences between the two sets of intrinsic fO₂ measurements have been attributed to carbon from the original minerals or carbon introduced during laboratory handling and procedures (Kersting et al. 1989); however, the issue has never been convincingly settled.

Melting experiments used to support modelling of the Skaergaard liquid lines of decent at atmospheric pressure have been conducted in equilibrium with an fO₂ between the IW and NNO oxygen buffers and at temperatures from liquidus to near solidus conditions (Biggar 1974; Hoover 1989a; Snyder et al. 1993; Toplis & Carroll 1995; Thy et al. 2006). The initial crystallisation conditions for the Skaergaard intrusion used for these various experiments varied from 1170°C to –9.5 log fO₂ (Hoover 1989a), 1180°C to –11.6 log fO₂ (Snyder et al. 1993) and 1160°C to –9.4 log fO₂ (Toplis & Carroll 1995, 1996). These estimates range from below the FMQ to well below the MW oxygen buffers and are assumptions often based on Morse et al. (1980) and thus do not represent independent values.

Forward modelling using a preferred initial composition and fO₂ can nevertheless be used to explore the trajectories for temperature and fO₂ of the liquid line of descent assuming various crystallisation models. Toplis & Carroll (1996) modelled the liquid lines of decent for equilibrium and fractional crystallisation for systems open or closed to the exchange of oxygen with the host gabbros of the intrusion. In systems controlled by fractional crystallisation and open to exchange of oxygen, the modelled fO₂ varied parallel to an oxygen buffer defined by the initial conditions, as observed in oceanic volcanic centres. In systems closed to oxygen exchange, as in plutonic centres like the Skaergaard, the modelled fO₂ varied depending on the type of crystallising minerals and their proportions. The modelling that best fitted the observed cumulus sequence of the intrusion was inferred to be fractional crystallisation under conditions closed with respect to the exchange of oxygen with the surroundings (Toplis & Carroll 1996; Thy et al. 2006).

Thy et al. (2006, 2009a) explored the effects of the modes of magnetite and ilmenite. They pointed out that the models that assumed an extrapolation of the experimental modes of FeTi oxides would result in dramatically different trajectories of fO₂ –T than those using the observed mode of the Skaergaard cumulates. The two contrasting trajectories are shown in Fig. 40 marked as either ‘Si enrichment’ (experimental mode; Toplis & Carroll 1996) or ‘Fe enrichment’ (observed modes; Thy et al. 2009a) controlled by the amounts of FeTi oxides used in the calculations. Both paths are generally consistent with the observed mineral-zone layering, although they indicate dramatically different end-stage melt compositions (see Section 5.4). Further, Fig. 41 illustrates the two trajectories expressed as fO₂ on a log basis normalised to FMQ (ΔFMQ) with stratigraphic height. The Si enrichment trend follows the results obtained for the coexisting ilmenite and magnetite, while the Fe enrichment trend is discordant to the observed variation above MZ.

5.3 Lithostatic pressure

The Skaergaard magma chamber intruded into the unconformity between the Precambrian basement and the overlying Tertiary basalts during the peak of continental rifting and build-up of the plateau lava shield (Irvine 1991; Nielsen 2004). The intrusion is interpreted to have intruded around 56–55 Ma, or slightly earlier, after eruption of about half of the plateau lavas, and to have cooled relatively quickly until the overburden thickness had reached its maximum extent 5–6 km (Hirschmann et al. 1997; Barfod et al. 2003; Tegner et al. 2008; Brooks 2011). Holness et al. (2015) suggested that the intrusion originated as a HZ sill composed of several crystal-laden influxes that quickly ballooned to its present volume in response to tectonic expansion.

The pressure at the level of the SH was estimated by Lindsley et al. (1969) at 60 ± 10 MPa using the hedenbergite-bustamite and tridymite-quartz inversions. By assuming a fast inflation of the chamber (Holness et al. 2015) and consequently a constant overburden, the pressure at the level of the LZa can be estimated at 125–130 MPa, using a standard lithospheric gradient of 30 MPa km^–1 (Morse 2008a; Thy et al. 2009b). The effects of such modest anhydrous pressures in the range to 130 MPa will have small or undetectable effects on phase compositions and equilibria, mainly as a modest expansion of the calcic pyroxene field at the expense of plagioclase (Yang et al. 1996; Whitaker et al. 2007; Botcharnikov et al. 2008). This observation justifies the use of one-atmosphere phase equilibria as a reasonable proxy for understanding the main features of the evolution the Skaergaard intrusion (Toplis & Carroll 1995; Thy et al. 2006).

Larsen & Tegner (2006) estimated pressure by using the intercepts between isochoric fluid inclusion paths for granophyre with the minimum melt solidus for granitic compositions. Their results suggested granophyre formation from 180 ± 50 to 330 ± 130 MPa and corresponding temperatures of 690–660°C. They attributed this upward increase in pressure to progressive burial by outpouring of a 5–6 km thick pile of flood basalts during the final stages of cooling following the emplacement of the intrusion as a sub-volcanic chamber.

5.4 End-stage melt compositions

Constraining the end-stage melt composition is an important prerequisite for understanding the dominant differentiation processes in basaltic magma systems as well as for the foundation and confirmation of liquid line of descent modelling.

One line of evidence that may have bearings on the end-melt composition of the Skaergaard intrusion is the occurrences of potential late-stage segregated differentiation products (gabbroic to melanocratic or leucocratic granophyres). In the Skaergaard intrusion, podiform segregation bodies ranging from gabbroic to granophyric (or rhyolitic) in composition are regarded as contemporaneous melt and their evolution believed to approximate to the possible hydrated liquid line of descent of the intrusion (Larsen & Brooks 1994). These granophyric compositions show similarities to observed or theoretically predicted end-stage melts from extreme differentiated basalts or melts formed from initial partial melting of basaltic rocks (Bowen 1928; Tuttle & Bowen 1958; Carmichael 1964; Presnall & Bateman 1973; Beard & Lofgren 1989; Thy et al. 1990; Ghiorso & Carmichael 1995; Villiger et al. 2004).

The granophyric compositions, in addition to showing similarities to predicted end-stage fractional crystallisation melts, also show similarities to the conjugate silicic melt produced as a result of liquid immiscibility in basaltic systems and the Skaergaard magma (McBirney & Nakamura 1974; McBirney 1975; Dixon & Rutherford 1979; Philpotts 1979, 1982; Jakobsen et al. 2005, 2011; Charlier & Grove 2012; Charlier et al. 2013; Honour et al. 2019a). Although it may not be a simple exercise to distinguish between the two types of possible final silicic melts (fractional crystallisation or liquid immiscibility), the presence of a coexisting iron-rich melt or rock, identified either microscopically or macroscopically, is conclusive evidence for action of liquid immiscible melts; although not necessarily of the magnitude of such an effect.

The abundant interstitial granophyric patches in ferrodiorites of the UZc are good candidates for potential end-stage melt compositions originated from liquid immiscibility (Figs 13, 14). Salmonsen & Tegner (2013) reported a granophyre representative for the SH, supporting the contention that granophyre is a final, or one of the final, differentiation products, of the intrusion. Granophyre further commonly appears as veins and dyke and sill-like intrusions throughout the LS, particularly in the UZ and the adjacent UBS, and is commonly viewed as a late-stage, sometimes water-saturated, segregation or columnar migration from the gabbro mush during compaction or other stress-induced movements (Wager & Deer 1939; Wager & Brown 1967; McBirney 1989a; Larsen et al. 1992; Larsen & Brooks 1994; Larsen & Tegner 2006; Jakobsen et al. 2011).

Because of their appearance, granophyric veins and inclusions were not directly sampled and analysed in this study. Although some UZ ferrodoritic samples evidently contain a high amount of interstitial felsic granophyric components localised in the uppermost part of UZc (Figs 13, 14), where quartz reaches c. 10% by weight (Figs 3, 15) or equivalently c. 20% calculated as granophyre (see Sections 5.11.4 and 5.12.6 on trapped melt content). Analyses of granophyres in the LS are provided by Wager & Deer (1939) and McBirney (1989a). In addition to the interstitial granophyre in the gabbros, intrusive and segregated granophyres also exist both in the Skaergaard intrusion and the surrounding host volcanic rocks. These have been referred to as transgressive granophyre dykes (Wager & Brown 1967; Bird et al. 1986; Hirschmann 1992) or as major sills, most noticeably the Tinden and Sydtoppen granophyres (Wager & Brown 1967).

Despite its stratigraphic setting and petrographic integration into the gabbroic or dioritic rocks of the intrusion, granophyre is not always considered the final fractionation product of the Skaergaard magma. The transgressive granophyre dykes are, in particular, interpreted as derived from a Skaergaard-like basaltic magma that incorporated fused Archean crust (Taylor & Forester 1979; Hirschmann 1992). Similarly, Naslund (1989) described from the basaltic Basistoppen sill, which intruded into the Skaergaard, terminal granophyric differentiation products. These were interpreted as resulting from a combination of fractionation of a Skaergaard-like magma and assimilation of melted gneissic host rock. Wager & Deer (1939) further described several granophyric inclusions in the LS and interpreted them as gneissic inclusions. On the other hand, they interpreted the Tinden granophyre and intermediate hedenbergite granophyre of the UZc and SH as representing the final differentiation products.

The assimilation of small amounts of gneiss-derived melts into the evolving Skaergaard magma is well constrained by studies of stable and radiogenic isotopes (Hamilton 1963; Leeman & Dasch 1978; Taylor & Forester 1979; Norton et al. 1984; Stewart & DePaolo 1990; McBirney & Creaser 2003; Hagen-Peter et al. 2019; Cho et al. 2022). More recently, Bindeman et al. (2008) and Wotzlaw et al. (2012) examined ferrodiorites around the SH and concluded that the final magma near the SH became locally reduced in δ¹⁸O due to an influx of meteoric water derived from blocks of altered UBS assimilated during the time of MZ formation. These authors also suggested that the still hot rocks around the SH might have been reheated and partially melted by the emplacement of the thick Basistoppen sill only a few hundred metres above.

A comprehensive study of the granophyres of the intrusion has, however, not been conducted as part of the present study. Nevertheless, the granophyres in the LS range from felsic granophyre to melanocratic granophyre (or melanogranophyre). The melanogranophyres have gained a special status in recent studies having been interpreted as in part recording liquid immiscibility (McBirney & Nakamura 1974; McBirney 1975, 1989a, 1995, 1996; Jakobsen 2007; Jakobsen et al. 2011). However, there is no petrographic or structural field evidence of their origin or their relationships to leucocratic granophyres.

Table 18 summarises existing information available for the compositions of major and trace elements of Skaergaard-related granophyres including granophyre (McBirney 1989a; Larsen & Brooks 1994; Salmonsen & Tegner 2013), melanogranophyre (McBirney 1989a), transgressive granophyre (Hirschmann 1992) and the Basistoppen sill (Naslund 1989). The granophyric rocks contain variable additions of the coexisting primocrysts, reflected by elevated TiO₂, FeO, MgO and CaO particularly for the melanogranophyres (Table 18). The trace elements, however, have received less attention as summarised in Table 18. There is nevertheless a reasonable correspondence between the trace elements, often within an order of magnitude, and the felsic granophyres and the melanogranophyres. Typical included and excluded trace elements ratios approaching the SH, like Ni/Rb, range from 0.06 to 0.15 and 0.14 to 0.22 for V/Rb, although melanogranophyres reach 0.76 in the latter, probably due to inclusion of accidental coexisting primocrysts or from reactions between gabbro and granophyre melts forming hybrid material (Wager & Deer 1939, p. 189). It is thus suggested that granophyre is the only identifiable late-stage silicic component in the Skaergaard.

Table 18 Summary of average Skaergaard granophyric compositions compared to modelled compositions

Oxide (wt%)	Granophyre			Transgressive granophyre			Basistoppen	Melanogranophyre			Sandwich Horizon (SH)			Uzb–UZc Boundary			Ave. granite
	n	Ave.	SD	n	Ave.	SD	Ave. (n = 2)	n	Ave.	SD	Gabbros analysed	Melt (Si) modelled	Melt (Fe) modelled	Gabbros analysed	Melt (Si) modelled	Melt (Fe) modelled
SiO2	19	74.30	3.07	15	69.25	3.57	67.55	7	57.35	3.06	50.17	74.43	55.89	45.64	72.68	55.57	72.04
TiO2	19	0.66	0.32	15	0.46	0.29	0.67	7	2.07	0.38	1.87	0.10	0.92	2.54	0.10	1.03	0.30
Al2O3	19	12.11	0.68	15	14.23	0.80	11.58	7	11.21	0.98	9.40	10.01	5.04	8.98	10.06	5.57	14.42
Fe2O3	10	2.59	0.62	15	1.16	0.42	2.81	4	3.38	1.91	6.28	0.12	8.73	2.68	0.30	8.20	1.22
FeO	10	3.25	2.11	15	2.68	1.85	5.30	4	11.85	0.75	18.45	9.61	21.20	23.96	10.27	21.01	1.68
Fe2O3*	19	5.82	2.75	15	4.14	2.39	8.69	7	15.05	2.91	26.78	10.81	32.30	29.31	11.71	31.55	1.68
MnO	19	0.09	0.04	15	0.07	0.03	0.16	7	0.23	0.05	0.19	0.29	0.30	0.74	0.29	0.31	0.05
MgO	19	0.32	0.30	15	0.53	0.41	2.75	7	1.41	0.48	0.03	0.10	0.40	0.68	0.10	0.40	0.71
CaO	19	1.55	0.84	15	1.87	1.11	4.36	7	4.82	0.96	7.89	1.85	2.00	9.65	2.33	2.00	1.82
Na2O	19	4.38	0.34	15	4.63	0.27	1.87	7	3.84	0.47	3.25	4.08	2.27	2.68	4.03	2.40	3.69
K2O	19	2.97	0.78	15	3.93	0.74	2.87	7	1.76	0.20	0.80	3.28	3.91	0.32	3.12	3.65	4.12
P2O5	19	0.12	0.12	15	0.20	0.30	0.09	7	0.55	0.23	0.36	0.10	0.10	0.71	0.10	0.10	0.12
Total		102.35			99.00		97.13		98.47		98.70	103.98	100.77	98.57	103.38	100.24	100.17
Trace Elements (ppm)												Inverted	Inverted		Inverted	Inverted
Co	13	9	6	12	6	6	2	7	26	4	3	1	3	37	20	45
Sc				12	6	4	8				44	2	3	37	4	8
V	12	10	5	8	19	10	9	3	30	52	24	10	26	6	2	5
Cr	7	7	2	11	9	4	23	5	7	2	22	0.2	1	10	0.1	0.3
Ni	9	10	6	15	5	5	9	5	4	3	4	0.0	0.1	1	0.0	0.0
Zn	19	79	48	15	71	25	253	7	161	70	259	250	630	153	183	417
Rb	22	69	20	15	87	23	65	7	40	7	16	76	147	5	39	83
Sr	23	142	46	15	156	92	173	7	240	35	570	296	354	298	255	359
Y	15	152	34	13	39	63	145	3	128	20	117	79	142	62	40	83
Zr	19	971	308	12	311	95	1275	7	568	175	398	140	361	77	44	179
Nb	6	93	23	12	30	9	90				52	20	51	11	6	14
Cs				12	0.8	0.3
Ba	19	665	196	15	807	208	805	7	473	109	349	462	435	87	1903	1482
La	6	138	51	12	64	9	93	1	51		35	60	121	13	27	61
Ce	6	203	56	12	134	16	201				98	125	245	35	57	126
Nd				12	58	11	99				82	67	125	30	31	66
Sm				12	12	2	28				23	15	26	9	7	14
Eu				12	2	0.9	6				12	7	12	4	3	6
Gd											22	14	24	10	7	15
Dy							26				22	15	26	10	7	15
Ho											4	3	5	2	1	3
Er											11	8	14	6	4	8
Tm											2	1	2	1	0.6	1
Yb				12	5	0.8	14				11	8	13	5	4	7
Lu				12	0.6	0.1	2				2	1	2	1	0.6	1
Hf				12	12	2	29				9	2	7	2	0.5	4
Ta				12	1.4	0.5	4				3	1	3	1	0.4	1
Pb	9	11	3				16	3	19	16	3	7	16	1	5	11
Th	9	12	2	12	9	2	9	3	9	1	2	13	29	1	6	13
U				12	3	0.7	2.7				0.6	3	3	0.2	4	8
Average (Ave.), standard deviation (SD), and number of analyses (n). Fe2O3* is total iron calculated as Fe2O3. Granophyre from McBirney (1989a), Larsen & Brooks (1994), Salmonsen & Tegner (2013) and R.B. Larsen (2016 personal cummunication). Transgressive granophyres from Hirschmann (1992). Basistoppen granophyre from Naslund (1989). Melanogranophyre from McBirney (1989a) and R.B. Larsen (2016 personal communication). Analysed gabbro from Table 13. Modelled major element compositions (inverted) for Si- and Fe-enrichment trends (model Si and model Fe, respectively) from Tables 21 and 22, respectively. Inverted trace element compositions as modelled in this study (Figures 60 and 62). Missing trace element data were not given in the original sources. Standard deviation are calculated for n > 2.

Wager & Deer (1939, p. 112–117) suggested that the final 200 m of rocks of the SH represented a sheet of melt from which initially fayalitic olivine settled to the base and andesitic plagioclase floated to the top. The final solidification of this sheet occurred without fractionation ending up as a fayalite-hedenbergite granophyre, a term that they applied to the major part of the UZc. The central fayalitic-hedenbergitic granophyre of Wager & Deer (1939) and Wager & Brown (1967, p. 95) can be “[..] regarded as a mildly intrusive, penecontemporaneous sheet.” They observed that “[..] there still remains a thin layer of rock, of distinctive composition, which is believed to have formed from residual liquid sandwiched between the upper border group and the LS, and which cannot satisfactorily be classified with either of the adjacent groups.” The primocryst phases in this thin layer were described as andesine plagioclase (An_~30), fayalitic olivine and hedenbergitic pyroxene. Thus, Wager & Brown (1967, p. 95) argued for an iron-rich Skaergaard end product that they referred to as ferrodiorite containing zoned plagioclase, brown ferrohedenbergite, fayalite and iron ore with quartz and orthoclase in abundant (5%) silicic mesostasis areas (e.g. in Fig. 14). Wager & Brown (1967) further interpreted melanogranophyres, granophyres, and some acid granophyres as melts that were segregated from the extreme ferrodioritic fractionation product of the SH or that the mesostasis areas of the ferrodiorites in their view represented the final differential product. McBirney (1975, 1989a) suggested that only melanogranophyres and what he referred to as segregation granophyric veins and sills, both types occurring in the UZc, were true silicic differentiation products from the Skaergaard magma that resulted from liquid immiscibility followed by buoyant separation and accumulation. Despite these early observations, in subsequent papers McBirney did not argue for liquid immiscibility during the evolution of the Skaergaard magma (McBirney 1995, 1996).

Observations by Wager & Brown (1967) and McBirney (1989a), as well as those presented here, suggest that the final melt composition at the SH level was in equilibrium with oligoclase (An_~30), fayalitic olivine and hedenbergite. The interstitial granophyric melt crystallised to form a fine-grained assemblage of quartz, orthoclase and albitic plagioclase (Fig. 14). Although it is possible that the interstitial granophyre could be in equilibrium with fayalite and quartz, there are no strong indications that the granophyre interacted strongly with the primocrysts (Fig. 14) or that fayalite and hedenbergite formed during final crystallisation (Fig. 13). There are, however, some indications that the interstitial granophyre melt may have interacted with the andesine plagioclase in the host to form zoning towards pure albite (Fig. 13) and thus may not have been in equilibrium with oligioclase. A further complication is that the proportion of granophyre increases upwards in the stratigraphy towards the SH, which is difficult to reconcile with the notion that granophyre is the residual melt resulting from extreme fractional crystallisation.

The interpretation advocated here, based on petrographic and compositional evidence, is that the final differentiated product of the Skaergaard intrusion can be represented by two melt compositions: ferrodiorite and granophyre. The ferrodiorites above the UZa–UZb boundary (Table 18), where fractionation appears to have slowed (Fig. 30), represent the basaltic differentiate. These ferrodiorites are made of mixtures of granophyric melt and mafic primocrysts (Fig. 14). The former increases in volume upward in the UZc (Fig. 15) due to melt migration and accumulation of an immiscible silicic melt. The granophyre component thus represents the final silicic differentiation product, but not necessarily the final differentiation product of the host ferrodiorites. There are no strong indications as to whether iron-rich and sodium-rich primocrysts of the ferrodiorites are in equilibrium with the granophyric component. Nor are there any clearly observed primocrysts of quartz, orthoclase and albite – the main components of the interstitial granophyre – in the ferrodiorites, although some reactive interactions between the two components cannot be excluded (see Section 5.12 for further discussion).

5.5 Liquid summation and the liquid line of descent

Weighted mass balance, liquid summations based on the average compositions of the gabbros zones and subzones, have been used to infer the bulk (or parental) magma composition as well as its liquid line of decent. The calculations require knowledge of the corresponding zone proportions of the intrusion, including the LS, UBS and MBS (Nielsen 2004) and average compositions of the respective zone divisions (McBirney 1989a; Hoover 1989b; Nielsen 2004; Salmonsen & Tegner 2013). Although the approaches are similar, the details in the calculations may vary between (1) starting with an initial composition and subsequently subtracting the zone compositions (Andersen 2006; Nielsen et al. 2009) and (2) starting with an end composition, such as a granophyre, and subsequently adding the zone compositions (Hunter & Sparks 1987; Tegner 1997; Tegner & Cawthorn 2010). Furthermore, the modelling often modifies the starting composition by adding a melanogranophyre component (5%; Andersen 2006; Nielsen et al. 2009) or by adding a melanogranophyre component amounting to 15% in the UZc, 5–8% in UZb, and 2% in the remaining LS (e.g. Tegner 1997; Tegner & Cawthorn 2010). Andersen (2006) and Nielsen et al. (2009) used an initial bulk-gabbro composition from Nielsen (2004) that represented the base of the LZa with 5% added melanogranophyre and adjusted to equilibrium with olivine Fo₆₈ and the derived melt at the base of MZ to be quartz-normative. Such adjustments of adding granophyric compositions to the gabbros are equivalent to assuming that the sampled gabbros are not representative of the residual mush and may have lost a component of granophyre (or similar silicic melt), presumably following late-stage liquid immiscibility (see Section 5.12).

Fig. 42A compares the previously calculated liquid lines of decent. Tegner (1997) and Tegner & Cawthorn (2010) observed that iron content of plagioclase increases upwards in the LS and relate this to a corresponding increase in the iron content of melt (cf. Lundgaard & Tegner 2004). Their summation calculation assumes an average ferrodioritic rock composition at the centre of UZc (Tegner 1997). Nielsen et al. (2009) and Andersen (2006) use a melanogranophyre terminal composition, while Hunter & Sparks (1987) assumed a granophyre as the terminal composition (Tinden sill). Wager (1960) and Wager & Brown (1967) used a graphical method based on a HZ basaltic parental composition (EG 4502; Fig. 42A). Their results indicated pronounced iron enrichment with modest silica enrichment into the UZb and well past FeTi oxide appearance (LZc; not shown on Fig. 42A) and resulted in a melanocratic granophyre as the terminal differentiation product. Consequently, their results for the UZ are similar to those of Andersen (2006) and Nielsen et al. (2009).

Fig. 42B shows new summation calculations using the gabbro compositions from Table 13 and three different silicic end compositions from Table 18 (SH ferrodiorite, melanogranophyre and granophyre) shown as model A, B, and C, respectively, without making assumptions about the fate of a granophyric component. Other variables in the calculations include zone proportions after Nielsen (2004) and the bulk-gabbro compositions of the MBS, LS and UBS from Hoover (1989b), McBirney (1989a) and Salmonsen & Tegner (2013). The initial magma estimated for each of these is similar (Table 19). It is noticeable that all the modelled liquid lines of descent show strong iron enrichment without much silica enrichment throughout the LS and into the UZb (Fig. 42B). The appearance of FeTi oxides (LZc) results in a short reversal in iron enrichment that resumes through the MZ and UZa, accompanied by a modest increase in both silica and iron with the latter reaching 23–24 wt% FeO*. Evolution beyond UZa depends on the choice of the granophyric terminal melt (model ‘C’ in Fig. 42B) displaying the most marked decrease in iron and increase in silica (Fig. 42B).

Table 19 Summary of calculated parental melt compositions for the Skaergaard intrusion using the summation method

End-melt gabbro	Granophyre	T & C	Nielsen	Andersen
	(modified a)
Base of:	HZ	LZa	HZ	LZa
SiO2	47.86	47.58	47.90	47.63
TiO2	3.17	3.40	3.09	2.99
Al2O3	14.52	13.55	13.80	13.38
FeO*	14.30	15.78	15.43	15.65
MnO	0.21	0.23	0.24	0.23
MgO	6.57	6.16	6.13	7.10
CaO	10.18	9.95	10.18	9.87
Na2O	2.59	2.63	2.57	2.49
K2O	0.35	0.38	0.40	0.39
P2O5	0.26	0.34	0.28	0.27
Mg#	0.45	0.41	0.41	0.45
a Composition of this study is modified by adding granophyre as 2% for HZ–UZa, 5% for UZb, and 15% for Uzc. Mg#: calculated as Mg/(Mg+Fe) with iron as total Fe. T&C: Tegner & Cawthorn (2010), their table 1. Nielsen: Nielsen (2004), SK-TFDN in their table 3. Andersen: Andersen (2006), their table 3.

The effects of restoring the gabbro compositions to assumed mush compositions (see Section 5.12 for further details), in this case by adding granophyric melt to the gabbro, is also illustrated in Fig. 42B by the lines labelled ×1 and ×2. In the former, it is assumed that granophyre was added to UZa, UZb, and UZb in the proportions 2%, 5% and 15%, respectively. These amounts are similar to the proportions assumed in the model of Tegner & Cawthorn (2010), although the composition of granophyre is different. In the second case (×2), the amounts of granophyre are doubled in each subzone. These trapped mush models show marked differences in the liquid line of descent compared to model C without the added granophyre. This exercise illustrates the sensitivity of the liquid line of descent to assumptions about the amount and distribution of trapped granophyre. We submit that this, together with the composition of residual liquid(s), can account for at least some of the diversity of proposed liquid trends from strong iron enrichment at nearly constant silica-to-iron depletion and strong silica enrichment. Nevertheless, ascribing a unique liquid line of descent for the Skaergaard intrusion based on these considerations alone remains tenuous and highlights a shortcoming of summation models.

5.6 Forward modelling of major oxides

The systematic cryptic variation in mineral compositions from the start of crystallisation to the final stages has been interpreted to reflect magma differentiation in a closed, or essentially closed, chamber (Wager & Deer 1939; Wager & Brown 1967). The essential mechanisms controlling the differentiation are widely accepted as one of solid-liquid fractional crystallisation resulting from an accumulation of mineral components on the base and walls of the chamber and the return of melt to a mainly convective and homogenised magma chamber (Maaløe 1976b; McBirney 1995, 1996; Tegner et al. 2009).

Attempts to model perfect fractional crystallisation for the Skaergaard intrusion have been made using forward modelling approaches constrained by relevant experimental phase equilibria (e.g. Toplis & Carroll 1995, 1996; Thy et al. 2006, 2008, 2009a). The success of such forward modelling is measured by its ability to predict essential features of the observed mineral assemblage and cryptic mineral variations, and thereby the composition of the coexisting melts. The summation method (see Section 5.5) complements the forward modelling by estimating the liquid line of descent and initial melt composition (Fig. 42) using information on the composition of the gabbro zones and subzones in addition to assumptions of the initial or end-stage melt compositions (see Section 5.4).

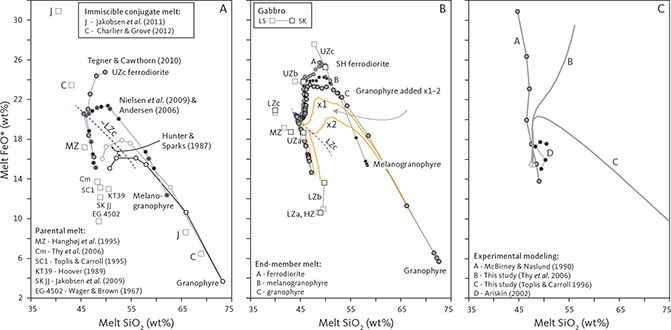
Fig. 42 Calculations of the liquid line of descent and initial melt composition shown on FeO* vs. SiO₂ binary diagrams (wt%). A: Classic studies by Hunter & Sparks (1987), Andersen (2006), Nielsen et al. (2009) and Tegner & Cawthorn (2010). Although the calculations assume or result in three different end-melt compositions (granophyre, melanogranophyre and UZc ferrodiorites), they also assume or result in approximately similar parental melt compositions for LZa and HZ (see Table 19). The calculations by Wager (1960) and Wager & Brown (1967) assume an initial melt composition with much lower initial FeO* (EG 4502), but still suggest a liquid line of descent (not shown on diagram) similar to that of Nielsen et al. (2009) and Andersen (2006). Various parental melt compositions, as also suggested, are shown together with the immiscible conjugate melts found by Jakobsen et al. (2005, 2011) and Charlier & Grove (2012). B: Summation calculations based on the present LS gabbro compositions (Table 13) and end-melt compositions (Table 18). The three main liquid lines of descent using different end-melt modelling are: ferrodiorite, melanogranophyre and granophyre. The bulk-gabbro zone compositions are shown for comparison for both LS and the bulk intrusion (SK). The effects of adding granophyre are illustrated (orange curves): The curve marked ×1 uses the equivalent granophyre proportions of Tegner & Cawthorn (2010) and the curve marked ×2 uses double these proportions. C: Experimental and forward experimental modelling. Data shown include the melting results of McBirney & Naslund (1990), the two end-member liquid line of descent based on Toplis & Carroll 1996, Thy et al. (2006), Tables S1 and S2 and the modelling of Ariskin (2002).

5.6.1 Crystallisation conditions and parental melt compositions

The forward modelling hinges on the identification of parental melt compositions for the magma chamber and the acceptance of crystallisation conditions. The initial fO₂ for the Skaergaard magma is believed to be close to the FMQ oxygen buffer (Morse et al. 1980; Toplis & Carroll 1995; Thy et al. 2006; see Section 5.2). But the parental magma composition remains uncertain (Table 20). Early attempts to constrain this focused on chilled margins of the intrusion (Wager 1960, 1961; Biggar 1974; McBirney 1975; Naslund 1984; Hoover 1989a) and later on an associated dyke swam (Brooks & Nielsen 1978, 1990; Nielsen 1978; Toplis & Carroll 1995, 1996; Thy et al. 2006; Jakobsen et al. 2010). Examinations of melt inclusions in plagioclase have also suggested primary melt composition at the MZ level (Hanghøj et al. 1995; Jakobsen et al. 2010). The study by Jakobsen et al. (2010) on melt inclusions in troctolite inclusions in a Skaergaard dyke suggested primary melt compositions with significantly higher Mg# than those suggested by the associated dyke compositions and summation calculations (Fig. 42B). More recent work has tried to identify units of the contemporaneous East Greenland Plateau flood basalts as likely sources for the initial Skaergaard magma (Andreasen et al. 2004; Nielsen 2004; Nielsen et al. 2019a; Cho et al. 2022).

Table 20 Suggested initial melt compositions for the Skaergaard intrusion (wt%)

	EG4507	KT39	SC1	Cm	Nielsen 04	SK JJ
SiO2	48.52	50.35	48.75	47.72	47.99	48.82
TiO2	1.18	2.65	2.90	2.88	3.04	2.24
Al2O3	17.38	13.47	14.89	13.76	13.90	14.42
FeO*	9.71	13.46	13.09	15.27	15.13	12.13
MnO	0.16	0.20		0.25	0.22	0.18
MgO	8.70	6.57	6.49	6.34	6.30	6.06
CaO	11.48	10.15	10.89	10.64	10.18	12.57
Na2O	2.39	2.43	2.70	2.46	2.57	3.01
K2O	0.25	0.57	0.30	0.42	0.40	0.38
P2O5	0.22	0.15		0.26	0.27	0.20
Mg#	0.614	0.465	0.469	0.425	0.426	0.51
Normalised anhydrous to 100% and with all iron as FeO. Mg#: Mg/(Mg+Fetotal). EG4507: Wager (1960). KT39: Hoover (1989b). SC1: Toplis & Carroll (1995) prepared without MnO and P2O5. Cm: composition used in this study based on Brooks & Nielsen (1978, 1990). Nielsen 04: Nielsen (2004). SK JJ: Jakobsen et al. (2010).

 

Table 21 Modelled silica enrichment melt compositions

Zone	Stratigraphic height (m)		F	T (°C)	logfO2	SiO2	TiO2	Al2O3	Fe2O3	FeO	FeO*	MnO	MgO	CaO	Na2O	K2O	P2O5	Total	Pl	Ol	Pyroxene (Mg#)
	high	low				(wt%)	(wt%)	(wt%)	(wt%)	(wt%)	(wt%)	(wt%)	(wt%)	(wt%)	(wt%)	(wt%)	(wt%)	(wt%)	(An)	(Fo)
UBS	2169	2165	0.00	1012	–13.5	74.48	0.10	10.01	0.12	9.59	9.70	0.29	0.10	1.83	4.08	3.29	0.10	103.99	0.019	0.000	0.000
UZc	2165	2165	0.00	1020	–13.5	74.43	0.10	10.01	0.12	9.61	9.72	0.29	0.10	1.85	4.08	3.28	0.10	103.98	0.020	0.000	0.000
UZc	2165	2164	0.00	1025	–13.5	74.43	0.10	10.01	0.12	9.61	9.72	0.29	0.10	1.85	4.08	3.28	0.10	103.98	0.020	0.000	0.000
UZc	2163	2147	0.00	1021	–13.5	74.40	0.10	10.01	0.13	9.62	9.74	0.29	0.10	1.85	4.08	3.28	0.10	103.97	0.021	0.000	0.000
UZc	2144	2141	0.00	1027	–13.5	74.15	0.10	10.02	0.15	9.72	9.86	0.29	0.10	1.93	4.07	3.26	0.10	103.88	0.026	0.000	0.000
UZc	2091	2081	0.01	1037	–13.4	73.39	0.10	10.04	0.23	10.00	10.21	0.29	0.10	2.13	4.05	3.19	0.10	103.62	0.042	0.000	0.000
UZc	2075	2060	0.01	1036	–13.4	73.16	0.10	10.05	0.25	10.09	10.32	0.29	0.10	2.20	4.04	3.16	0.10	103.54	0.047	0.000	0.000
UZc	2060	2046	0.01	1042	–13.4	72.93	0.10	10.05	0.28	10.18	10.42	0.29	0.10	2.26	4.04	3.14	0.10	103.46	0.052	0.000	0.000
UZb	2044	2030	0.02	1031	–13.4	72.68	0.10	10.06	0.30	10.27	10.54	0.29	0.10	2.33	4.03	3.12	0.10	103.38	0.057	0.000	0.000
UZb	2024	1984	0.02	1043	–13.3	72.37	0.10	10.07	0.33	10.38	10.68	0.29	0.10	2.41	4.02	3.09	0.10	103.27	0.064	0.000	0.000
UZb	1962	1921	0.03	1045	–13.2	71.35	0.10	10.10	0.44	10.76	11.15	0.29	0.10	2.69	3.99	2.99	0.10	102.91	0.085	0.000	0.000
UZb	1902	1862	0.04	1047	–13.2	70.31	0.10	10.12	0.54	11.14	11.63	0.29	0.10	2.98	3.96	2.90	0.10	102.55	0.107	0.000	0.000
UZb	1843	1801	0.05	1052	–13.1	69.24	0.10	10.15	0.65	11.54	12.12	0.29	0.10	3.27	3.93	2.79	0.10	102.16	0.129	0.000	0.000
UZb	1782	1748	0.06	1050	–13.0	68.09	0.10	10.18	0.77	11.95	12.65	0.30	0.10	3.58	3.89	2.69	0.10	101.75	0.152	0.000	0.000
UZb	1728	1691	0.07	1055	–12.9	67.05	0.10	10.21	0.88	12.32	13.12	0.30	0.10	3.87	3.85	2.59	0.10	101.37	0.172	0.000	0.000
UZb	1671	1630	0.09	1055	–12.8	65.93	0.10	10.23	1.00	12.72	13.62	0.30	0.10	4.17	3.82	2.48	0.10	100.96	0.194	0.000	0.000
UZb	1620	1600	0.10	1060	–12.7	64.92	0.10	10.25	1.11	13.08	14.08	0.30	0.10	4.45	3.78	2.39	0.30	100.78	0.214	0.000	0.000
UZa	1561	1527	0.11	1063	–12.6	63.73	0.10	10.28	1.23	13.49	14.60	0.30	0.10	4.77	3.74	2.28	2.00	102.02	0.237	0.000	0.000
UZa	1506	1431	0.13	1067	–12.5	62.62	0.10	10.30	1.35	13.88	15.09	0.30	0.10	5.08	3.70	2.17	1.87	101.46	0.258	0.000	0.013
UZa	1403	1343	0.15	1072	–12.2	60.54	0.17	10.34	1.58	14.57	15.99	0.31	0.10	5.64	3.62	1.97	1.63	100.12	0.297	0.039	0.120
UZa	1323	1282	0.18	1072	–12.1	58.96	0.39	10.37	1.75	15.09	16.66	0.31	0.26	6.07	3.55	1.82	1.46	100.00	0.326	0.087	0.199
UZa	1268	1237	0.19	1073	–11.9	57.90	0.76	10.39	1.87	15.42	17.10	0.31	0.42	6.36	3.50	1.72	1.35	100.00	0.345	0.120	0.250
UZa	1218	1188	0.21	1074	–11.8	56.97	1.09	10.40	1.97	15.70	17.48	0.31	0.58	6.62	3.46	1.63	1.26	100.00	0.362	0.149	0.294
UZa	1178	1131	0.22	1075	–11.7	56.22	1.35	10.41	2.06	15.92	17.78	0.31	0.71	6.82	3.42	1.56	1.18	100.00	0.375	0.173	0.327
MZ	1098	1055	0.25	1077	–11.5	54.83	1.84	10.44	2.22	16.32	18.32	0.31	0.98	7.20	3.35	1.42	1.05	100.00	0.400	0.219	0.389
MZ	1053	1032	0.27	1081	–11.4	54.08	2.10	10.45	2.30	16.52	18.60	0.32	1.14	7.41	3.31	1.35	0.98	100.00	0.414	0.245	0.421
MZ	1024	1009	0.28	1083	–11.3	53.61	2.27	10.45	2.36	16.64	18.76	0.32	1.25	7.54	3.29	1.31	0.94	100.00	0.423	0.261	0.441
MZ	1003	1002	0.29	1085	–11.3	53.28	2.38	10.46	2.39	16.73	18.88	0.32	1.32	7.63	3.27	1.27	0.92	100.00	0.429	0.272	0.455
MZ	988	961	0.29	1088	–11.2	53.05	2.46	10.46	2.42	16.78	18.96	0.32	1.38	7.69	3.25	1.25	0.90	100.00	0.433	0.281	0.464
MZ	953	930	0.30	1087	–11.2	52.53	2.64	10.47	2.48	16.90	19.14	0.32	1.51	7.84	3.22	1.20	0.85	100.00	0.443	0.300	0.485
MZ	921	900	0.32	1099	–11.1	52.07	2.80	10.48	2.54	17.00	19.29	0.32	1.63	7.97	3.19	1.15	0.82	100.00	0.451	0.317	0.503
MZ	890	875	0.33	1093	–11.0	51.65	2.95	10.48	2.59	17.09	19.42	0.32	1.75	8.09	3.16	1.11	0.78	99.99	0.460	0.333	0.520
LZc	847	816	0.35	1095	–10.9	51.09	3.15	10.49	2.65	17.20	19.58	0.32	1.92	8.25	3.12	1.05	0.74	99.99	0.471	0.355	0.541
LZc	808	798	0.36	1093	–10.8	50.62	3.31	10.50	2.71	17.27	19.71	0.32	2.08	8.38	3.08	1.01	0.70	99.99	0.480	0.374	0.559
LZc	784	742	0.37	1096	–10.7	50.34	3.40	10.51	2.74	17.31	19.78	0.32	2.18	8.46	3.06	0.98	0.68	99.99	0.486	0.386	0.569
LZc	723	703	0.40	1103	–10.6	49.70	3.62	10.53	2.82	17.38	19.92	0.32	2.43	8.65	3.00	0.91	0.64	99.99	0.501	0.415	0.593
LZb	703	681	0.41	1099	–10.5	49.51	3.68	10.54	2.85	17.39	19.95	0.32	2.51	8.71	2.99	0.89	0.62	99.99	0.506	0.424	0.600
LZb	634	580	0.44	1108	–10.3	48.91	3.88	10.57	2.92	17.40	20.02	0.32	2.81	8.89	2.92	0.82	0.58	99.98	0.521	0.455	0.622
LZb	558	488	0.47	1110	–10.2	48.38	4.05	10.61	2.98	17.34	20.02	0.32	3.13	9.07	2.86	0.76	0.54	99.98	0.538	0.487	0.642
LZb	447	367	0.53	1113	–9.9	47.82	4.19	10.69	3.04	17.13	19.87	0.32	3.61	9.28	2.76	0.69	0.50	99.97	0.563	0.529	0.667
LZb	346	221	0.58	1121	–9.7	47.54	4.23	10.80	3.06	16.82	19.58	0.31	4.05	9.44	2.68	0.64	0.46	99.96	0.585	0.564	0.685
LZb	177	173	0.67	1126	–9.3	47.46	4.10	11.08	3.00	16.09	18.79	0.30	4.75	9.66	2.56	0.59	0.41	99.95	0.622	0.615	0.714
LZa	161	137	0.68	1119	–9.3	47.47	4.08	11.12	2.99	16.01	18.70	0.30	4.82	9.68	2.55	0.59	0.40	99.94	0.626	0.619	0.716
LZa	125	107	0.70	1126	–9.3	47.51	4.02	11.21	2.97	15.82	18.49	0.30	4.96	9.72	2.53	0.58	0.39	99.94	0.634	0.629	0.722
LZa	96	27	0.71	1131	–9.2	47.54	3.96	11.29	2.94	15.66	18.31	0.30	5.07	9.76	2.52	0.58	0.38	99.93	0.641	0.636	0.727
LZa	7	0	0.76	1126	–9.1	47.67	3.77	11.57	2.84	15.16	17.72	0.29	5.39	9.90	2.48	0.56	0.34	99.92	0.660	0.657	0.744
F=1	–365		1.00	1163	–9.0	47.22	2.82	13.80	2.09	13.35	15.23	0.24	6.26	11.24	2.47	0.34	0.30	99.92	0.695	0.733	0.780
Melt composition calculated from the silica-enrichment forward modeling by Thy et al. (2006) and reasonable values for P2O5 in UZc. FeO*: total iron as FeO. The modelled TiO2 and MgO becomes negative at F ~ 0.13 in the upper part of UZa and were fixed at small positive values for the rest of the stratigraphy. T is calculated from plagioclase An (mol%) content based on Thy et al. (2009b, 2013). F: fraction of melt remaining. Values in italic are assumed. See the Supplementary File S3 for complete modeling results. An and Fo as mole fractions.

A summary of initial Skaergaard magmas can be found in Table 20. The original chilled margin composition (EG4507) suggested by Wager (1960) was used by Biggar (1974) for a one-atmosphere study of the effects of fO₂ and temperature on phase equilibria. The chilled margin composition ‘KT39’ was used for low-pressure experimental work by Hoover (1989a) and Snyder et al. (1993) to study the effects of fO₂ and temperature. The composition ‘Cm’ that represents the chilled margin composition of an associated dyke is very similar to the bulk Skaergaard intrusion calculated by Nielsen (2004) and obtained in this study using the summation technique (see Section 5.5 and Table 19). The latter is the initial Skaergaard composition used for the forward modelling of Toplis & Carroll (1995) and Thy et al. (2006).

5.6.2 Experimental foundation

Our forward modelling relies on one-atmosphere melting experiments from liquidus to near solidus conditions using a set of Skaergaard-related chilled dyke margins (Brooks & Nielsen 1978, 1990). The experimental methods, results and forward modelling procedures were presented by Thy et al. (2006) and further developed by Thy et al. (2009a). Here, we only summarise the main experimental results and modelling approach relevant to the present discussion.

A total of four olivine and hypersthene CIPW normative compositions of dyke margins were used, with Mg/(Mg+Fe^total) = 0.51–0.41, CaO/Al₂O₃ = 0.83–0.74 and TiO₂ = 2.05–4.36 wt%. These compositions are typical of ferrobasalts occurring within the coeval East Greenland plateau lavas (Brooks & Nielsen 1978; Larsen et al. 1989; Pedersen et al. 1997; Tegner et al. 1998; Andreasen et al. 2004; Nielsen et al. 2019a) and the rift zones of Iceland (e.g. Thy 1983, 1989). They are thus plausible candidates for the initial melt composition for the Skaergaard intrusion.

Equilibrium melting experiments were conducted at the FMQ oxygen buffer using a CO-CO₂ gas mixture. The melting temperatures ranged from the liquidus at 1182–1154°C to the near solidus at 1078–1089°C and produced olivine, plagioclase, augite, ilmenite, magnetite and pigeonite coexisting with melts of Mg/(Mg+Fe^total) down to 0.26–0.22 and with maximum TiO₂ contents of 4.53–5.20 wt%. Cumulative modes are illustrated in Fig. 43. Plagioclase (An_73-60) and olivine (Fo_77-70) are on the liquidus at high temperature with almost all liquid remaining (F ≈ 1.0), followed by augite (Mg# 77–70) on the liquidus at F = 0.90 and coexisting ilmenite and magnetite at F = 0.35. Pigeonite replaces olivine for some experiments at F = 0.30 after the appearance of FeTi oxides. The modal variations as a function of F form the basis for our forward modelling of the liquid lines of decent (Fig. 43), with the extrapolated low F values.

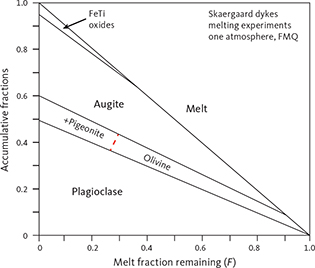
Fig. 43 Summary of the one-atmosphere melting experiments on Skaergaard-related dykes of Thy et al. (2006) shown as the accumulative mineral fractions vs. melt fraction remaining (F). Short red dashed line: approximate transition from olivine to pigeonite.

5.6.3 Fractional crystallisation model

The modal variation shown in Fig. 43 as a function of F is for equilibrium melting experiments. This means that each melting experiment used in its construction is of constant composition and oxygen content, but variable temperature. As such, the experimental results are directly applicable for modelling equilibrium crystallisation, but not for fractional crystallisation, where the crystallised solid is removed from the system and thus the composition changes with progressive crystallisation and lower temperature. These instantaneous fractional crystallisation modes can be obtained as the derivatives to the equilibrium mode variations. Since these latter can be approximated by linear equations, fractional crystallisation can, because the slopes are constants, be modelled by constant modes.

Using this approach, Thy et al. (2006) constrained the plagioclase and olivine cotectic by a constant mode of 26 wt% olivine and 74 wt% plagioclase and the plagioclase, olivine and augite cotectic by 9 wt% olivine, 45 wt% plagioclase and 43 wt% augite. For conditions where pigeonite replaces olivine, the modes were calculated as 19 wt% pigeonite, 41 wt% plagioclase and 40 wt% augite. Estimates of the FeTi oxide modes are complicated by the restrictions in the low-temperature experimental data (Thy et al. 2009a). Two different hypothetical sets of modes were therefore used to approximate the addition of FeTi oxides to the fractionating assemblage. The first used the experimental results of Thy et al. (2006) and Toplis & Carroll (1995), suggesting constant FeTi oxide modes resulting in 8 wt% olivine, 37 wt% plagioclase, 36 wt% augite, 13 wt% ilmenite and 6 wt% magnetite or 34 wt% plagioclase, 33 wt% augite, 16 wt% pigeonite, 11 wt% ilmenite and 6 wt% magnetite, respectively, dependent on whether olivine or pigeonite is stable. This first set of FeTi oxide saturated modes produces a strong Si enrichment in the liquid lines of descent similar to that suggested by Hunter & Sparks (1987) and Toplis & Carroll (1996). The second set of modes is derived from the assumption that neither ilmenite nor magnetite modes are constant with progressive crystallisation, but rather decrease upward in the stratigraphy as TiO₂ and possibly Fe₂O₃ decreases. This was suggested by Thy et al. (2009a) by showing that both modal contents of ilmenite and magnetite decrease in the gabbros to about 5 wt% ilmenite and < 1 wt% magnetite in the UZc (Fig. 15). This latter set of FeTi oxide saturated modes produces a strong Fe enrichment in the liquid line of descent with similarities to those suggested by McBirney & Naslund (1990) and Tegner (1997).

Temperature is determined for olivine or pigeonite saturated melts by a linear correlation between the experimental temperatures and the melt content of MgO as:

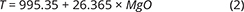
where T is temperature in °C, and MgO is the wt% content of MgO in the melt.

The compositions of the crystallising minerals are determined by either single or binary oxide-exchange coefficients either as functions of temperature or as constants. The Fe₂O₃ content of augite is calculated as a constant fraction of total iron (0.18) for the whole LS, while pigeonite Fe₂O₃ is assumed to be zero, and for ilmenite and magnetite the Fe₂O₃ contents are based on the results of Toplis & Carroll (1995) as functions of ΔFMQ. The fO₂ of the melt is calculated from the melt Fe₂O₃/FeO ratio and temperature is calculated using the formulation of Kilinc et al. (1983). The crystallisation order and zone and subzone divisions are modelled using iterative determinations of best fit to the observed An content of plagioclase and Fo content of olivine to constrain the appearances of augite, FeTi oxides and pigeonite. Apatite is not included in the calculations.

Based on the above assumptions and further details provided by Thy et al. (2006), the instantaneous composition of the solid fraction removed during fractional crystallisation can be calculated. The instantaneous melt compositions (or fractional crystallisation) can thus be modelled by solving sequentially the mass-balance equation:

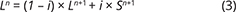
for the new melt Lⁿ⁺¹, knowing the previous melt Lⁿ and the new solid Sⁿ⁺¹ compositions, in steps from n = 1 to n = ∞ and a constant mass fraction of i for each step. The calculations will approximate perfect fractional crystallisation for i → 0 for which reason a practical value of 0.01 is used in the calculations (equivalent to steps of c. 1°C).

5.6.4 Results of forward modelling

Previous modelling has proposed two contrasting liquid lines of descents, both past FeTi oxide crystallisation, identified by either Si enrichment with restricted Fe enrichment (Hunter & Sparks 1987; Toplis & Carroll 1996) or by prolonged Fe enrichment with restricted Si enrichment (McBirney & Naslund 1990; Tegner 1997). Thy et al. (2006, 2009a) modelled these two contrasting liquid lines of descent using the same initial melt composition (Cm), oxygen fugacity at the initial FMQ, and silicate phase equilibria (Fig. 42C). The differences for the two liquid lines of descent were obtained by changing the modes of the FeTi oxides in the calculations. The Si-enrichment trend was modelled by using the experimental oxide modes, while the Fe-enrichment trend was obtained using oxide modes similar to those observed in the intrusion (Thy et al. 2006, 2009a). The resultant liquid lines of descent are summarised in Supplementary Tables S1 and S2 using total calculation steps of 180, solid fraction to 0.80–0.84 (F = 0.20–0.16) and T of 1162–1000°C.

The exposed stratigraphic column of the Skaergaard LS varies from F = 0.76 at the base of LZa to F → 0 at the top of the SH, using the volume interpretation of Nielsen (2004) and Eq. (1), relating F to stratigraphic height (m; Tegner et al. 2009). The stratigraphic height (or depth) for F = 1 is according to Eq. (1) at c. 365 m below the exposed base of the LS. To allow a direct comparison with observations, the forward modelling of the experimental melt compositions were broken into the same segments used throughout this study in the data tables. This is done by fitting polynomial curves to the forward modelling as functions of liquid fraction remaining and extrapolated to both F = 1 and F = 0. The results of this curve fitting are variably slightly negative for MgO, CaO and TiO₂ from upper UZa to UZb for which small positive values have been adopted for the calculations. The results of the curve fitting are summarised in Table 21 for the Si-enrichment models and in Table 22 for the Fe-enrichment models.

Table 22 Modelled iron enrichment melt compositions

Zone	Stratigraphic height (m)		F	T (°C)	LogfO2	SiO2	TiO2	Al2O3	Fe2O3	FeO	FeO*	MnO	MgO	CaO	Na2O	K2O	P2O5	Total	Pl	Ol	Pyroxene (Mg#)
	high	low				(wt%)	(wt%)	(wt%)	(wt%)	(wt%)	(wt%)	(wt%)	(wt%)	(wt%)	(wt%)	(wt%)	(wt%)	(wt%)	(An)	(Fo)
UBS	2169	2165	0.00	1012	–9.22	55.90	0.92	5.02	8.75	21.21	29.08	0.30	0.40	2.00	2.26	3.92	0.10	100.78	0.040	0.000	0.000
UZc	2165	2165	0.00	1020	–9.22	55.89	0.92	5.04	8.73	21.20	29.06	0.30	0.40	2.00	2.27	3.91	0.10	100.77	0.041	0.000	0.000
UZc	2165	2164	0.00	1025	–9.22	55.89	0.92	5.04	8.73	21.20	29.06	0.30	0.40	2.00	2.27	3.91	0.10	100.77	0.041	0.000	0.000
UZc	2163	2147	0.00	1021	–9.22	55.89	0.92	5.05	8.72	21.20	29.05	0.30	0.40	2.00	2.27	3.91	0.10	100.76	0.042	0.000	0.000
UZc	2144	2141	0.00	1027	–9.26	55.84	0.94	5.13	8.64	21.17	28.95	0.30	0.40	2.00	2.29	3.87	0.10	100.68	0.047	0.000	0.000
UZc	2091	2081	0.01	1037	–9.37	55.71	0.98	5.36	8.41	21.09	28.66	0.31	0.40	2.00	2.35	3.76	0.10	100.45	0.061	0.000	0.000
UZc	2075	2060	0.01	1036	–9.40	55.66	1.00	5.43	8.34	21.06	28.57	0.31	0.40	2.00	2.36	3.72	0.10	100.38	0.066	0.000	0.000
UZc	2060	2046	0.01	1042	–9.43	55.62	1.01	5.50	8.27	21.04	28.48	0.31	0.40	2.00	2.38	3.69	0.10	100.31	0.070	0.000	0.000
Uzb	2044	2030	0.02	1031	–9.47	55.57	1.03	5.57	8.20	21.01	28.38	0.31	0.40	2.00	2.40	3.65	0.10	100.24	0.075	0.000	0.000
UZb	2024	1984	0.02	1043	–9.51	55.52	1.05	5.66	8.11	20.97	28.27	0.31	0.40	2.00	2.42	3.61	0.10	100.14	0.081	0.000	0.000
UZb	1962	1921	0.03	1045	–9.64	55.32	1.12	5.96	7.81	20.86	27.89	0.31	0.40	2.00	2.49	3.46	0.10	99.83	0.100	0.000	0.000
UZb	1902	1862	0.04	1047	–9.77	55.12	1.19	6.26	7.51	20.75	27.50	0.31	0.40	2.00	2.56	3.31	0.10	99.50	0.120	0.000	0.000
UZb	1843	1801	0.05	1052	–9.90	54.90	1.27	6.56	7.20	20.64	27.12	0.31	0.40	2.00	2.63	3.15	0.10	99.16	0.140	0.000	0.000
UZb	1782	1748	0.06	1050	–10.03	54.66	1.35	6.88	6.89	20.52	26.72	0.31	0.40	2.00	2.70	2.99	0.10	98.80	0.161	0.000	0.000
UZb	1728	1691	0.07	1055	–10.14	54.43	1.43	7.15	6.61	20.41	26.36	0.31	0.40	2.00	2.76	2.85	0.10	98.46	0.180	0.000	0.000
UZb	1671	1630	0.09	1055	–10.25	54.17	1.52	7.45	6.32	20.29	25.98	0.31	0.40	2.00	2.82	2.70	0.10	98.09	0.201	0.000	0.000
UZb	1620	1600	0.10	1060	–10.34	53.94	1.60	7.70	6.07	20.19	25.65	0.31	0.40	2.00	2.87	2.57	0.10	97.74	0.219	0.000	0.000
UZa	1561	1527	0.11	1063	–10.44	53.65	1.70	7.99	5.78	20.06	25.26	0.31	0.40	2.57	2.93	2.41	0.10	97.91	0.240	0.000	0.000
UZa	1506	1431	0.13	1067	–10.52	53.36	1.79	8.25	5.52	19.95	24.91	0.32	0.40	3.19	2.98	2.27	1.89	99.93	0.260	0.000	0.000
UZa	1403	1343	0.15	1072	–10.65	52.81	1.99	8.71	5.06	19.73	24.29	0.32	0.40	4.29	3.05	2.02	1.65	100.03	0.297	0.014	0.064
UZa	1323	1282	0.18	1072	–10.72	52.35	2.14	9.04	4.74	19.56	23.83	0.32	0.42	5.07	3.09	1.83	1.47	100.05	0.324	0.058	0.143
UZa	1268	1237	0.19	1073	–10.75	52.03	2.26	9.24	4.54	19.45	23.53	0.32	0.57	5.57	3.11	1.71	1.36	100.16	0.343	0.089	0.196
UZa	1218	1188	0.21	1074	–10.76	51.74	2.36	9.42	4.37	19.34	23.27	0.32	0.72	5.98	3.13	1.61	1.26	100.25	0.359	0.117	0.241
UZa	1178	1131	0.22	1075	–10.76	51.50	2.44	9.55	4.24	19.26	23.07	0.32	0.86	6.30	3.13	1.53	1.19	100.31	0.372	0.140	0.277
MZ	1098	1055	0.25	1077	–10.75	51.02	2.61	9.77	4.02	19.09	22.70	0.32	1.13	6.85	3.13	1.38	1.05	100.40	0.396	0.186	0.343
MZ	1053	1032	0.27	1081	–10.73	50.75	2.71	9.89	3.91	18.99	22.50	0.32	1.30	7.13	3.13	1.31	0.98	100.43	0.410	0.211	0.377
MZ	1024	1009	0.28	1083	–10.71	50.58	2.77	9.96	3.84	18.92	22.38	0.32	1.42	7.30	3.12	1.26	0.94	100.45	0.418	0.228	0.399
MZ	1003	1002	0.29	1085	–10.70	50.46	2.82	10.00	3.80	18.88	22.29	0.32	1.50	7.41	3.12	1.23	0.91	100.45	0.424	0.240	0.414
MZ	988	961	0.29	1088	–10.68	50.37	2.85	10.03	3.77	18.84	22.23	0.32	1.56	7.49	3.11	1.21	0.89	100.46	0.428	0.249	0.424
MZ	953	930	0.30	1087	–10.65	50.16	2.93	10.10	3.70	18.76	22.09	0.32	1.71	7.66	3.10	1.16	0.85	100.46	0.438	0.269	0.448
MZ	921	900	0.32	1099	–10.62	49.98	3.00	10.16	3.65	18.69	21.97	0.32	1.85	7.80	3.09	1.12	0.81	100.47	0.447	0.287	0.468
MZ	890	875	0.33	1093	–10.58	49.80	3.06	10.21	3.60	18.62	21.85	0.32	1.98	7.93	3.07	1.08	0.78	100.46	0.455	0.304	0.487
LZc	847	816	0.35	1095	–10.52	49.56	3.16	10.27	3.54	18.51	21.70	0.32	2.18	8.09	3.05	1.03	0.74	100.45	0.467	0.328	0.511
LZc	808	798	0.36	1093	–10.47	49.35	3.24	10.32	3.49	18.41	21.56	0.32	2.36	8.23	3.03	0.99	0.70	100.44	0.477	0.350	0.532
LZc	784	742	0.37	1096	–10.43	49.23	3.29	10.35	3.47	18.35	21.47	0.32	2.47	8.30	3.01	0.96	0.68	100.43	0.483	0.363	0.544
LZc	723	703	0.40	1103	–10.33	48.92	3.41	10.42	3.41	18.19	21.26	0.32	2.77	8.46	2.97	0.91	0.63	100.41	0.498	0.395	0.573
LZb	703	681	0.41	1099	–10.29	48.82	3.45	10.44	3.40	18.13	21.19	0.32	2.86	8.51	2.95	0.89	0.62	100.40	0.503	0.405	0.581
LZb	634	580	0.44	1108	–10.16	48.51	3.58	10.49	3.35	17.93	20.95	0.32	3.21	8.66	2.90	0.84	0.58	100.37	0.519	0.440	0.608
LZb	558	488	0.47	1110	–10.01	48.20	3.72	10.55	3.31	17.69	20.67	0.32	3.59	8.81	2.83	0.79	0.54	100.34	0.537	0.476	0.634
LZb	447	367	0.53	1113	–9.79	47.83	3.88	10.64	3.26	17.30	20.23	0.32	4.15	9.00	2.74	0.73	0.50	100.34	0.562	0.525	0.664
LZb	346	221	0.58	1121	–9.60	47.59	3.99	10.75	3.20	16.90	19.78	0.31	4.65	9.18	2.66	0.68	0.46	100.38	0.585	0.564	0.686
LZb	177	173	0.67	1126	–9.32	47.41	4.06	11.05	3.06	16.12	18.87	0.30	5.44	9.58	2.54	0.61	0.41	100.58	0.623	0.617	0.717
LZa	161	137	0.68	1119	–9.30	47.41	4.06	11.09	3.04	16.04	18.77	0.30	5.51	9.63	2.53	0.60	0.40	100.60	0.627	0.622	0.719
LZa	125	107	0.70	1126	–9.25	47.41	4.05	11.18	2.99	15.85	18.54	0.30	5.67	9.73	2.52	0.58	0.39	100.67	0.635	0.631	0.725
LZa	96	27	0.71	1131	–9.21	47.41	4.03	11.26	2.95	15.70	18.35	0.30	5.79	9.82	2.50	0.57	0.38	100.72	0.641	0.638	0.730
LZa	7		0.76	1126	–9.13	47.47	3.93	11.57	2.81	15.21	17.74	0.29	6.14	10.12	2.48	0.53	0.34	100.89	0.660	0.658	0.743
F = 1	–365		1.00	1163	–8.90	47.67	2.53	13.70	2.22	13.22	15.22	0.25	6.36	10.53	2.42	0.44	0.28	99.62	0.696	0.739	0.787
Melt composition calculated from the silica-enrichment forward modelling by Thy et al. (2006) and reasonable values for P2O5 in UZc. FeO*: total iron as FeO. The modelled TiO2 and MgO becomes negative at F ~ 0.13 in the upper part of UZa and were fixed at small positive values for the rest of the stratigraphy. T is calculated from plagioclase An (mol%) content based on Thy et al. (2009b, 2013). F: fraction of melt remaining. Values in italic are assumed. See the Supplementary File S3 for complete modelling results. An and Fo as mole fractions.

Fig. 44A illustrates the two curve-fitted liquid lines of descent in terms of their FeO or FeO* contents, both as a function of SiO₂ (FeO* is the total iron calculated as FeO). As pointed out by Thy et al. (2006, 2009a) and discussed here, the difference in the enrichments for the two basic models are mainly due to differences in the amount of FeTi oxides removed from the magma, giving rise to the contrasting iron versus silica variations and contrasting evolutions of fO₂, as measured by the Fe₂O₃/FeO melt ratio (see Section 5.2). The forward modelling of perfect fractional crystallisation, using phase equilibria of evolved FeTi basaltic dykes associated with the intrusion, reproduces some aspects of the observed cryptic variation for plagioclase, olivine and clinopyroxene (Fig. 44B). The variations reproduced in the modelling is overall similar to the observed cryptic co-variation of the main silicate mineral phases – although some differences are apparent when considered in detail. Both the initial and the terminal co-variation of plagioclase and olivine and clinopyroxene fit the observed cryptic mineral compositions. The forward models reasonably reproduce variation in the LZ, while the MZ and UZ results deviate from the observed cryptic co-variation displaying more pronounced convex patterns (Fig. 44B). The reason for this can be attributed to the effects of Fe³⁺ that may not properly have been included in the Fe-Mg partitioning or due to the experimental conditions used in the experimental foundation for the forward modelling. What is perhaps more significant is that the observed coexisting mineral compositions (Fo_0.0 and An_~30) at the SH are reproduced already at F = 0.14, corresponding to somewhere in the upper part of the UZa (Fig. 44B). This can probably be attributed to the assumption of perfect fractional crystallisation and that a component of imperfect fractional crystallisation (equilibrium, in situ fractionation or liquid immiscibility) may be able to significantly delay fractionation to extreme values at F ≈ 0. A somewhat similar effect was seen in the cryptic variation (Fig. 30) that suggests fractionation ceases in the upper part of UZb.

Finally, there are few, if any, observable differences in the cryptic mineral variation of the two modelled liquid lines of decent, except at low values of F (Fig. 44B). This means that studies of the silicate cryptic mineral variation and the phase layering are unlikely to offer definitive conclusions as to the nature of the liquid lines of descent for the intrusion. The diverse proposed melt evolutions for the Skaergaard intrusion abundantly attest to this observation (Wager & Brown 1967; Hunter & Sparks 1987; McBirney & Naslund 1990; Toplis & Carroll 1996; Nielsen 2004; Andersen 2006; Thy et al. 2006; Tegner & Cawthorn 2010).

5.7 Additional phase-equilibria constraints

Basaltic melts, such as the parental melt to the Skaergaard intrusion, followed crystallisation and fractionation paths controlled by phase equilibria between melt and silicate and oxide minerals. However, the sampled gabbros represent the accumulated mixtures of variable proportions of solid minerals and a component representing the final trapped melts that only record the evolution of the parental melt and the phase equilibria indirectly. Early work used phase equilibria in simplified or haplobasaltic systems to understand the evolution of the Skaergaard and other layered intrusions (Osborn 1959, 1979; Presnall 1966; Biggar 1974; Maaløe 1976b). Later studies expanded the approach to multicomponent basalt systems (Irvine 1970a, 1979; Jackson 1970; Ford 1981). We here use the same approach by displaying the Skaergaard gabbro compositions graphically as projections of the pseudo-quaternary basalt system (Fig. 45) using the plagioclase, olivine, quartz and diopside (Di) components – the latter as a proxy for clinopyroxene (augite). This approach allows important principal observations to be made about crystallisation orders and the dominate mode of differentiation.

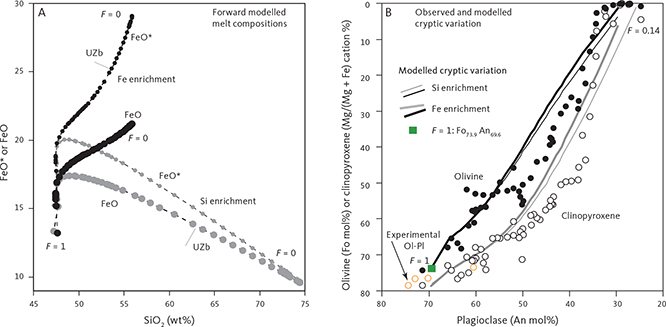
Fig. 44 Forward modelling of the liquid line of descent and the cryptic mineral variation for the preferred, initial Skaergaard magma based on Thy et al. (2006, 2009b). A: Melt composition of FeO or FeO* as a function of SiO₂ (wt%). The two end-member models (Fe or Si enrichment) are based of the solutions of Thy et al. (2006) and Toplis & Carroll (1996), respectively, extrapolated to F = 1 and F = 0 (F: melt fraction remaining). FeO* is total iron calculated as FeO. The difference between the curves for FeO and FeO* reflects the amount of Fe₂O₃. B: Olivine (Fo mol%) or clinopyroxene (Mg/(Mg + Fe) cation %) compositions as a function of plagioclase (An mol%). Data shown are from Tables 3–5 with additional primitive gabbro compositions from Thy et al. (2008, table 1). Iron in clinopyroxene is calculated as total iron. Solid curves: forward modelling, compared to the observed coexisting minerals in the LS. The experimental Ol-Pl is the coexisting olivine and plagioclase at the liquidus in the one-atmosphere melting experiment used to formulate the forward model (Thy et al. 2006). Green box: extrapolated coexisting plagioclase and olivine at F = 1. The forward modelling fails to reproduce the observations in UZc due to early modelled depletion of MgO to zero and is thus not shown past F = 0.16.

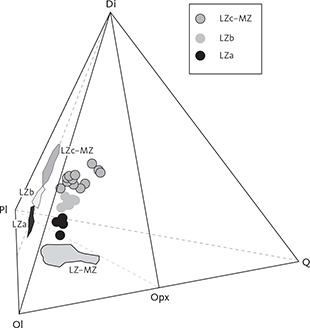
Fig. 45 Perspective view of the LZ–MZ gabbros in the quaternary olivine (Ol) – quartz (Q) – plagioclase (Pl) – diopside (Di) with projections onto the Di–Pl–Ol and Pl–Ol–Di triangles. A molecular equivalent norm, calculated based on the CIPW norm procedure, was used for the projection with ferric and ferrous iron as analysed. The gabbro compositions from Table 13 are grouped as LZa, LZb and LZc–MZ. For simplicity, the UZ is not shown.

5.7.1 Projection schemes

The analysed gabbros (Table 13) and silicate minerals (Tables 3–5, 8) are recast using a CIPW normative compositions (molecular norm) for plotting. The Fe₂O₃/FeO ratios for the bulk rocks were determined by wet chemistry, while all silicate minerals are assumed to be Fe₂O₃-free. The latter is a simplification for clinopyroxene, but we opted to do this given the difficulties of accurately constraining Fe⁺³ content from stoichiometry based on microprobe data (Fig. 22; see Section 4.3.3). Increasing the amount of ferric ion in clinopyroxene will shift these slightly towards higher normative quartz (Q), without changing the principal conclusions based on the Fe₂O₃-free assumption. Our projection scheme is similar to that used by Presnall et al. (1979) where forsterite + fayalite = olivine (Ol), anorthite + albite = plagioclase (Pl), and diopside (Di) + hedenbergite = Di. Enstatite and ferrosilite are combined as orthopyroxene (Opx) and plot midway between Ol and Q. The projections are from minor components like magnetite, ilmenite, and apatite. This means that to the extent these minor components conform to the simplified CIPW normative compositions, they will have no effect on the variability in the quaternary diagram. Three triangular projections of the quaternary are used to facilitate a three-dimensional understanding: the Di-Ol-Q (projected from Pl), the Pl-Ol-Q (projected from Di), and the Di-Pl-Ol (projected from Q). The compositions used in this discussion are, as shown in the tables, not individual analyses, but averages of three consecutive samples from the stratigraphy.

5.7.2 Crystallisation order and zone divisions

The normative compositions of the LZ gabbros plot in the quaternary close to the Di-Pl-Ol join, being olivine and hypersthene normative, without reaching into the quartz-normative volume (Fig. 45). The UZ gabbros (not shown) plot in the same general area as LZc–MZ, but with only UZc extending into the Q-normative volume. The Pl/Ol ratios (1.39 ± 0.28) are restricted compared to the more variable Di/Pl ratio that systematically increases upward from 0.32 ± 0.03 in LZa to 0.59 ± 0.12 in LZb and 0.93 ± 0.32 in LZc (Fig. 45).

In the ternary projections, LZc, MZ, and UZa gabbros cluster around the Ol-normative extension of the modelled liquid lines of descent (Fig. 46A) as would be expected for solid crystallisation products from a ferrobasaltic melts similar to those used for the present forward modelling (Thy et al. 2006, 2009a). They also cluster around the olivine and hypersthene normative segment of the experimental plagioclase, clinopyroxene and olivine multi-saturated cotectic (marked L_(pl,cpx,ol) in Fig. 46A) as expected for gabbros formed from crystallisation of these three silicate primocrysts from a large range of melt compositions (Thy et al. 2008).

The LZa gabbros with a low normative diopside content (Figs 46A, 47A) are consistent with early accumulation of primocrysts of plagioclase and olivine. This relationship is consistent with the zonal division based on petrography, where Wager & Brown (1967) and McBirney (1989a) defined the base of the LZb by a reduction in the amount of oikocrystic augite and appearance of granular augite (see Fig. 5). The transition occurs at a height of about 174 m (normalised to the stratigraphic scale adopted in this study, Fig. 1) and closely conforms to the marked increase in normative diopside. The LZb and LZc gabbros reflect an upward increasing accumulation of clinopyroxene with LZc eventually reaching a proportion of clinopyroxene predicted from experimentally-based modelling (Fig. 47A; Thy et al. 2006). This order of LZ crystallisation supports the observed zonal division, suggesting early concurrent crystallisation of plagioclase and olivine in LZa, followed by clinopyroxene in LZb, and finally adding FeTi oxide minerals (magnetite and ilmenite) in LZc, where the effects of the FeTi oxides are not, or only marginally, detected in the projection (Fig. 47A).

Fig. 46 Projections from quartz (Q) of the quaternary Ol–Q–Pl–Di on to the triangular Di–Pl–Ol diagram (see quaternary diagram, insert) in mol%. A: Projection for LZ–MZ. B: Projection for UZ. Projection scheme and abbreviations in Fig. 45. The gabbro compositions from Table 13 are grouped as LZa, LZb, LZc–MZ, UZa, UZb and UZc. Gabbro is calculated with ferric and ferrous iron as analysed, while all minerals (Aug: augite, Plag: plagioclase, Oliv: olivine, orthopyroxene/pigeonite and ferrobustamite) are calculated with all iron as ferrous iron. Average mineral compositions are from Tables 3–5, 8 for: Plagioclase and clinopyroxene (Aug; grouped as LZa–UZa and UZb–UZc), ferrobustamite, orthopyroxene, pigeonite and olivine. Approximate location of the join of Pl–Ol–Aug is marked by the grey shaded triangle. The black square labelled L_(Pl,Cpx,Ol) is the piercing, one-atmosphere, plagioclase-augite-olivine cotectic based on melting experiments of Thy & Lofgren (1992, 1994) and Thy et al. (1998, 1999).

Fig. 47 Projections from plagioclase (Pl) of the quaternary Ol–Q–Pl–Di on the triangular Di–Ol–Q diagram (see quaternary diagram, inset) in mol%. Data, projection methods and abbreviations in Fig. 45. The gabbro compositions are grouped as LZa, LZb, LZc–MZ, UZa, UZb and UZc. A: Projection for LZ–MZ. B: Projection for UZ. L_(Pl,Cpx,Ol) represents melt compositions coexisting with plagioclase, clinopyroxene, and olivine at variable temperatures (Thy & Lofgren 1992, 1994). +Pi indicates the appearance of pigeonite (Thy et al. 1998, 1999). The two curves marked ‘Fe enrichment’ and ‘Si enrichment’ are the Liquid Lines of Descent, which both terminate at the end of UZa (Thy et al. 2006, 2009a; Tables 21 and 22). Approx. location of the join Ol–Pi–Aug is marked by the grey shaded triangle. The general effect of non-quaternary normative components in magnetite (hercynite, Hr, and wüstite, Wü)is indicated by arrows directed away from Q.

Because the part of the LS sampled in this study does not reach into the lowermost HZ, the question of whether plagioclase or olivine were the initial crystallising silicate primocrysts cannot directly be resolved. Evidence from Cambridge Drill Core I suggests that the HZ gabbros, extending for at least 150 m and possibly more, below the exposed part of LZa, are similar to the upper part of the LZa (Maaløe 1976a; Holness et al. 2015). Holness et al. (2015) suggested that the Skaergaard magma was filled by several early pulses of plagioclase and olivine-bearing magma eventually leading to a ballooning of the chamber to its final size. This is consistent with the observation by Ariskin (2003) that the initial magma contained plagioclase and olivine phenocrysts.

The arrival of a new primocryst, like augite, is expected to result in a flattening of the liquidus and consequently in the increase in proportions of crystallisation (Wyllie 1963). An additional effect is an intermittent increase in latent heat release (Holness et al. 2007a, b, 2009) that is manifested in an increase in textural grain-boundary maturity effective until the excess heat dissipates. Holness et al. (2015) examined the lower part of the intrusion in detail, including the HZ, without being able to pinpoint equivocally the LZa–LZb boundary based on textural criteria like dihedral angles and maturity of the growth of augite in interstitial melt – although they did proposed a progressive transition between 100 and about 200 m depth in the Cambridge Drill Core.

Thus, it remains to be explained why the LZb gabbros occupy an intermediate position in the projections between LZa and LZc, when LZb and LZc could be expected to have similar olivine-plagioclase-clinopyroxene proportions (Figs 46A, 47A). There are several explanations although none of these are conclusive. The first explanation is that the LZb parental melts were not saturated in augite, despite the petrographic indications, but, like LZa, were only saturated in olivine and plagioclase. The augite component in this case may have originated from a crystallised component of trapped melt estimated from 40 to 10% upward (Tegner et al. 2009) in an olivine and plagioclase mush and not in a mush of augite, olivine and plagioclase. Modelling the solidification of such a mush for the high melt content, assuming a fractionation path similar to that for the entire LS and near augite saturation in the trapped melt (Thy et al. 2006), results in a felsic gabbro at the base of LZb composed of 20 wt% olivine, 65 wt% plagioclase and 15 wt% augite (on a weight basis) plus lesser amounts of orthopyroxene and FeTi oxides. A calculation assuming closed equilibrium crystallisation (Thy et al. 2006) predicts rather similar modes of 15% olivine, 68% plagioclase and 12% augite. Thus, despite demonstrating that substantial augite can be formed from the trapped melt, both models fall well short of predicting the 28% augite found in the LZb (Table 1). Furthermore, the amount of trapped melt decreases substantially upward to a quarter of that from the base of LZb (Tegner et al. 2009) and consequently, the modelled modal augite reduces proportionately, assuming cotectic plagioclase and olivine saturation in the main magma. A second, or alternative, explanation is that the trapped-melt content in the LZ may be underestimated, thus allowing for a higher effect of interstitial crystallisation of clinopyroxene. However, required amounts by far exceed possible estimates in this study (see Section 5.12.6).

The texture of the LZb suggests co-crystallisation of plagioclase, olivine, and augite and that the gabbros were controlled by liquids, in turn controlled by these three silicate phases. This implies a cotectic shift towards lower augite modes, relative to the univariant cotectic shift determined for low-pressure North Atlantic lavas – including East Greenland lavas and Skaergaard-related dykes (Fig. 47A; Thy & Lofgren 1992, 1994; Thy et al. 1998, 1999, 2006, 2008). Such a shift was not detected for Skaergaard-related dykes and therefore not included in the experimental data used to forward model the Skaergaard magma. Cotectic shifts for low-pressure conditions have been suggested for olivine-normative compositions. In particular, works by Walker et al. (1979) and Presnall et al. (1979) have suggested a marked increase in normative plagioclase in olivine-hypersthene normative melts approaching the Ol-Pl-Di join. Later experimental work covering the full melt range of nepheline to hypersthene normative compositions has, however, been unable to support significant cotectic deviations from linearity like that shown in Fig. 47 (Sack et al. 1987).

We suggest that neither differences in the trapped-melt content nor shifts in the olivine-plagioclase-augite cotectic offer plausible explanations for the low modal pyroxene-content in the LZb, and so other explanations must be sought. There is a systematic difference in the texture of LZb, compared to the subzones below and above, namely a general increase in average grain size concurrently with a change in the pyroxene fabric from an oikoclastic fabric in LZb to a dominating granular fabric in LZc (cf. Fig. 5). It is possible that this textural variation can be related to variation in crystallisation conditions across the LZ and that this could be seen as a suppression of augite crystallisation concurrently with an increase in grain size in the LZb. The variation in crystallisation conditions such as pressure and water activity are expected to affect the relative saturation of augite and other silicate phases. Increasing dry pressure is expected to raise augite saturation at the expense of olivine and plagioclase (Stolper 1980; Grove & Kinzler 1992; Berndt et al. 2005; Whitaker et al. 2007) but this is not a realistic explanation (see Section 5.3). The effects of increasing water activity in the melt are known to depress the appearance of augite at the expense of olivine and plagioclase in basaltic melts (Almeev et al. 2007, 2012; Botcharnikov et al. 2008) and probably also to increase the grain size. However, the Skaergaard gabbros lack any compositional and mineralogical evidence to suggest that they originated from anything other than nominally dry melts (see Section 5.9).

Finally, the low augite proportions in LZb could be attributed to a biased sampling procedure, resulting in gabbros that do not represent the original mush composition, perhaps due to the relatively coarser grain size compared to the zones above. However, in view of the sampling results for both LZa and LZc and the systematic sampling of the felsic LZb gabbros, such a sampling bias is not considered plausible.

5.7.3 Clinopyroxene crystallisation

Clinopyroxene occupies an elongated volume close to the Di-Ol join (Fig. 46). When projected from Pl onto the triangle Di-Ol-Q, as shown in Fig. 47 and in more detail in Fig. 48, a systematic variation with decreasing diopside content in the LZ and MZ can be seen as a function of stratigraphy in the LS (Fig. 48A). This decrease is followed by an increase upward in the UZ (Fig. 48B). This variation mirrors that seen in the diopside content of the pyroxenes forming a keel at the boundary between the MZ and UZa (Figs 19, 21). The result is that clinopyroxene plots with decreasing normative diopside up through the stratigraphy until the MZ. Thereafter the trend reverses to increasing diopside forming a narrow v-shaped pattern (Fig. 48B). As pointed out by Coombs (1963), this pattern is also reflected in the original Skaergaard pyroxene analyses on separated minerals by Brown et al. (1957) and Brown & Vincent (1963; Fig. 48C). Incorporating Fe³⁺ in the calculations will have an insignificant effect.

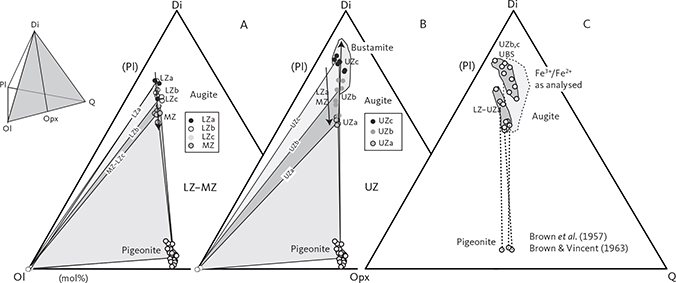
Fig. 48 Pyroxene variation as a function of LS zones and subzones in the plagioclase (Pl) projection on the Ol–Di–Q triangle of the quaternary Ol–Q–Pl–Di (see quaternary diagram, inset) in mol%. Abbreviations in Fig. 45. The average pyroxene compositions from Tables 5, 7 and 8 are shown for each zone and subzone of the LS. A: Projection for LZ–MZ. B: Projection for UZ. C: Projection for Skaergaard pyroxene analyses on separated minerals by Brown et al. (1957) and Brown & Vincent (1963), assuming either all iron as ferrous iron (dark grey) or as originally analysed (light grey). Approximate variation in the locations of the join of Olivine–Pigeonite–Augite is marked for the LS subzones by grey shaded triangles. UBS: Upper Border Series.

Fig. 49 Normative fraction of diopside (Di) of the modelled liquid line of descent (Normative Di/(Di + Ol + Q) melt model); Si-enrichment trend; Table 21) vs. the same fraction for observed clinopyroxenes (normative Di/(Di + Ol + Q) pyroxene). Average values for the individual zones and subzones of the LS are shown. Abbreviations in Figs 2, 45.

Variation in the normative pyroxene composition leads to an overall increase in modal clinopyroxene content upward in the stratigraphy throughout the LZ to MZ, followed by a corresponding drop in the UZ. The result is a dramatic change in the slope of the fractionation path at the MZ–UZa boundary, accelerating fractionation towards increasing normative Q (Fig. 49). This is seen on many binary and ternary variation diagrams illustrating the mineral compositions and the melt evolution throughout this study. It is an interesting consequence that while the melt composition is dominantly quartz-normative, the resulting gabbros are consistently olivine and hypersthene-normative.

5.7.4 FeTi oxide crystallisation

The minor normative components apatite, ilmenite, hematite and magnetite were excluded from the projection scheme on the assumption that their compositions are nearly identical to the normative components. This is true for natural apatite and for ilmenite for which hematite is calculated as a separate normative component. However, the norm calculation for natural magnetite assumes ideal magnetite (FeO^.Fe₂O₃) and in effect calculates ulvöspinel (2FeO^.TiO₂) as ilmenite (FeO^.TiO₂) and hematite (Fe₂O₃). An occasional small amount of normative rutile (TiO₂) is ignored. While ilmenite is close to the ideal composition (with hematite being part of the ilmenite solid solution), the magnetite of the Skaergaard intrusion (Table 9) has an average normative composition of 84 wt% magnetite, ilmenite and hematite with the remaining made up of 16 wt% excess wüstite (FeO) and corundum (Al₂O₃). The latter two components can be recast as 1 wt% hercynite (Hr, FeO^.Al₂O₃) and 15 wt% wüstite (Wü, FeO). The effect of these non-quaternary components will be to shift the position of the FeTi oxide-bearing cumulates away from Q in the triangular diagram projected from Pl (Thy 1995; Fig. 47A). This non-quaternary shift may affect LZc, the MZ and UZa, in decreasing magnitude determined by their amounts of magnetite, relative to LZa and UZb. This effect must be considered when interpretating the details of the normative projections, but is not large enough to significantly affect the principal interpretation of the present phase equilibria, except for a minor shift of the LZc–MZ gabbros away from Q compared to the UZa gabbros (Fig. 47A).

5.7.5 Orthopyroxene crystallisation

The status of orthopyroxene in the lower parts of the LS has been viewed as either a primocryst (Wager & Deer 1939; Wager & Brown 1967; Irvine et al. 1998) or a late phase-replacing olivine and clinopyroxene (McBirney 1989a; McBirney & Naslund 1990; Tegner et al. 2009). The latter would include crystallisation of orthopyroxene replacing olivine from the trapped melt (McBirney 1989a), subsolidus lamellae exsolution and coarsening from high-Ca clinopyroxene (Lindsley & Andersen 1983) or both. The projections from plagioclase onto the triangle Ol-Di-Q (which includes Opx) have some bearing on this discussion (Fig. 50).

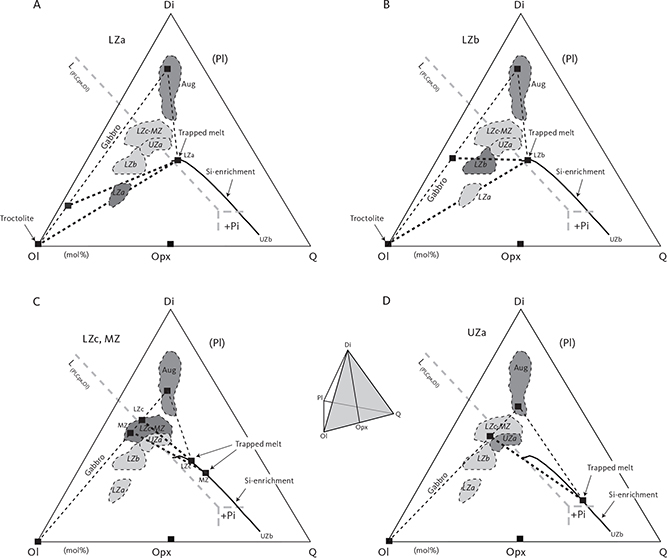
Fig. 50 Summary interpretations of projections from plagioclase (Pl) of the quaternary Ol–Q–Pl–Di on the triangular Di–Ol–Q diagram (see quaternary diagram, inset) in mol%. A: Projection for LZa. B: Projection for LZa. C: Projection for LZc and MZ. D: Projection for UZa. Data, projection methods and abbreviations in Fig. 45. Outlines of the zone and subzones of the LS are shown and interpreted in terms of modal gabbro compositions on the join of Ol–Aug and trapped melt composition on the Si enrichment liquid line of descent. L_(Pl,Cpx,Ol) represents melt compositions coexisting with plagioclase, clinopyroxene, and olivine at variable temperatures (Thy & Lofgren 1992, 1994). +Pi indicates the appearance of pigeonite (Thy et al. 1998, 1999).

The existence of a reaction relationship between olivine primocrysts and melt to form pigeonite has been demonstrated experimentally for relevant Skaergaard parental melts (Hoover 1989a; Snyder et al. 1993; Thy et al. 1998, 1999, 2006) to occur at c. F = 0.3, approximately coinciding with the LZc–MZ boundary. Based on these experiments, the reaction relationships are approximated by 0.9 liquid + 0.1 olivine = 0.2 pigeonite + 0.4 plagioclase + 0.4 clinopyroxene (see Thy et al. 2006). Thus, at the level of the LZa, closed crystallisation of the trapped melt estimated by Tegner et al. (2009) could result in c. 5–6% pigeonite. This would necessarily have decreased markedly upward as a function of the decrease in the total amount of trapped liquid. The saturation of pigeonite in equilibrium melting experiments occurs at an invariant reacting point in quartz-normative melts (marked ‘+pig’ in Fig. 50) after the saturation of FeTi oxides. However, the corresponding pigeonite saturation point during fractional crystallisation is uncertain, and judging from the present forward modelling, it may occur in less quartz-normative melts in the MZ.

These considerations point to the importance of pigeonite crystallisation (later inverted to orthopyroxene) during solidification from the interstitial melt of the mush. Orthopyroxene exsolution and coarsening of lamellae are also evident in the pyroxenes formed during cooling at near solidus to subsolidus conditions and may have affected the orthopyroxene content. The similarity between the bulk clinopyroxenes analysed by Brown et al. (1957) and Brown & Vincent (1963) and those obtained using the broad-beam technique with an electron microprobe (Fig. 19) suggests that exsolution may have had some, but limited effect, on the pyroxene proportions. It thus appears reasonable to reduce the gabbro compositions to the ratio between olivine and clinopyroxene after adding orthopyroxene to olivine as in Fig. 50. Using this procedure, the average MZ–UZc gabbro is calculated as containing 78 mol% clinopyroxene on the Ol-Aug join (Fig. 50C). This compares well to the intersection with the known three-silicate phase co-saturate in basaltic melt (76% clinopyroxene) but is very different if orthopyroxene is not added (85% clinopyroxene).

The composition of the LZa gabbros can thus be explained by a mixture of olivine (and plagioclase) and trapped melt and does not require primocryst orthopyroxene (Fig. 50A). This is consistent with the observation that primocrysts in the LZa were olivine and plagioclase. The modal orthopyroxene content of the gabbros (Tables 1 and 2) is thus mostly due to interstitial melt crystallisation. The LZb gabbros can likewise be interpreted as a mixture of olivine, plagioclase, augite and interstitial melt (Fig. 50B) and does not require orthopyroxene in excess of that crystallised from the interstitial melt – although the low augite content is still unresolved. For the remaining stratigraphic sequence, including the MZ, there is likewise no evidence that orthopyroxene exceeds the amount that could have crystallised from the interstitial melt.

The mode of orthopyroxene in the MZ can be estimated from this study as an average of 6% pigeonite, varying between 3% and 8% (Table 2). The modal content of orthopyroxene increases at the expense of olivine upward from the central part of the MZ (Figs 9, 15). Such amounts are similar to the bulk-gabbro content of the LZ, but far from the expectations for pigeonite (c. 15%) being a liquidus phase in the MZ based on the existing experimental information on Skaergaard-like basalt compositions (Hoover 1989a; Snyder et al. 1993; Thy et al. 1999, 2006). The available experimental evidence points to a hypersthene-normative parental melt where olivine is replaced by orthopyroxene during crystal fractionation (Grove & Bryan 1983; Grove & Baker 1984; Longhi & Pan 1988; Grove & Juster 1989; Veksler 2009). This suggests that the parental Skaergaard melt was hypersthene (and olivine) normative and fractionated towards an increasing quartz-normative composition (Toplis & Carroll 1995, 1996; Thy et al. 2006). What is less clear from the petrological evidence is, however, whether pigeonite was on the liquidus in the MZ. The alternative view, consistent with observations, is that pigeonite was a near-liquidus phase, crystallising from an interstitial melt throughout most of the lower part of the intrusion and never reached the liquidus prior to the interruption of fractional crystallisation by liquid immiscibility in the UZb.

5.7.6 Constraints on trapped-melt compositions

The gabbros analysed here can be evaluated in the normative projections as mixtures of primocrysts (olivine, plagioclase and pyroxenes) and trapped melt, now represented by a mixture of the same three minerals. A simplified interpretation is shown in Fig. 50 as projections from plagioclase onto the triangular Ol-Pl-Q diagram. The evaluations are based on the modelled liquid lines of descent showing Si enrichment (Table 21). However, using the Fe-enrichment trend (Table 22) will not significantly change the interpretation (compare with Fig. 47A). Average gabbro compositions in the subzones are projected to the Ol-Aug join using the modal compositions of Table 2 with orthopyroxene added to olivine and thus assuming that all orthopyroxene is a reaction product. To do this, we treat gabbro compositions as a mixture of olivine, augite and trapped-melt composition obtained from our forward modelling. The three-component system is then finally reduced to a binary system along the Ol-Aug join and the proportions of primocrysts and trapped melt are calculated using the lever rule (Fig. 50). This exercise shows that the composition of LZa can be accounted for as a mixture c. 40% olivine gabbro and c. 60% trapped melt (Fig. 50A). The general LZa field, nevertheless, transgresses towards the equilibrium cotectic proportions and the overlying gabbro zones. However, these do not reach the cotectic proportions predicted for basaltic systems on the Ol-Di join (L_(Pl,Cpx,Ol)) of Fig. 47). The LZb can be interpreted as a mixture of c. 60% olivine gabbro and c. 40% trapped melt (Fig. 50B). The LZc and MZ are made up of gabbros with relatively similar clinopyroxene content and trapped melt of 15–20% (Fig. 50C). For UZa, we estimated c. 10% trapped melt (Fig. 50D). These values of trapped melt, although also displaying an upward decrease, are significantly higher than those estimated by Tegner et al. (2009) and in this study (see Sections 5.11.4 and 5.12).

5.7.7 Field of liquid immiscibility

The modal variation in the UZ displays a marked increase in olivine near the base of UZb, followed by decreasing olivine and a concurrent increase in augite upward in UZb (Fig. 51). We consider the possibility that this marked increase in olivine near the base of UZb is a consequence of liquid immiscibility by comparing our observations to the experimental immiscibility results of Charlier & Grove (2012). Fig. 52A (projection from Pl) and Fig. 52B (projection from Di) compare the experimental melt just prior to immiscibility (Bc, binodal cusp) and the two conjugate immiscible melt compositions (“Fe” and “Si” in Fig. 52; compare to Fig. 47A). The modelled liquid compositions at the base of UZb correspond to the cusp-melt compositions of Charlier & Grove (2012) at the unset of immiscibility. There is also as a good correspondence between the Si-rich conjugate melt (“Si” in Fig. 52) and the various granophyre compositions observed in the Skaergaard intrusion (“Bt”, “T” and “G” in Fig. 52).

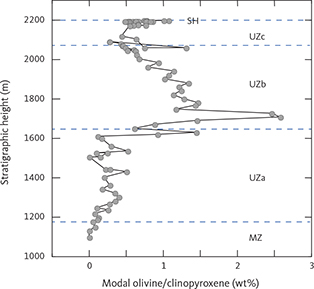
Fig. 51 Variation in the ratio between modal olivine and clinopyroxene (molar weight fractions) as a function of stratigraphic height (m) in the UZ. Subzone divisions for MZ, UZa, UZb and UZc and SH are shown (abbreviations in Fig. 2).

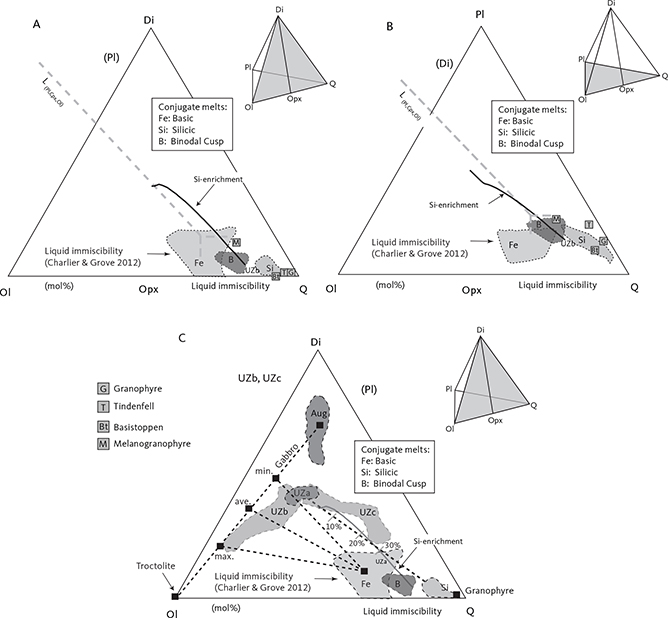
Fig. 52 Interpretation of liquid immiscibility. Projections from plagioclase (Pl) and diopside (Di) of the quaternary Ol–Q–Pl–Di on the triangular Di–Ol–Q and Pl–Ol–Q diagrams (see quaternary perspective diagrams, inset) in mol%. Projection method in Fig. 45. A: Experimental result of Charlier & Grove (2012) projected from Pl. B: Experimental result of Charlier & Grove (2012) projected from Di. C: Interpretation of UZ gabbros based on the results of Charlier & Grove (2012). The binodal cusp melt is denoted by ‘B’, which resolved to the Fe-rich and Si-rich conjugate melts with cooling. The granophyre melts of Table 18 are given by square symbols marked by ‘G’ (granophyre), ‘M’ (melanogranophyre), ‘T’ (Tindenfell) and ‘Bt’ (Basistoppen) in panels A, B. The additions of granophyre are marked on the UZa-granophyre join (10%, 20%, 30% in panel C). Solid curves: liquid lines of descent. max.: maximum. ave.: average. min.: minimum.

Figure 52C compares the UZ gabbros to the experimental immiscibility results. The first order observation is that the UZb and UZc fields intersect at the location of UZa and branch out from here towards either normative Q (or granophyre) for UZc or towards Ol (or troctolite) for UZb. This suggests that UZa is made up of gabbros formed prior to the onset of immiscibility. After immiscibility reaches the liquidus at the base of UZb, partial separation of the two conjugate melts results in UZb gabbros affected by enrichment in the basic-melt component and the UZc gabbros affected by enrichment in the silicic melt. Using the experimental determination of the two conjugate-melt compositions (Charlier & Grove 2012), UZc is made of a mixture of gabbro and up to 30% granophyre – not so different from the maximum UZc content of 20% granophyre detected in this study (see Section 5.4). The silicic conjugate melt and the granophyre are probably located near pseudo-invariant crystallisation (Grove et al. 1982) and are saturated in pyroxene, albite (An_~0 and not An₃₀ as in the host gabbros), quartz and probably orthoclase consistent with the UZc near the SH (Figs 13–15).

The UZb gabbros can be interpreted as mixtures of gabbros and basic conjugate melt (Fig. 52C) in relatively constant proportions of normative Di/Q (or clinopyroxene/granophyre) and highly variable olivine (Fig. 51). The content of the conjugate basic melt varies from 6% to 20% and is positively correlated with diopside (or clinopyroxene) content. The strong enrichment in normative olivine is consistent with the observed modal content (Fig. 15). In effect, this ultimately results in a magma chamber originating from enrichment in the basic conjugate melt at the base of UZb and enrichment in the silicic conjugate melt at the top of the chamber and in the UBS. With further cooling, the remaining magma will eventually exit the immiscibility field and proceed to solidify upward from the base of the UZb and downward from the UBS, terminating at the SH.

The basic conjugate melt resulting from liquid immiscibility falls within the olivine field and can be predicted after termination of immiscibility to crystallise this phase, initially without large amounts of plagioclase and augite (Fig. 52C) and thus resulting in an enrichment of olivine at the base of the UZb (Fig. 51). With increasing crystallisation, the modal content of olivine decreases, and augite and plagioclase increases, and eventually augite is restored on the liquidus. The silicic conjugate plots near quartz saturation or would eventually end in a crystallising quartz together with albitic plagioclase. However, in the projections both conjugate melts fall close to a pigeonite field and could eventually be expected to become saturated in pigeonite (e.g. Grove et al. 1982). Despite this, orthopyroxene crystallisation appears to have been terminated in upper UZa and does not appear in UZb or UZc. The reason for this is not clear but could be related to a thermal divide on the reaction curve between pigeonite and orthopyroxene as suggested by Grove et al. (1983). It could also be an artifact of not incorporating ferric iron in the immiscibility melt compositions, or a limitation in our understanding of the low-temperature phase equilibria of silicic melts.

An interpretation of the temperature of onset of liquid immiscibility on the Skaergaard liquid lines of descent is shown in Fig. 53 as a function of the melt structure measured by non-bridging oxygens per tetrahedral-coordinated cations (NBO/T). The modelled Skaergaard liquids (Tables 21, 22) reach into the two-liquid domain, although without any experimentally-derived sign of immiscibility (Thy et al. 2006). This penetration occurs at a higher temperature (c. 1060°C) than expected from the delineation of the two-liquid field of Charlier & Grove (2012; c. 1000–1020°C), as well as for other experimental studies of immiscibility in natural basalts (Dixon & Rutherford 1979; Philpotts & Doyle 1983). Veksler et al. (2007, 2008) have, nevertheless, proposed liquid unmixing at temperatures of 1110–1120°C based on centrifugation experiments on a composition believed to be representative for the MZ of the Skaergaard, although such high temperatures have been widely challenged (Philpotts 2008; Morse 2008b; Charlier & Grove 2012) and are not supported in this study. Nevertheless, intermediate temperatures in the range of 1050–1060°C may be possible, although not yet demonstrated experimentally (Charlier & Grove 2012; Honour et al. 2019a). Honour et al. (2019b) examined immiscibility in tholeiitic glasses and found an apex temperature for initiation of immiscibility at about 1125–1115°C (Kilauea Iki and Laki lavas), based on the MgO content of the glass. Such various estimates of the onset of immiscibility are thought to be controlled by compositional and melt structure in the bulk melts with compositions ranging from alkalic, to transitional or olivine tholeiitic and quartz tholeiitic.

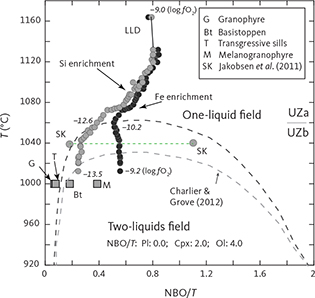
Fig. 53 Interpretation of the temperature (T; °C) of onset of liquid immiscibility as a function of the degree of polymerisation measured by non-bridging oxygens divided by temperature (NBO/T). The evolution paths for the two liquid line of descent calculations are from Tables 21 and 22. Italic numbers are modelled log fO₂ (Thy et al. 2006). Granophyre compositions are based on those in Table 18. The two analyses marked ‘SK’ and connected by a horizontal green dashed line are the conjugate melt estimated for the Skaergaard intrusion by Jakobsen et al. (2011, arbitrarily plotted at 1040°C). The lower boundary (grey dashed curve) between the ‘one liquid’ and ‘two-liquids’ fields are from Charlier & Grove (2012). The upper boundary (black dashed curve) is predicted from the Skaergaard intrusion raised to the location of the UZa–UZb boundary. Pl: plagioclase. Cpx: clinopyroxene. Ol: olivine.

The onset of immiscibility in the Skaergaard intrusion is interpreted to have occurred at the UZa–UZb boundary at c. 1060°C and to have been saturated in plagioclase (An₄₀), olivine (Fo₃₉), clinopyroxene (Mg# 50), FeTi oxides and possibly apatite at that point. The two modelling options suggest a 65% SiO₂ content in melt and 14% FeO* (for Si enrichment) or 54% SiO₂ and 26% FeO* (for Fe enrichment). The former shows some similarities with the results of Charlier & Grove (2012) for their starting composition for the Sept Iles sill, suggesting 60% SiO₂ and 10% FeO*. Their corresponding minerals are plagioclase (An₃₇), olivine (Fo₄₃), clinopyroxene (Mg# 54), FeTi oxides, apatite and pigeonite. Although there are some common mineralogical and compositional characteristics, the Skaergaard immiscibility appears to have occurred for melt compositions significantly less evolved and at a higher temperature than those for the Sept Iles sill. These differences are not explained but may be related to the relatively alkalic nature of the Sept Iles sill as revealed by its augite compositions. Philpotts (1979) found that the temperature of onset of immiscibility would rise from 1020°C to 1050°C as a result of increasing the log fO₂ from –13 to –9. Or in other words: with increasing fugacity, liquid immiscibility will occur at earlier stages of crystallisation. The present modelling of the liquid lines of descent suggests an log fO₂ at the onset of immiscibility of between –10.2 and –12.6, respectively for Fe enrichment and Si enrichment (Fig. 53). Thus, a lower fO₂ cannot have contributed to the unusual high temperature at immiscibility in the Skaergaard intrusion compared to the experiment at –9.0 FMQ of Charlier & Grove (2012).

It is also plausible that the difference in melt compositions between the Skaergaard liquids and those included in the experiments of Charlier & Grove (2012) may contribute to some of the anomalies encountered for the olivine-hypersthene normative-parental Skaergaard melt. Charlier & Grove (2012) demonstrated that immiscibility is possible for large SiO₂ and FeO* melt variations, including in effect both liquid lines of melt model considered here. They also demonstrated that Na₂O and non-quaternary oxides (K₂O, P₂O₅ and TiO₂) would promote immiscibility at a lower FeO* enrichment. Fractional crystallisation of parental Skaergaard melts, following augite and subsequently FeTi oxides crystallisation, would result in systematic increases in SiO₂ accompanied by Na₂O, K₂O and P₂O₅ enrichments (with variable FeO*). It is possible that such variations in fractional crystallisation may promote immiscibility at higher temperatures than implied by the equilibrium experimental determination of Charlier & Grove (2012), even though bulk-melt compositions may have been similar.

The melt structure described by the NBO/T ratio suggests that the Skaergaard intrusion reached the field of liquid immiscibility in polymerised melts with NBO/T values of 0.32 and 0.55, respectively, for the Si-enriched and Fe-enriched liquid lines of descent (Fig. 53). This is significantly higher levels of polymerisation than for the initial Skaergaard melt at 0.80 and is the result of substantial augite and FeTi oxide crystallisation. Using the lever rule, the relative proportions of the two conjugate immiscible melts can be estimated at 84–72% silicic and 16–28% basic melts, with the range given for the two liquid decent models, respectively. If the NBO/T ratios were extrapolated to the bimodal surface, without considering the effects of fractional crystallisation, we would obtain ratios of about 1:1 – more akin to equilibrium crystallisation than fractional crystallisation as assumed in the calculations of the UZ liquid lines of descent (see Sections 5.11.9 and 5.13). The liquid lines can be predicted to have penetrated from the immiscibility field into either a low-temperature single silicic melt field, by reaching a low-temperature subliquidus surface (Charlier & Grove 2012), or from a breakdown of immiscibility due to removal of silicic melt from the system. However, the relevant phase relations that would allow firm predictions are not known (Fig. 53).

For an immiscibility field nested on a cotectic (as in the case of the Skaergaard magma) to leave a detectable imprint on the liquid descent and solid fractionation products, disturbances of the immiscible melts are required such as gravitative separation or coalescence of one or both of the cognate melts. Without disturbances and with cooling and crystallisation, the immiscible field will disappear and leave no imprint on magmatic evolution (Roedder 1978, 1979), except perhaps the droplets trapped in zoned primocrysts and interstitial crystallisation products (Jakobsen et al. 2005, 2011). The olivine-rich base of the UZb is such a disturbance in the immiscibility processes.

5.7.8 Apatite crystallisation

Primocrystic apatite appears suddenly and at relatively high abundance reaching 8% at the boundary between UZa and UZb. The apatite abundance positively correlates with olivine (Fig. 54) and suggests that apatite, like the concurrent olivine base, may also be an effect of a liquid immiscibility event.

Fig. 54 Modal content of apatite (wt%) as a function of modal olivine (wt%). Curve is visual estimate and excludes outliers.

Watson (1979) showed apatite saturation to be a function of temperature and melt composition (particularly SiO₂ and P₂O₅) in basaltic to andesitic melts. Tollari et al. (2006) further showed that CaO had a large effect on apatite saturation, while varying iron and oxygen fugacities had little effect. Thus, the P₂O₅ content for apatite saturation decreases with increasing SiO₂ and CaO (Watson 1979; Green & Watson 1982; Tollari et al. 2006). Consequently, apatite may be stable in very felsic melts like granophyres (Watson & Capobianco 1981). Our forward modelling (Table 21) suggests crystallisation along the Si-enriched liquid line of descent using the saturation model of Tollari et al. (2006) when the melt reaches c. 2.0 wt% P₂O₅, similar to the prediction of Tegner et al. (2009, c. 1.7% P₂O₅), when the UZa–UZb boundary is taken to be 1060°C (Fig. 55). In contrast, apatite saturation is never reached along the Fe-enriched liquid line of descent using the same saturation model as Tollari et al. (2006). This means that apatite would reach stability at the UZa–UZb boundary for a Si-enrichment trend only and would remain stable at low temperatures in silicic-derived melt.

Fig. 55 The P₂O₅ concentrations (wt%) of melt saturated in apatite as a function of temperature (T; °C), calculated using the equation of Tollari et al. (2006) and the forward modelled liquid line of descent (LLD Si-enrichment; Table 21). The two curves only intersect at the UZb–UZa boundary (indicated by grey arrow), and thus apatite may thus first have become a liquidus phase at the onset of liquid immiscibility in the Skaergaard intrusion.

Using the partitioning of P₂O₅ between the two conjugate melts determined by Watson (1976; D^B/S = 10), the P₂O₅ content of the basic conjugate melt would, because of the high D value, have had nearly the same P₂O₅ content (c. 1.8 wt%). This means that most of P₂O₅ would go into the basic conjugate melt and that the presence of apatite in the Skaergaard intrusion could be controlled by liquid immiscibility and not crystal fractionation.

It is thus not possible to determine conclusively whether apatite appearance at the UZa–UZb boundary is a result of protracted fractionation or the result of immiscibility and the accumulation of basic conjugate melt at the boundary. Both scenarios would be able to explain the upward decreasing modal content of apatite. This would be for fractional crystallisation due to decreasing P₂O₅ and for liquid immiscibility due to upward increasing granophyre The positive correlation between modal apatite and the ‘excess’ olivine at the base of UZb is nevertheless seen as a strong indication that the appearance of apatite, like olivine, is related to the onset of liquid immiscibility.

5.7.9 Bulk-rock compositions and cotectic relations

It is conspicuous that the majority (LZc–UZa) of the Skaergaard gabbros (Figs 46, 47) cluster around the experimental determination of the cotectic for basaltic melts saturated in plagioclase, olivine and clinopyroxene (Thy & Lofgren 1992, 1994). This would imply that the gabbros formed from the accumulation of three primocryst silicate phases (plus FeTi oxides and apatite) and trapped melt, without recording excessive phase separation either from crystallisation or gravitative sorting. This is clearly not the case since there is abundant evidence that extreme primocryst sorting or separation is related to extensive layering in the outcrops of the Skaergaard intrusion (e.g. Wager & Deer 1939; Irvine 1987; Maaløe 1987; Naslund et al. 1987; Conrad & Naslund 1989). The good correspondence with expected phase boundaries can be explained simply by the field-work approach of targeting and sampling average gabbros, in addition to the three-sample averages used in the projections, which have been reasonably successful in reducing, but not eliminating, the scatter in the diagrams. The reasonable correspondence can also be explained where the gabbros are made of mostly included elements and that excluded elements have little effect on bulk-gabbro compositions and the phase diagrams as constructed. Sampling of average gabbros is commonly used for understanding the evolution of layered intrusions as pioneered by Wager (1960).

5.8 Iron-magnesium exchange equilibria

Equilibria between coexisting pyroxenes and olivine can be evaluated by the exchange reaction coefficient for Fe and Mg between olivine and pyroxenes, expressed by the binary K_D calculated as:

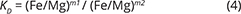
where Fe and Mg are mole fractions, m1 and m2 are coexisting mafic silicates (olivine, clinopyroxene or orthopyroxene), and Fe is calculated as total iron. Fig. 56 shows K_D as a function of stratigraphic height (or generally decreasing temperature) in the LS for three mineral pairs (see also Figs 31, 32). For all pairs, K_D markedly changes at the UZa–UZb boundary, where liquid immiscibility is suggested to commence (see Sections 5.7.7 and 5.12).

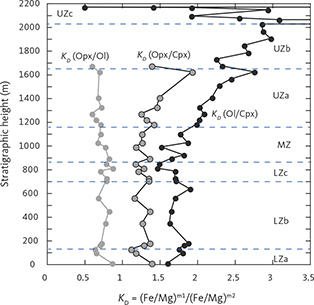
Fig. 56 Calculated partitioning K_D of Fe and Mg for three different pairs of pyroxenes and olivine (Tables 3, 5 and 6) as a function of stratigraphic height (m) in the LS. Calculated using Eq. (4) with all iron as Fe²⁺.

Until the MZ, the olivine-clinopyroxene pair shows a constant K_D of 1.73 ± 0.11 (n = 14), after which K_D systematically increases to c. 3 until reaching UZc, where the observed values are highly variable (Fig. 56). The marked increase in K_D with decreasing T was also observed by Loucks (1996), reaching well above 2 for temperatures below 1000°C. These values are comparable to the experimental determinations of Thy et al. (2006), suggesting K_D = 1.41 ± 0.29 (n = 40) for temperatures above 1080°C (Fig. 57). There is thus an indication of exponential increase in K_D with increasing Fe and decreasing temperature (Fig. 57A).

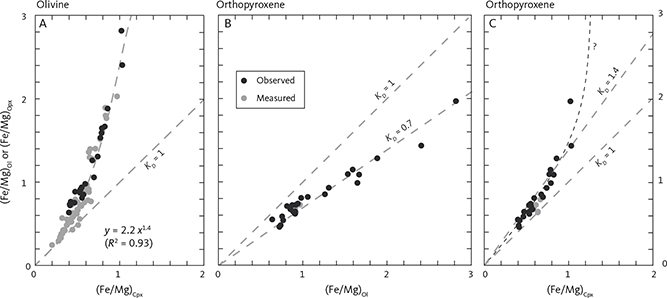
Fig. 57 Co-variation of Fe/Mg ratios for observed orthopyroxenes and olivine (Table 3, 5 and 6) together with the results for one-atmospheric melting experiments (measured; Thy et al. 2006). All iron has been calculated as Fe²⁺. A: (Fe/Mg)_Ol (olivine) vs. (Fe/Mg)_Opx (clinopyroxene) pairs. The Fe/Mg ratio can be fitted to the power equation shown, suggesting K_D values between 1 and 2.5. B: (Fe/Mg)_Opx (orthopyroxene) vs. (Fe/Mg)_Ol pairs. The data can be fitted to a linear equation giving K_D = 0.7. C: (Fe/Mg)_Opx vs. (Fe/Mg)_Opx pairs. The data can be fitted to a linear equation giving K_D = 1.4, although a power equation is a possibility (curve marked ‘?’).

The orthopyroxene-olivine pair shows a constant K_D = 0.73 ± 0.08 (n = 24) until orthopyroxene ceases to crystallise in the UZb (Fig. 57B). This K_D is similar to the experimental K_D = 0.74 ± 0.03 (n = 4) obtained by Thy et al. (2006) for the Skaergaard dykes. These latter results, however, contrast with experimental results by Medaris (1969) and observations for the Bushveld Complex and Stillwater Complex (Atkins 1969; Raedeke & McCallum 1984; Barnes & Naldrett 1986) typically indicating values of c. 0.9–1.0 (Fig. 57B). This difference may be an effect of the relatively evolved iron-rich Skaergaard melts compared to the more mafic compositions of the other layered intrusions. The important observation is that there is a good correspondence between the observed K_D and the experimentally derived K_D for the Skaergaard intrusion (Fig. 57B).

The orthopyroxene-clinopyroxene pair suggests constant partition until the UZa with an average K_D of 1.33 ± 0.16 (n = 24), followed by a slight increase in UZa (Fig. 57C). The K_D for pyroxenes from layered intrusions varies between 1.40 and 1.28 (Brown et al. 1957; McCallum 1968; Atkins 1969; Saxena 1973; Fleet 1974; Barnes & Naldrett 1986), similar to the values for Skaergaard K_D observed here. These values are higher than most of the experimental determinations of Thy et al. (2006) for Skaergaard dykes (K_D = 1.12 ± 0.10 (n = 6) as well as the test for equilibrium of Putirka (2008, p. 95; K_D = 1.09 ± 0.14; Fig. 57C). Again, there is some indication of an exponential increase in K_D with increasing Fe and decreasing temperature, similar to, but less prominent than, in the relationship between the olivine and clinopyroxene pair. The reason for the moderate, but distinct, difference between observed and measured experimental results is not clear, although the results may mostly be within the experimental and analytical uncertainty.

The graphical pyroxene thermometer of Lindsley & Andersen (1983) indicates consistent temperatures for the average clinopyroxene compositions (Fig. 58) suggesting that the compositions obtained in this study, using a broad-beam electron microprobe technique, have reasonably captured the solidus compositions for clinopyroxene. This is also supported by the good match to values obtained by previous studies (Brown et al. 1957; Brown & Vincent 1963) based on mineral separates (Fig. 19) as well as the general lack of strong subsolidus and hydrothermal imprints on the average clinopyroxene compositions (Nwe 1975, 1976; Manning & Bird 1986).

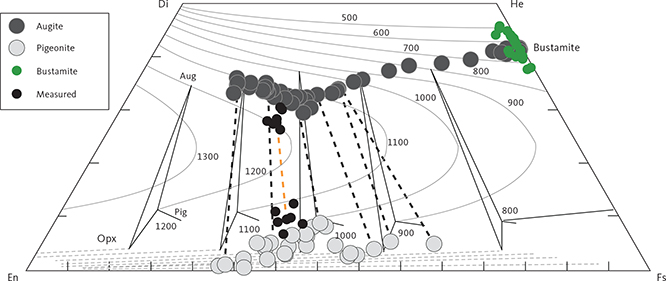
Fig. 58 Pyroxene quaternary diagram with phase equilibria (thin black lines) and temperature contours (solid and dashed grey lines) after Lindsley & Andersen (1983). The pyroxene compositions of Tables 3 and 5 calculated according to Lindsley & Andersen (1983) reduce the pyroxenes to their quadrilateral En–Di–He–Fs components and take all iron to be calculated as Fe²⁺. Black dashed tie-lines are shown for representative Skaergaard pyroxenes. Orange dashed tie-line is for the experimentally determined, average coexisting pyroxenes. Bustamite (inverted ferrobustamite) of UZc from Table 7 is shown for comparison. Di: diopside. He: hedebergite. En: enstatite. Fs: ferrosilite. Opx: orthopyroxene. Pi: pigeonite. Aug: augite.

In contrast, orthopyroxene often suggests much lower equilibrium temperature than for clinopyroxene by up to 100ºC (Fig. 58). The exception is at the MZ–UZa transition, where coexisting pyroxenes appear to approach equilibrium and better match solidus relations (compare Figs 19 and 58). This suggests that the majority of the Skaergaard orthopyroxene compositions may record a strong component of subsolidus equilibration caused by exsolution and grain coarsening, consistent with the phase equilibria considerations (see Section 5.7.5).

The effect of solidus to subsolidus equilibration for the pyroxenes is expected to increase the Fe/Mg ratio of orthopyroxene and decrease the ratio for clinopyroxene. This leads to an anticlockwise rotation of the tie lines for coexisting pyroxenes in the quaternary (see Coleman 1978) and eventual widening of the solvus (Lindsley 1983). A comparison between the coexisting pyroxenes obtained in melting experiments (small filled circles in Fig. 58) and Skaergaard gabbros (large circles in Fig. 58) shows the expected widening of the pyroxene gap for the cumulates with decreasing temperature. Also, despite nearly identical pigeonite-saturation temperature for the gabbro primocrysts (c. 1090°C) and experiments (c. 1084°C), higher pyroxene Fe/Mg ratios are suggested by the experiments than are observed for primocrysts. Further, there is a clear mismatch between the observations and the contours drawn by Lindsley & Andersen (1983).

It is often assumed that the Fe/Mg ratios for equilibrated pyroxenes define a K_D approaching 1.0 (Coleman 1978; Putirka 2008). In Fig. 58, this would mean that the tie lines for high and low Ca pyroxenes would extrapolate to a point close to the wollastonite apex. However, for the Skaergaard intrusion, this does not appear to be the case. Rather, the tie lines for the experimental pyroxene pairs extrapolate to a Ca/Mg ratio of c. 2.7 similar to the orientation of tie lines for gabbro rocks with similar pyroxene Mg numbers. This suggests that values of K_D for the coexisting pyroxenes in highly evolved basaltic melts are dependent on temperature and composition. In summary, despite these differences, the consistency of Fe-Mg exchange in the experiments on Skaergaard-like liquids and gabbroic rocks suggest that the pyroxenes in the gabbros are well equilibrated, albeit at subsolidus conditions.

5.9 Magmatic volatiles

Although the initial Skaergaard magma is considered to have been virtually dry, evidence of volatile components (H,Cl,F,S) is captured by apatite, sulphides and hydrous silicates in the gabbros, particularly after advanced degrees of crystallisation. Assuming an initial volatile content equivalent to basalts from the Galapagos spreading centre (H₂O = 0.09%, Cl = 0.08%, F = 0.02%, S = 0.12%; Byers et al. 1984; Michael & Chase 1987), and assuming perfect fractional crystallisation, we can estimate the concentrations of volatile components at the beginning of UZb and at the onset of liquid immiscibility. Using a trapped-liquid content of 2.5% (Tegner et al. 2009), the volatile content can be calculated as H₂O = 0.71 wt%, Cl = 0.24 wt%, F = 0.08 wt% and S = 0.56 wt%. These values are taken to represent the end-member estimates at the UZa–UZb boundary, as well as for an equivalent interstitial-melt evolution below this boundary.

The estimates for H₂O are well below saturation for basaltic and ferrobasaltic magmas and the precipitation of amphibole and biotite (Burnham 1975; Berndt et al. 2005; Shishkina et al. 2010). However, the modelled H₂O content (0.36–0.71) may have been sufficiently high to result in detectable effects on the mineralogy and crystallisation temperatures in at least the MZ to UZa (Berndt et al. 2005; Botcharnikov et al. 2008). The experimental calibration of Almeev et al. (2007, 2012) predicts that in the upper part of UZa, the liquidus depression for olivine may have reached 15–30°C, depending on the trapped-melt model, and 35–60°C for plagioclase at the top of the UZa, relative to the dry liquidus. The experiments of Almeev et al. (2007, 2012) were performed on typical MORB composition and an applied pressure of 200 MPa. The relatively strong depression suggested for the plagioclase liquidus would markedly have modified the melt evolution and equilibrium compositions of plagioclase in the upper parts of the intrusion, while similar effects on olivine saturation would not have been as marked as for plagioclase. A small H₂O content may also have raised the temperature of the onset of liquid immiscibility (cf. Lester et al. 2013) and may partially explain the inferred high temperature of immiscibility for the Skaergaard (see Section 5.7.7). However, the effects of wet (or damp) crystallisation have so far eluded experimental and forward modelling of the Skaergaard intrusion, which have exclusively been modelled assuming dry conditions (Toplis & Carroll 1996; Thy et al. 2006). The reason for this is the lack of applicable experimental calibrations and information on melt composition.

Biotite, intermediate between phlogopite and annite (Fig. 24), occurs as a minor interstitial and late-crystallising mineral together with ilmenite and apatite (Fig. 6). This hydrous silicate was considered by Nash (1976) to have been secondary, subsolidus reaction products, involving a residual magmatic fluid. Hydrothermal, mineralised fracture veins are also abundant in the intrusion (Bird et al. 1986, 1988), some of which contain biotite of a similar composition to those of this study. Nash (1976) interpreted the fluorine and H₂O partitioning between apatite and biotite to suggest that biotite had lost fluorine to a circulating meteoric fluid, while apatite had retained the magmatic fluorine content. However, using the analytical results of Nash (1976) as well as Sallet’s (2000) solution to the partitioning of fluorine between coexisting biotite and apatite, an approximate equilibrium temperature of 920°C is suggested. This may be a reasonable estimate of near-solidus temperature, above most of the subsolidus temperatures, based on the FeTi oxide thermometry. However, it ignores the substantial amount of chlorine in apatite (Table 10). The appearance of magmatic biotite, confined to the LZ and into the base of the MZ, is attributed to a channelled influx of water into parts of the early mush in approximate contact to the host, metamorphic basement. Such an influx could have resulted in sufficiently raised local H₂O concentrations to saturate biotite without reaching H₂O saturation and fluid development. Pegmatitic gabbros in the LZ contain trapped fluid inclusions with H₂O and CH₄, suggesting that the final evolved interstitial melt and the SH alike may have coexisted with a hydrous fluid similar to that trapped in the minerals at T < 770°C (Larsen et al. 1992; Sonnenthal 1992; Larsen & Brooks 1994).

The monovalent anions in apatite suggest a two-step boiling point. First as a loss of chlorine in the UZb, where apatite becomes an early-forming mineral, and liquid immiscibility reaches the liquidus, and again in UZc, when apatite essentially becomes dry by losing OH (Fig. 24B). McBirney (1995, 2002) and Sonnenthal (1992) observed an increase in the F/Cl ratio of apatite from the beginning of the upper part of MZ and culminating at the SH (or slightly above), which they attributed to the development and removal of chlorine with a hydrous fluid vapor (cf. Doherty et al. 2013). They also suggested that the upward concentration of excluded trace elements near the top of the intrusion was caused by a gradual change in the partition coefficient in response to the exsolution of a volatile fluid. This formation of a Cl-rich and volatile-rich fluid may have influenced the development of the mineralisation in the upper part of the MZ (Boudreau & McCallum 1992). Detailed petrographic and geochemical studies have partly confirmed this expectation and argue that the formation of Au-rich sulphides in the topmost part of the mineralisation was associated with a Cl-bearing aqueous fluid (Godel et al. 2014; Nielsen et al. 2015; Rudashevsky et al. 2023). Sulphide liquid immiscibility occurred when the liquid sulphur content reached 0.26 wt% in the upper part of the MZ according to Andersen (2006), compared to our estimate of 0.22–0.16 wt% at approximately the same level. This saturation resulted in strong concentrations of the Au and PGEs in a narrow zone in the upper part of the MZ (Triple Group; Andersen et al. 1998), although this interpretation is controversial (Bird et al. 1991; Andersen et al. 1998; Andersen 2006; Godel et al. 2014; Keays & Tegner 2015; Nielsen et al. 2015, 2019b; Holwell et al. 2016; Pedersen et al. 2020).

The presence and the effects of volatile components on the fractionation history of the Skaergaard intrusion are poorly understood, although evidence points towards the precipitation of hydrous silicates and to the separation of fluid vapours from the melt in the upper part of the intrusion. Future studies should focus on volatile components as well as experiments and modelling of their effects on the liquid lines of descent and trace element partitioning to expand our understanding of the potential importance of volatiles, particularly for the late stages of solidification.

5.10 Kinematic and thermal constraints

An evaluation of the dynamic behaviour of melt and primocrysts is indicative for understanding processes forming the mush and its final solidification mechanisms. The density relations of the mush system can be calculated for both primocrysts and coexisting melt using partial molar volumes (Bottinga & Weill 1970; Bottinga et al. 1982; Lange & Carmichael 1987, 1990; Knoche et al. 1995). The densities of the primocrysts and crystal network are calculated here using the thermal expansion equations of Niu & Batiza (1991a, b), taking into consideration the mineral composition, liquidus temperature and observed mineral modes. The single mineral and crystal network-density calculations are shown in Fig. 59A.

The calculated density of the crystal network can be compared to the specific gabbro density measured relative to water using Archimedes’ principle (Fig. 59A). The measured densities, although matching the observed densities, are slightly lower, presumably because the former is affected by cracking at ambient temperatures (Tegner et al. 2009).

The composition of the coexisting melt is not directly known. However, density calculations using the two end-member modelled liquid lines of descent are reasonable predictions of the possible ranges in density (Tables 21, 22). The calculation results are compared in Figs 59A and 59B, showing the two liquid lines of descent and the effects of a small amount of water amounting to an initial 0.10 wt% (see discussion on magmatic volatiles in Section 5.9).

The primocrysts group into low-density plagioclase (c. 2.6–2.7 g·cm⁻³), medium-density mafic silicate minerals (3.4–4.0 g·cm⁻³) and high-density FeTi oxide minerals (3.7–4.9 g·cm⁻³; Fig. 59A). Of the primocrysts, only olivine suggests a strong increase in density with stratigraphy, reaching a difference of 0.7 g·cm⁻³ from the base to the top in the intrusion, thus recording the upward increasing fayalite. The density of the coexisting melt is predicted to be very similar to, or narrowly parallels, that of plagioclase (Fig. 59A). The difference between plagioclase primocryst and melt densities varies for the Si-enriched liquid line of descent from –0.15 to +0.15 g·cm⁻³ with the neutral crossover in the middle of UZa, a potential buoyancy of plagioclase in the lower part of the intrusion and an accumulation in the upper part of the intrusion (Fig. 59A). For the Fe-enriched liquid line of descent, the liquid is systematically higher by 0.13–0.17 g·cm⁻³ throughout the intrusion, suggesting plagioclase buoyancy throughout the LS. The effect of water as well as a high trapped-liquid content are minimal until about the UZb (Fig. 59B), where liquid immiscibility appears on the liquidus and the density calculations that use the liquid lines of descent based on fractional crystallisation may have less practical relevance.

The viscosity of a magmatic melt is a measure of its internal resistance to flow, the tendency for primocryst migration in the magma and for melt migration in the mush network. Dynamic viscosity is measured as the ratio of the shear stress to the time rate of shear strain, is dependent on temperature and composition, and in particular, on the silica melt content or melt polymerisation. The viscosity has been directly determined experimentally in complex and simplified systems using rotational or falling sphere viscometers (e.g. Ryan & Blevins 1987). Such experimental results have been used by Bottinga & Weill (1972), Shaw (1972) and Giordano et al. (2008) to formulate equations for the temperature and compositional dependency of viscosity for complex silicate melts. The results of the viscosity calculations for the Skaergaard liquid lines of descent, using the procedure of Giordano et al. (2008), are shown in Fig. 59C. For the Si-enrichment trend with increasing silica content, the viscosity shows an increase from 1.8 to 6.2 – on a logarithmic scale in Fig. 59C – but a more restricted variation for the Fe-enrichment trend of 1.8 to 3.4 – again on a logarithmic scale. For the former, this is equivalent to 90 Pa·s at the base of LZa, to 71 000 Pa·s at the base of UZb. Multiply by 10 to convert these viscosities to the traditionally used poise unit based on g·cm^–1·s^–1. Water systematically lowers the viscosity by 9–18% on the logarithmic scale.

Stokes equation relates the contrast between viscosity and density to the settling velocity of primocrysts in a stagnant or slowly convecting magma as:

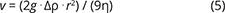
where v is the terminal settling velocity (m·s^–1), g is the gravitational acceleration (9.8 m·s^–2), Δρ, either positive or negative, and is the density contrast between the primocryst and the melt (kg·m^–3), r is the radius of a spherical primocryst (m), and η is the dynamic viscosity (Pa·s). This equation allows us to calculate the settling or flotation rate and thus the separation of primocrysts in melts of known or assumed densities and viscosities.

Using Stokes equation, Eq. (5), the settling or flotation rate for plagioclase grains (of a constant 1 mm radius) in a stagnant anhydrous melt of the LZa is about 30 m·y^–1 and markedly decreased upward to approach zero at the base of the UZa or slightly negative values above (Fig. 59D). The other main silicate primocrysts (olivine and pyroxene), assuming a similar size, will settle with a rate of 98–132 m·y^–1 and again will become stagnant at UZb. The gabbro rate is calculated assuming a clustered settling that represents the observed average gabbro mode and its variation. All these calculated settling rates are normalised to a unifying particle of 2 mm in diameter. For the Si-enriched liquid line of descent, the gabbro settling rate is 43 m·y^–1 in LZa reaching near zero in UZb. Using the Fe-enrichment descent will slightly increase this rate to 51 m·y^–1 in LZa and, because of the more restricted silica enrichment in the upper part of the intrusion, will stabilise in UZa only at a rate of <10 m·y^–1. Water approximately doubles the settling velocity in the LZ, caused mainly by the break-up of silicate melt polymerisation and thus the reduction in viscosity.

The total settling times for clustered gabbro accumulation, integrated from the velocity data shown in Fig. 59D, suggest fast accumulation in the lower part of the intrusion (LZ–UZa) of 307 years (an average of 3.7 m·y^–1) and for the whole intrusion of 4130 years (an average of m·y^–1). These accumulation times apply to the Si-enrichment liquid line of descent. As expected, they only increase if the Fe-enrichment liquid line of descent is considered (an average of 13 m·y^–1) and similarly for wet conditions (18–34 m·y^–1).

These settling durations are several orders of magnitudes faster than rates estimated for the Skaergaard intrusion from thermal heat-transfer modelling (Wager & Brown 1967, p. 210; Irvine 1970b; Norton & Taylor 1979). The thermal models assume heat loss mainly through the roof and adiabatic convection in the melt and incorporate temperature contrasts between magma and the host, specific heat content and density, thermal conductivities and latent heat of crystallisation. The modelling of Norton & Taylor (1979, fig. 10) suggested a duration of 130 000 years to reach the solidus temperature (or F = 0) and 80 000 years to reach UZb or a temperature of about 1060°C (F = 0.25). Other estimates, orders of magnitude lower, have been proposed by Wager & Brown (1967, p. 210) who used a constant accumulation rate of 0.20 m·y^–1 based on the modelling of the Stillwater Complex by Hess (1960) and thus suggested 12 000 years for the entire LS and an inferred 8000 years to reach the UZb. The “basic model”, incorporating the development of an UBS, as formulated by Irvine (1970b, fig. 10), suggests an upward accumulation rate of approximately 11 m·y^–1 and thus a total time of 40 000 years for the entire LS and 22 000 years to reach the UZb – significantly less than the estimates of Norton & Taylor (1979). The apparent low estimate by Wager & Brown (1967) is due to not incorporating a UBS that significantly reduces the heat loss from the roof of the intrusion (Irvine 1970b; Irvine 1974). Similar cooling estimates for the Bushveld Complex, to about the same minimum temperature as used in Irvine’s calculations (1970b), suggest accumulation rates of 0.04–0.05 m·y^–1 (Cawthorn & Walraven 1998; Zeh et al. 2015).

The use of Stokes equation assumes spherical particles in an infinite, non-convecting media without interaction with other particles to calculate the steady-state terminal velocities. Thus, the modelling probably has limited applications to the Skaergaard crystallising chamber. Specifically, the calculations are normalised to unified-sized particles and non-spherical particle shapes, and particle interactions in the multi-saturated melt are certainly plausible. Further, the gabbro clustering in question probably cannot be reduced to mm-sized spherical composite particles but would more likely involve solid porous-particle settling in a melt. Such factors may thus greatly reduce the settling velocity by as much as 100 times (Irvine 1974) than the ideal conditions shown in Fig. 59D. Furthermore, adiabatic convection in the main magma chamber may cause delay or retention of crystals (Marsh & Maxey 1985; Marsh 1988; Martin & Nokes 1989) – particularly in high viscosity melts like the upper part of the Skaergaard intrusion, but less so in the lower parts where settling velocities may have been higher.

Despite such uncertainties and limitations in the application of Stokes equation to magma chambers, the normalised settling rates of Fig. 59D suggest that crystal settling might have operated in the lower part (i.e. LZ) of the intrusion and is unlikely to have had any effect in the upper parts (i.e. MZ and UZ). There is also no strong indication of plagioclase flotation, although stagnation may have been in operation (cf. Maaløe 1984).

The possible effects of liquid immiscibility can be evaluated using the experimental results of Charlier & Grove (2012). Calculated on a dry basis, the two conjugate immiscible melts have densities with differences of about 0.50 g·cm^–3 (Fig. 59B), probably sufficient to result in liquidus separation of these two melts. Further, the contrast in the dry viscosity for the two conjugate liquids is high with 270 Pa·s for the Fe melt and 54 000 Pa·s for Si melt (Fig. 59C). The separation velocity for the two melts is thus well over 100 m·y^–1, based on a settling velocity of 112 m·y^–1 for the Si-rich cognate melt and 0.6 m·y^–1 for the Fe-rich melt. This suggests the cognate immiscible melts might have been able to efficiently separate with the Si-rich melt floating upward and the Fe-rich melt sinking or remaining stagnant at the base of UZb.

The surface tension (gas-melt) of the two individual conjugate immiscible melts can be estimated by the addition of the partial molar tensions at 1500°C using the procedure of Mills (1986). The results adjusted to a temperature of 1060°C, as estimated for immiscibility in the fractionating Skaergaard melt, by using the dependence determined by Walker & Mullins (1981), is for the Fe-rich melt 265 ± 2 dyn·cm^–1 (equivalent to mN·m^–1) and for the Si-rich melt 173 ± 9 dyn·cm^-1. The procedure of Kucuk et al. (1999), adjusted as above from a temperature of 1400°C, suggests 346 ± 1 dyn·cm^-1 and 301 ± 5 dyn·cm^-1, respectively. These are within the range of the experimental results obtained on a variety of basaltic and andesitic melts by Walker & Mullins (1981), by Veksler et al. (2010) for the simplified K₂O-FeO-Fe₂O₃-Al₂O₃-SiO₂ system, and by Murase & McBirney (1973) on basalts to rhyolites as read from their graph at an extrapolated temperature of 1060°C. The results indicate similar surface tensions with the Fe-rich immiscible melt slightly higher than for the Si-rich melt.

Based on these individual estimated values, we can calculate a dry interfacial tension (melt-melt) of 2–10 dyn·cm^-1 between the two conjugate melts by using the solution of Girifalco & Good (1957) and the simplification suggested by Veksler et al. (2010). This is a low interfacial tension, but not very different to those directly measured by Veksler et al. (2010) at 8–16 dyn·cm^-1 for corresponding immiscible melts in the K₂O-FeO-Fe₂O₃-Al₂O₃-SiO₂ system. Veksler et al. (2010) further speculated that the interfacial tension in natural basaltic melts would be 2 or 3 times lower than observed in their simplified system, or in other words corresponding to what is estimated here.

Such a low interfacial tension would have resulted in enhanced nucleation in the case of Fe-rich melt droplets in a continuous Si-rich melt (Charlier & Grove 2012; Honour et al. 2019a). Another effect would be to slow coarsening by ripening and coalescence of the droplets, which would result in a protracted stability of the emulsion and hence restrict early gravitative separation of the immiscible melts (Veksler & Charlier 2015). The latter appears to contrast with the evidence for large-scale gravitative separation of the emulsion in the UZb suggested for the Skaergaard intrusion (see Section 5.12). This may, however, be an apparent rather than a real conflict, since the time duration for UZb–UZc to solidify has variably been estimated to thousands of years (e.g. Norton & Taylor 1979). Such long timespans may have allowed near complete coarsening of melt droplets (James 1975) and thus allow sufficient time for breakdown of any initial emulsions and the effective separation of the two immiscible melts.

Although interfacial tension may be relevant for understanding the fluid-dynamic behaviour of the immiscible melts in the residual melt chamber, it is less significant when considering what is happening in the trapped melt in the mush zone where solid-melt interactions with primocrysts (or wetting properties) may in part control the relative migrations of the two immiscible melts in highly heterogeneous, but poorly understood mush pathways (Honour 2019; Honour et al. 2019b; Holness et al. 2020).

5.11 Forward modelling of trace elements

The vast amount of field data, petrographic data and compositional data for the Skaergaard lends itself to more rigorous testing of liquid line of descent models. We have already discussed the modelling of the major elements (see Sections 5.5–5.8). Here we continue by examining the trace elements to evaluate various reference fractionation models.

The elemental concentrations of the gabbros (Tables 1, 16) represent a mixture of primocrysts and trapped interstitial (or mesostasis) material (Wager 1963; Henderson 1970, 1975). The calculated mineral modes in Table 2 are based on these bulk-gabbro compositions, which include only primocrysts and are without a component of trapped melt. The results may thus only represent a first order approximation to the primocryst mineral modes. This may, nevertheless, be a reasonable approximation given that the trapped melt typically appears to be restricted (Tegner et al. 2009) and may have crystallised without significant migration and melt fractionation. The excluded trace elements are confined to late-formed minerals but may also be present in small amounts in the primocrysts. An example, which is often used to calculate the trapped melt content, is Rb that may reside in minute and late-crystallised orthoclase, but also enters plagioclase in small amounts. This may result in a bulk-partitioning coefficient for Rb in the MZ of around 0.14 (see Section 5.11.3).

Our modelling is based on the bulk-gabbro compositions and experimentally known partitioning. First, we evaluate the mineral-melt partitioning (D_i), then the bulk partitioning (D_i^*), and then the effects of trapped-melt component (F_TM). We then show that in some cases reference fractionation models fail to fully account for the observations and we are consequently steered in new directions, sometimes still without satisfactorily solving the problem at hand. We begin with some basic constraints on element partitioning followed by forwarding modelling of the trace element variations.

5.11.1 Calculation methods

The trace element partition (D_i) between coexisting solid mineral and liquid is defined on a weight basis as:

where D_i is the Nernst partition coefficient and C_i is the concentration of an element i, respectively, in mineral (m) and liquid (l).

The bulk partition coefficient (D_i^*) between the solid and the liquid for an element i for j = 1 to n can be defined as:

or by inserting Eq. (6) into Eq. (7), for j = 1 to n, we obtain:

where m_i^j is the modal weight fraction of a specific mineral j and a specific element i, D_i^j is the elemental partition coefficient of Eq. (6) for the same mineral j, and n is the total number of minerals (or components) in the gabbro rock. The modal weight fractions (m_i) vary individually from 0 to 1, and total 1.

The D_i^* can be estimated for many elements because the modal solid mineral fractions are known (Table 2; Fig. 15) and the individual elemental partition coefficients can be reasonably estimated using existing experimental data (e.g. Nielsen 1992). Equations (7) and (8) can be expanded to n + 1 by adding an interstitial trapped-melt component with D_i = 1, treating the trapped-melt component like a mineral and assuming little or no migration of melt. Calculated this way, D^* represents the crystal mush, incorporating a trapped-melt fraction that theoretically can vary from zero to 1. Elements with D^* > 1 are defined as included in the bulk mush (compatible), while elements with D^* < 1 are defined as excluded from the mush zone (incompatible) but included in the residual melt.

The residual (or inverted) liquid concentration (C_i^l) can be obtained by inversion because the D_i^* and gabbro mush concentration are known. Thus, the equilibrium concentration of a trace element in the liquid can be predicted using the bulk partition coefficient from Eq. (8) and the gabbro concentration, resulting in:

where C_i^mush is the measured concentration of the element i in the gabbro. Only for D_i^* = 1 is C_i^l equal to C_i^mush; describing perhaps a hypothetical end-condition where the mush is made up of 100% ‘trapped’ melt.

Perfect fractional crystallisation can, if F is known, be calculated stepwise as C_i^l / C_i^o using the batch equilibrium-crystallisation equation,

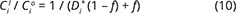
or by the Rayleigh distillation equation,

where C_i^l is the resultant concentration and C_i^o is the previous melt composition for individual steps, D_i^* is constant for an individual step, and f is the ratio between F (here the liquid-fraction remaining) for the resultant and F for the previous melt segment. F for perfect fractional crystallisation can be estimated from the stratigraphic height using the method of Tegner et al. (2009) in Eq. (1). If the initial concentration of an element i is known or can be constrained otherwise, C_i^l can thus be calculated for each step from Eqs (10) or (11).

Equilibrium crystallisation can be approximated using Eq. (9), assuming that C_i^mush is constant for each step and equal to the initial melt composition, and not variable as for perfect fractional crystallisation. The equilibrium variation is constrained by the bulk partition coefficient, the modal make-up of the gabbros, and ultimately the temperature and the initial concentration. Equilibrium crystallisation is specifically of interest for evaluating the effects of imperfect fractional crystallisation that can be calculated as a mixture of fractional and equilibrium crystallisation. Used this way, ‘imperfect’ does not refer to disequilibrium distributions of the trace elements.

The fraction of trapped melt (F_TM) in the gabbros for each step can be estimated using an excluded element (i) as:

where C_i^l is the predicted concentration of element i in the liquid using Eq. (10) or (11) and C_i^mush is the measured gabbro or mush concentration of the same element. F_TMapproaches an ideal value as D_i^* → 0. Using Eq. (11) or (12) based on the assumption of perfect Rayleigh fractionation, Tegner et al. (2009) calculated the Skaergaard trapped-melt fractions using the gabbro concentrations for Rb or U throughout the LS. Similar calculations are iteratively done here assuming stepwise D_i^*-values initially without a priori incorporating a trapped-melt content.

In situ crystallisation can, following Langmuir (1989), be modelled as

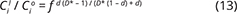
where C, f, and D^* are defined previously and d is the fraction of melt in the boundary zone returned to the main chamber. The boundary zone where crystallisation occurs can be viewed as the sum of the fractions of solid, trapped liquid, and the fraction of the returned liquid, such that d is equal to one minus the combined solid fraction and F_TM. Eq. (13) is similar to the equation by Langmuir (1989) for the case without trapped melt and is applicable here because D^* incorporates the trapped melt component and, argues Langmuir (1989), approximates the partitioning between the returned melt and the original melt. The limiting values of d = 1 correspond to perfect fractional crystallisation, while d = 0 equates to equilibrium crystallisation. The trapped melt fraction is known and the solid fraction of the crystallising boundary zone can be bracketed, or estimated, to be between 0 and 1 with a reasonable constant average of 0.5, assuming a linear variation from base to top as suggested by Langmuir (1989).

5.11.2 Mineral-liquid partition coefficients (D)

The partitioning of the elements Sc, V, Cr, Co, Ni, Zn, Rb, Sr, Y, Zr, Nb, Ba, La, Yb and U has been evaluated for olivine, plagioclase, pyroxenes, FeTi oxides and apatite, using the experimentally determined mineral-liquid partition coefficients (D) reported by Nielsen (1992) as a FORTRAN code taking into account the dependency on temperature, melt composition, and some aspects of mineral composition. The lattice-compensated strain model of Blundy & Wood (1994), as formulated by Bédard (2005, 2006, 2007, 2014), was used to calculate the partition for the REE together with Y and Sc. Temperature can be estimated from the An content of plagioclase using the method of Thy et al. (2009a, 2013) and the mineral compositions in Tables 3–5. The major element melt compositions are from the forward modelling in Tables 21 and 22, calculated to represent the two contrasting views of Fe depletion and Si enrichment (Hunter & Sparks 1987; Toplis & Carroll 1996) and prolonged Fe enrichment with restricted Si enrichment (McBirney & Naslund 1990; Tegner 1997), both past FeTi oxide crystallisation and both extrapolated to F = 0. The use of the two contrasting liquid lines of descent thus results in two sets of partitioning coefficients. A summary of D values for minerals and subzones is shown in Table 23 where values overlap below the MZ, as expected. One major limitation in these calculations is the uncertainty in the modelled liquid lines of descent, but there also exist uncertainties in the partitioning relations for silica melts in the models of Nielsen (1992) and Bédard (2014) that could become problematic towards the end stages of evolution for strong Si-enrichment models. The main conclusion is that the trace element partitioning depends on temperature as well as melt and mineral compositions. The individual partition coefficients for the prolonged Fe-enrichment model (lower end of the ranges in Table 23) are similar to those obtained by McBirney (1998), who only assumed a melt composition characterised by increasing Fe enrichment beyond FeTi oxides (McBirney & Naslund 1990). As in our modelling, McBirney (1998) also used the source code of Nielsen (1992) for his calculations.

Table 23 Summary of selected single-element and bulk-element partition coefficients

	Sc		V		Cr		Co		Ni		Zn		Rb		Sr		Y		Zr		Nb		Ba		La		Yb		U
Olivine
UZc	1.4–3.3		0.06–0.15		0.58–1.4		2.0–4.7		69–164		1.1–2.7						0.22–0.63										0.42–1.1
UZb	1.4–3.3		0.06–0.11		0.50–0.88		1.9–3.3		57–102		1.1–1.9						0.23–0.64										0.43–1.1
UZa	1.1–1.8		0.05–0.07		0.35–0.48		1.5–2.0		40–54		0.85–1.1						0.17–0.33										0.33–0.59
MZ	0.60–0.65		0.04–0.05		0.29–0.33		1.3–1.5		33–37		0.74–0.86						0.06–0.06										0.12–0.14
LZc	0.45–0.65		0.04–0.04		0.26–0.28		1.2–1.3		28–31		0.70–0.76						0.04–0.04										0.09–0.10
LZb	0.33–0.49		0.04–0.04		0.22–0.24		1.2–1.2		24–26		0.65–0.69						0.03–0.03										0.06–0.07
LZa	0.27–0.29		0.04–0.04		0.21–0.21		1.1–1.1		22–23		0.63–0.65						0.02–0.02										0.04–0.05
Clinopyroxene
UZc	40–56		0.60–1.42		103–247		2.7–6.5		49–117		0.66–1.6				2.0–4.7		2.0–2.7		0.42–4.3				0.07–0.17		0.39–0.58		1.7–2.2
UZb	15–29		0.49–0.99		66–119		2.6–4.5		36–64		0.62–1.1				1.4–2.5		1.3–1.8		0.31–4.7				0.07–0.12		0.21.0.34		1.1–1.5
UZa	8.0–13		0.45–0.61		33–45		2.1–2.8		22–29		0.49–0.66				0.79–1.1		0.9–1.1		0.13–1.4				0.06–0.07		0.14–0.18		0.86–1.0
MZ	5.6–6.0		0.40–0.46		21–25		1.8–2.1		16–18		0.43–0.50				0.56–0.64		0.73–0.76		0.10–0.16				0.05–0.06		0.10–0.10		0.68–0.71
LZc	5.0–5.2		0.37–0.42		16–18		1.7–1.9		13–14		0.41–0.45				0.45–0.49		0.65–0.67		0.10–0.12				0.04–0.05		0.09–0.09		0.62–0.63
LZb	4.4–4.5		0.35–0.37		11–12		1.6–1.7		10–11		0.38–0.40				0.34–0.36		0.59–0.60		0.11–0.09				0.04–0.05		0.08–0.08		0.57–0.57
LZa	4.0–4.1		0.34–0.35		8.9–8.9		1.5–1.6		8.3–8.5		0.37–0.38				0.27–0.28		0.55–0.55		0.24–0.09				0.04–0.04		0.07–0.07		0.53–0.53
Orthopyroxene
UZc
UZb
UZa	4.3–8.9		0.30–0.40		7.7–10		1.8–2.4		11–14								0.42–0.62								0.06–0.15		0.57–0.79
MZ	1.9–2.2		0.26–0.30		6.2–7.1		1.6–1.8		7.9–8.9								0.24–0.26								0.02–0.02		0.36–0.38
LZc	1.4–1.5		0.24–0.27		5.4–6.0		1.5–1.6		6.4–7.0								0.17–0.19								0.01–0.01		0.26–0.29
LZb	1.0–1.1		0.23–0.25		4.7–5.0		1.4–1.5		5.0–5.3								0.11–0.13								0.00–0.01		0.19–0.21
LZa	0.78–0.83		0.22–0.23		4.2–4.3		1.4–1.4		4.1–4.2								0.09–0.10								0.00–0.00		0.15–0.16
Plagioclase
Uzc	0.09–0.11		0.07–0.17										0.16–0.38		1.5–1.0		0.09–0.09						0.20–0.01		0.18–0.18		0.07–0.07
Uzb	0.09–0.12		0.07–0.12										0.15–0.26		0.24–0.34		0.07–0.07						0.03–0.05		0.16–0.16		0.05–0.05
Uza	0.08–0.10		0.06–0.07										0.12–0.16		0.43–0.87		0.06–0.06						0.08–0.15		0.14–0.14		0.04–0.04
MZ	0.04–0.05		0.05–0.06										0.11–0.12		0.74–0.79		0.05–0.05						0.14–0.15		0.13–0.13		0.04–0.04
LZc	0.02–0.03		0.04–0.05										0.10–0.11		0.74–0.70		0.05–0.05						0.15–0.14		0.12–0.12		0.03–0.03
LZb	0.01–0.01		0.04–0.05										0.09–0.10		0.91–0.67		0.04–0.04						0.20–0.15		0.11–0.11		0.03–0.03
LZa	0.00–0–00		0.04–0.04										0.09–0.09		1.5–0.76		0.04–0.04						0.37–0.18		0.10–0.10		0.02–0.03
Magnetite
UZc		4.2–4.5		44–105		753–1790		13–30		21–51		19–46								0.07–0.19		0.09–0.22
UZb		4.2–4.5		41–73		626–1111		12–21		19–34		18–32								0.07–0.19		0.09–0.22
UZa		3.9–4.2		33–45		435–585		9.6–13		15–20		14–19								0.07–0.19		0.09–0.22
MZ		3.0–3.2		29–34		347–399		8.2–9.7		12–14		13–15								0.04–0.09		0.06–0.11
LZc		2.3–2.5		27–30		304–335		7.9–8.7		11–13		12–13								0.03–0.05		0.04–0.06
LZb		1.5–1.7		26–27		261–277		7.4–7.9		10–11		11–12								0.04–0.04		0.05–0.05
LZa		1.0–1.1		25–26		233–241		7.1–7.4		9.7–10		11–11								0.14–0.04		0.16–0.05
Ilmenite
UZc		16–18		20–47		44–104		2.4–5.8		18–43								0.50–0.56		11–26		27–63				0.39–0.54		0.51–0.56
UZb		16–18		19–33		41–73		2.3–4.0		17–30								0.50–0.56		10–18		25–44				0.40–0.54		0.52–0.56
UZa		14–15		15–20		33–45		1.8–2.5		14–18								0.46–0.49		8.2–11		20–27				0.32–0.40		0.48–0.51
MZ		9.2–10		13–15		29–34		1.6–1.9		12–14								0.31–0.33		7.2–8.3		18–20				0.11–0.14		0.36–0.38
LZc		6.2–7.1		12–13		27–30		1.5–1.7		11–12								0.22–0.25		6.7–7.4		17–18				0.04–0.06		0.28–0.30
LZb		3.1–3.9		12–12		26–27		1.4–1.5		10–11								0.12–0.14		6.3–6.7		16–17				0.01–0.02		0.17–0.20
LZa		1.5–2.0		11–11		25–26		1.4–1.4		10–10								0.06–0.08		6.1–6.3		15–16				0.00–0.00		0.10–0.13
Apatite
UZc		0.22–0.59								0.81–1.9						2.1–5.0		14–53		0.51–1.2						9.1–34		7.2–37		0.80–1.9
UZb		0.22–0.42								0.76–1.3						2.0–3.5		13–34		0.48–0.84						8.4–24		6.6–22		0.75–1.3
UZa		0.18–0.23								0.61–0.82						1.6–2.1		10–17		0.38–0.52						6.8–12		5.3–9.6		0.60–0.81
MZ		0.08–0.09								0.53–0.61						1.4–1.6		8.8–11		0.34–0.39						6.1–7.2		4.4–5.6		0.53–0.61
LZc		0.04–0.05								0.50–0.55						1.3–1.4		8.0–8.7		0.32–0.35						5.7–6.1		3.9–4.4		0.49–0.54
LZb		0.03–0.03								0.47–0.50						1.2–1.3		7.2–7.3		0.30–0.31						5.3–5.4		3.5–3.6		0.46–0.49
LZa		0.03–0.03								0.45–0.47						1.2–1.2		6.8–7.0		0.29–0.30						5.1–5.3		3.3–3.4		0.45–0.46
Bulk partition coefficients based on mineral modes in Table 2 and trapped melt by Tegner et al. (2009)
UZc		15–21		1.2–2.8		38–91		1.5–3.5		31–76		0.46–1.1		0.09–0.16		1.3–1.8		1.0–1.9		1.2–3.3		1.3–3.2		0.49–0.47		0.36–0.81		0.93–1.7		0.19–0.23
UZb		5.0–8.6		2.1–3.6		29–50		1.4–2.4		22–39		0.73–1.2		0.09–0.14		0.50–0.85		0.90–1.8		0.76–2.2		1.6–2.8		0.05–0.08		0.48–1.1		0.67–1.4		0.06–0.10
UZa		4.0–5.8		2.8–3.7		31–41		1.4–1.8		31–41		0.87–1.1		0.12–0.14		0.49–0.76		0.46–0.55		0.76–1.4		1.7–2.3		0.12–0.15		0.21–0.24		0.43–0.52		0.08–0.09
MZ		3.2–3.5		3.4–3.9		28–32		1.4–1.6		11–15		0.89–1.0		0.14		0.52–0.60		0.39–0.41		1.1–1.2		2.4–2.8		0.16–0.17		0.19–0.20		0.38–0.40		0.11
LZc		2.6–2.8		3.3–3.7		25–27		1.3–1.5		7.4–8.1		0.89–1.0		0.16		0.48–0.49		0.38–0.39		1.1–1.2		2.4–2.6		0.13		0.21		0.38–0.39		0.14
LZb		1.3–1.4		0.77–0.80		6.2–5.6		0.82–0.86		4.1–4.4		0.4		0.24–0.25		0.66–0.56		0.37–0.38		0.34		0.47–0.49		0.29–0.27		0.28		0.36–0.37		0.21
LZa		0.86–0.81		0.77–0.89		3.8–3.9		0.80–0.55		3.2–3.9		0.5		0.38		0.92–0.64		0.44		0.47–0.45		0.57		0.48–0.41		0.40		0.43–0.44		0.35
Calculated using Nielsen’s (1992) and Bedard’s (2005, 2006, 2007, 2014) algorithms and melt compositions and temperatures described in the text. The ranges given represent the extreme liquid lines of descent as proposed for the Skaergaaard intrusion with Fe-enrichment first, followed by Si-enrichment. Underlined partition coefficients are for included elements. Orthopyroxene partitioning coefficient was not calculated for UZb,c. Single values record similarity for the two melt models. Orthoclase and zircon partitioning in UZc were included as constants based on Geochemical Reference Model (GERM; https://earthref.org/GERM/).

The transition metals (Sc, V, Cr, Co, Ni, and Zn) are partitioned principally into magnetite and ilmenite, Sc, Cr and Co also into the pyroxenes, and Co and Ni also into olivine (Table 23). The partition coefficients increase for most of the elements with height in the stratigraphy, caused by decreasing temperature, melt evolution and mineral variables as also demonstrated by Nielsen et al. (1992, 1994) and Nielsen & Beard (2000). On the other hand, the differences in the calculated partition coefficients for Cr, Ni, Sc and V (Table 23) for the two liquid descent models can only be caused by differences in the melt compositions, since both temperature and mineral compositions are identical for the two models.

In contrast to the other transition metals, Ni is principally incorporated into olivine (D_Ni = 35 at the MZ level), to a lesser extent into clinopyroxene (D_Ni = 17), and orthopyroxene (D_Ni = 8; Table 23). It is well established that D_Ni for olivine is dependent on melt composition to the extent that a marked increase with decreasing forsterite content, decreasing temperature and melt fraction of SiO₂ is plausible (Hart & Davis 1978; Kinzler et al. 1990; Bédard 2005; Li et al. 2003; Li & Ripley 2010). Thus, the increase and divergence in D_Ni for olivine in the UZ can be attributed to variation and differences in melt SiO₂, again considering that temperature and olivine compositions are identical for the two liquid line of descent models.

The alkali elements Rb and Ba are principally partitioned into the melt with only small amounts going into plagioclase, resulting in D_Rb= 0.11 and D_Ba= 0.14 at the MZ level. For plagioclase, D_Rb increases and diverges markedly through UZ, as do the D values for many of the transition elements. Experimentally determined D_Rb and D_Ba values increase as a function of decreasing An of plagioclase and MgO and SiO₂ melt contents (Bédard 2006), supporting the general findings of Nielsen (1992). On the other hand, Sr is predicted to be partitioned principally at the level of MZ, if present, into apatite (D_Sr= 1.5) and to a lesser extend into plagioclase (D_Sr= 0.76) and clinopyroxene (D_Sr= 0.60). The calculated irregular variation of D_Sr for plagioclase as a function of stratigraphic height contrasts to the summary of Bédard (2006) who predicted an increase in D_Sr with decreasing An content of plagioclase and increasing SiO₂ of melt. Strontium, however, is known to be included in apatite (Prowatke & Klemme 2006; Watson & Green 1981) and to a lesser extend in clinopyroxene (Bédard 2014), consistent with the modelling results.

The high-field strength elements Zr and Nb partition into ilmenite (D_Zr = 7.5 and D_Nb = 19) and for Zr also to a much lesser extent into apatite (D_Zr= 0.36) and clinopyroxene (D_Zr= 0.13), all reported at the MZ level. The modelled values for ilmenite partitioning are high compared to experimental determinations of D_Zr and D_Nb by Klemme et al. (2006) and Parker et al. (2011) at, or just below, unity for synthetic Ti-rich silicate systems. The REE together with Y partition into apatite with D_Y= 9–11 and D_REE= 4–7 at the MZ level and diverge through the UZ like other trace elements related to differences in the increase in SiO₂ consistent with the observations of Watson & Green (1981) and Prowatke & Klemme (2006). REE and Y are also moderately partitioned into clinopyroxene (D_La = 0.10, D_Yb= 0.70, and D_Y = 0.70, all at the MZ level). Bédard (2014) reviewed the existing experimental information on trace element partitioning into clinopyroxene. He observed that the partitioning is dependent on temperature and melt composition and that many elements in felsic and mafic melts formed coherently, slightly increasing D-trends with decreasing temperature and other compositional variables, reflecting advanced fractionation, although the most evolved felsic melts were rarely found to be collinear with intermediate and mafic melts.

5.11.3 Bulk partition coefficients (D^*)

The calculations of the D_i^* values are summarised in Table 23 for the individual zones and subzones. Used for the calculation of D_i^* are the observed average modes (Table 2), the estimated trapped-melt content after Tegner et al. (2009), and the calculated D_i values summarised in Table 23. In addition, the partition in UZc into orthoclase for Rb, Sr and Ba was based on the Geochemical Earth Reference Model database (GERM 2016), and the partition for zircon in UZc was likewise included, based on a small amount (0.02 wt%; Wager & Brown 1967). Because of its low concentrations of trace elements, quartz was not included in the calculations. Other minor mineral phases are not considered (e.g. sulphides and alloys); this later omission means that Cu could not be modelled.

Fig. 60 shows the variation in D_i^* for selected elements (Sc, V, Rb, Ba, Yb and U) as a function of stratigraphic height. The results allow a preliminary definition of the Skaergaard trace elements into either excluded (D_i^* < 1.0) or included (D_i^* > 1.0) elements – the latter is identified by underlined values in Table 23. The majority of the transition elements are consistently included, while of the excluded elements, only Rb, Ba, and U are truly excluded (<0.15) due to the presence of apatite, suggesting that these elements are reasonable candidates for trapped-melt estimates (e.g. Tegner et al. 2009). Other minor mineral phases are not considered (e.g. sulphides and alloys); the later omission means that Cu could not be modelled.

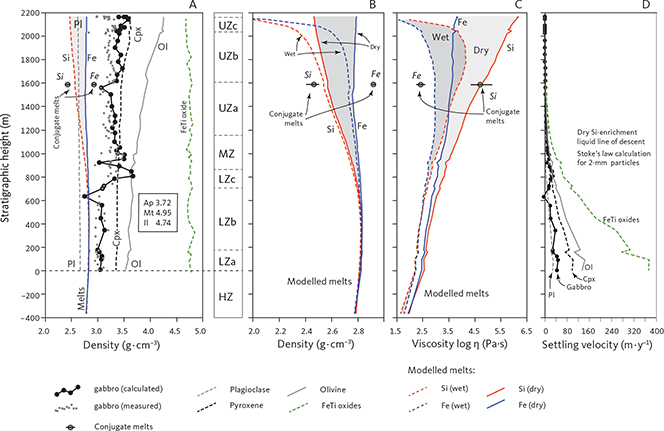
Fig. 59 Density (g·cm^–3) and viscosity (Pa·s) as a function of stratigraphic height (m) in the LS. A: Calculated density of primocrysts (Pl: plagioclase. Cpx: clinopyroxene. Ol: olivine), gabbro and FeTi oxides. Pl, Cpx and Ol are calculated using the temperature- and compositional-dependent equations of Niu & Batiza (1991a, b). Pressure effects are minor within the range assumed for the Skaergaard intrusion (60–130 MPa) and are not considered here. The density of low-Ca pyroxene has been calculated together with high-Ca pyroxene (marked as Cpx). Densities of apatite (Ap), magnetite (Mt) and ilmenite (Il) are also shown and assumed to be typical values. The densities of gabbro and FeTi oxide are based on calculated modal contents (Table 2). Measured densities of gabbro are shown for comparison and use Archimedes’ principle. The range in melt variation between the two, end member modelled compositions are marked as Si and Fe (see Supplementary Tables S1 and S2, respectively, and panel B for details). The conjugate melts (Si and Fe) are from Charlier & Grove (2012) and are given as averages, with 1σ SD. B: A focussed view of the calculated densities of the two, end-member liquid lines of descent (Si and Fe) from panel A. Grey shading shows the variation in melt for the dry liquidus. The wet liquidus is calculated for an initial H₂O content of 0.1 wt. Conjugate melts in A. C: Calculated dynamic viscosities (Pa·s) of the modelled melts. The fields for the dry and wet liquidi are shown for the two, end-member liquid lines of descent. Conjugate melts in A. D: The settling viscosity (m·y^-1) calculated from Stokes’ law for 2 mm diameter particles or clusters. Calculated from the dry Si-enrichment liquid line of descent (Table S1).

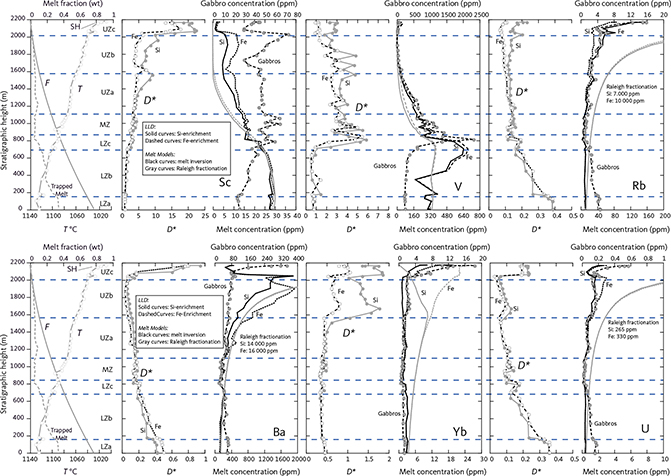
Fig. 60 Selected trace elements (Sc, V, Rb, Ba, Yb and U) from gabbros and modelled melt as a function of stratigraphic height (m) in the LS. First column shows the trapped melt and fraction of melt remaining (F) from Tegner et al. (2009) and the liquidus temperature (T) calculated from Thy et al. (2009a, 2013). For each selected trace element is shown the bulk distribution coefficients (D^*, Eq. (8)), trace element concentrations (ppm) in gabbros (data in Table 13), inverted melt composition (Eq. (9)), modelled melt composition assuming perfect Rayleigh fractionation (Eq. (11)) and initial melt compositions for the bottom of the column. The calculation of the individual melt/mineral distribution coefficients are described in Section 5.11.1. Two different solutions are shown for D^* and all melt compositions, based on the two contrasting Liquid Lines of Descent: prolonged iron enrichment past FeTi oxide appearance (Fe) and iron depletion and silica enrichment following the appearance of FeTi oxides (Si). The maximum concentrations in ppm for Rayleigh fractionation at the SH are given for truncated diagrams (Rb, Ba, U).

By definition, values of D_i^* depend on the modal content. Because the trapped melt content is included in the calculations, D_i^* will approach unity with increasing trapped-melt content at the base of the LS (Tegner et al. 2009); D_i^* increases for excluded elements and decreases for included elements due to the content of trapped melt (Table 23). The two modelled liquid lines of descent shown in Fig. 60, from F = 0.76 to F = 0, are initiated at identical values F = 1, below the base of the stratigraphic column because of the presumably similar melt compositions (H = 365 m). The D_i^* values may thus vary as a function of melt composition and stratigraphy but are constrained by the initial value F = 1. The differences seen in the D_i^*-values, if any, are mostly a function of differences in the melt compositions and modal mineralogy, not in temperature, since that is identical for the two melt models.

The calculated D_i^* values reflect the large scatter in the bulk-gabbro modal make-up, even after being reduced by the stepwise average compositions (Table 13), although the scatter is somewhat reduced compared to those observed by McBirney (1998, 2002). Common for many of the predominantly included elements is an upward transition from excluded to included status (Tables 23). For V, Sc, Co, Zn and Nb, the D_i^* values increase with modal FeTi oxide minerals in the LZc to MZ. Of these elements, only Sc shows a positive correlation with modal clinopyroxene, consistent with the high D_i value for this phase (Table 23). Surprisingly, there is no clear positive correlation between Cr content and modal pyroxene or FeTi oxide, even though this would have been expected from the D_i values. Only the Sr content shows positive correlation with modal plagioclase as reflected by D_i just below unity and likewise only Ni correlates positively with modal olivine, but not with modal pyroxene as again expected from the D_i values.

Of the excluded elements, only Rb, Ba and U are consistently excluded throughout the LS, and their D^* values are consequently strongly affected by the trapped-melt component in the LZa and LZb (Fig. 60; Table 23). REE and Y are excluded elements in the lower part of the intrusion, but transition towards an included status in the UZb with the appearance of apatite.

The effect of the melt composition on D_i^* is first manifested in the MZ where the two liquid lines of descent models start to diverge, resulting in differences in the UZ by a magnitude of approximately two. This is mainly attributed to the differences in the terminal Si content (56% versus 74% SiO₂) resulting in increased D_i^* values for the latter liquid line of descent.

One significant limitation to this modelling is the assumption we made at the outset that F = 0 at the top of UZc. While this constraint was imposed by Tegner & Cawthorn (2010) in computing their liquid lines of descent, it may not strictly be the case. For example, the forward models of Andersen (2006), Nielsen et al. (2009) and Hunter & Sparks (1987), respectively, assumed 2%, 5% and 18–25% liquid remaining after crystallisation of UZc. The D_i^* values may thus vary as a function of stratigraphy, but the differences are mostly functions of melt compositions and modal mineralogy, and only slightly due to temperature.

5.11.4 Trapped melt content

The F_TM was modelled by Tegner et al. (2009) using excluded elements (P, Rb and U) and D_i values iteratively adjusted for a trapped-melt content assuming that D_i^* are equal to the trapped-melt fraction (cf. Fig. 60, Rb). The results showed a marked decrease in F_TM from a high value (c. 45%) at the base of LZa to c. 3% at the top of LZc (Fig. 61; Table 24). Above the LZ, trapped melt was shown to steadily approach a few percent in UZb. The UZc was not included in the study by Tegner et al. (2009).

Table 24 Summary of preferred modes used for the trace element modelling including trapped melt

Zone	Stratigraphic height (m)		Melt	Ol	Opx	Cpx	Pl	Mt	Il	Ap	Kfs	Q
	high	low	(wt%)	(wt%)	(wt%)	(wt%)	(wt%)	(wt%)	(wt%)	(wt%)	(wt%)	(wt%)
A: Calculated assuming perfect fractional crystallisation
UZc	2165	2164	0.15	17.14		22.93	40.73		3.69	1.36	9.09	4.89
UZc	2165	2165	0.14	19.56		27.81	37.72		3.53	0.87	7.05	3.29
UZc	2163	2147	0.17	21.09		32.63	28.87		5.09	1.60	7.08	3.46
UZc	2144	2141	0.43	19.58		32.80	31.41		4.75	1.46	6.81	2.76
UZc	2091	2081	0.50	22.58		36.44	26.13		4.81	1.79	5.47	2.26
UZc	2075	2060	0.67	15.76		42.34	33.17		5.10	1.79	0.83	0.33
UZc	2060	2046	0.84	20.53		39.73	30.18		5.29	1.85	0.99	0.56
UZb	2044	2030	1.24	20.84		34.35	37.21		4.44	1.22	0.43	0.26
UZb	2024	1984	1.09	19.75		24.11	38.54		3.60	1.09	11.23	0.60
UZb	1962	1921	1.53	21.99		29.87	39.45	0.43	4.76	1.97
UZb	1902	1862	2.13	23.50		23.90	42.06	0.16	5.38	2.87
UZb	1843	1801	1.97	22.23		18.80	46.74	0.95	5.88	3.43
UZb	1782	1748	2.54	23.53		19.45	39.83	3.92	6.56	4.17
UZb	1728	1691	1.89	25.71		19.13	40.26	0.65	7.62	4.74
UZb	1671	1630	2.34	26.70		13.04	37.76	3.58	9.15	7.43
UZb	1620	1600	2.42	20.18		21.31	39.56	2.89	7.09	6.54
UZa	1561	1527	2.68	10.56		32.68	38.97	5.39	6.75	2.96
UZa	1506	1431	4.39	7.73	4.73	25.76	46.65	3.03	7.58	0.13
UZa	1403	1343	2.85	8.85	0.81	31.12	44.64	2.49	9.17	0.06
UZa	1323	1282	2.78	6.53	3.62	30.06	44.92	3.69	8.23	0.16
UZa	1268	1237	2.89	11.48	0.00	31.65	40.59	4.98	7.92	0.48
UZa	1218	1188	4.91	7.06	0.06	34.96	39.44	6.51	6.93	0.13
UZa	1178	1131	4.32	3.79	1.24	37.95	40.21	3.06	9.24	0.19
MZ	1098	1055	3.75	1.51	3.83	36.17	39.67	6.36	8.57	0.13
MZ	1053	1032	2.23	0.22	8.12	24.82	45.78	4.39	14.33	0.10
MZ	1024	1009	3.37	0.00	8.49	37.80	31.46	0.86	18.02	0.00
MZ	1003	1002	3.03	3.37	7.80	34.49	36.12	5.37	9.76	0.06
MZ	988	961	2.95	0.84	4.80	29.71	41.47	7.88	12.28	0.06
MZ	953	930	3.33	4.03	3.80	41.19	26.18	3.87	17.51	0.10
MZ	921	900	2.40	1.98	2.82	31.21	36.15	10.54	14.85	0.06
MZ	890	875	2.62	1.69	5.97	27.79	47.99	4.37	9.50	0.07
LZc	847	816	2.83	3.75	0.03	29.73	41.39	6.88	15.33	0.06
LZc	808	798	2.41	6.00	2.90	27.18	29.45	10.11	21.44	0.51
LZc	784	742	4.78	5.19	2.61	22.61	30.23	6.55	27.84	0.21
LZc	723	703	8.02	1.91	6.84	39.66	31.45	4.13	7.90	0.09
LZb	703	681	6.23	6.20	8.19	32.12	43.60	1.67	1.88	0.12
LZb	634	580	9.99	4.38	10.75	24.71	45.85	1.36	2.34	0.63
LZb	558	488	10.74	3.11	7.87	29.77	46.22	0.35	1.57	0.36
LZb	447	367	13.37	7.90	10.16	23.98	42.54	0.22	1.69	0.14
LZb	346	221	12.99	5.69	13.11	20.34	45.71	0.40	1.65	0.11
LZb	177	173	21.28	2.17	11.59	19.81	39.67	3.58	1.82	0.09
LZa	161	137	24.56	2.72	12.61	12.68	45.26	0.29	1.74	0.15
LZa	125	107	27.73	5.74	11.99	10.53	41.46	0.87	1.46	0.22
LZa	96	27	25.92	8.03	16.77	8.03	38.07	1.03	1.90	0.25
LZa	7		31.06	9.34	11.71	9.42	36.33	0.46	1.47	0.21
B: UZc including adjusted granophyre content calculated from quartz, orthoclase, and part of plagioclase
UZc	2165	2164	21.16	19.56		27.82	27.06		3.53	0.87
UZc	2165	2165	21.55	21.10		32.65	18.02		5.09	1.60
UZc	2163	2147	19.62	19.64		32.90	21.61		4.76	1.46
UZc	2144	2141	16.29	22.60		36.48	18.02		4.81	1.79
UZc	2091	2081	3.18	15.78		42.40	31.75		5.11	1.79
UZc	2075	2060	4.25	20.56		39.78	28.25		5.30	1.85
UZc	2060	2046	2.80	20.91		34.46	36.15		4.46	1.22
Compare to Table 2 showing the mineral modal variation without trapped melt. Stratigraphic height is given as high and low referring to the interval used for averaging. Ol: olivine. Opx: orthopyroxene. Cpx: clinopyroxene. Pl: plagioclase. Mt: magnitite. Ap: apetite. Q: quartz. Kfs: Orthoclase.

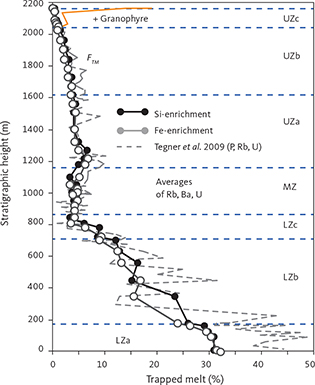
Fig. 61 Modelled trapped melt (%) as a function of stratigraphic height (m) in the LS. Model uses D^* for selected excluded elements (average of Rb, Ba, U) and Eq. (12), (Table 24). Two models are shown for Si-enriched and Fe-enriched melt, respectively. The results of the present study based on P, Rb and U are compared to that of Tegner et al. (2009). The effect of allocating the granophyre component in the UZc to the trapped melt is shown by a solid orange curve (labelled + Granophyre; data from Table 24). Blue horizontal dashed lines: divisions of the LS. Abbreviations for LS divisions in Fig. 2. F_TM: fraction of trapped melt.

The calculated D_i^* coefficients in this study allow a re-evaluation of F_TM including elements that are not highly excluded from the crystallising assemblage (Fig. 61). The resulting variation in F_TM with the stratigraphic height as averages for Rb, Ba and U resembles that of Tegner et al. (2009) with an initial total amount of 32% for the LZa, a systematic decrease upwards to 9% at the base of LZc, followed by a slight increase to 4% into the base of the MZ. This is followed by a systematic decrease to 2–3% at the top of UZb, followed by a systematic increase in the SH (Table 24A).

In contrast to the low modelled F_TM in the UZc, high residual melt components are suggested by the granophyre component widely interpreted as end-stage differentiation products for which crystallisation approaches ‘eutectic’ control (Wager & Brown 1967, p. 240). The modal estimates (Fig. 15; Table 2) point towards an increasing amount of modal quartz and orthoclase in UZc, reaching a total modal sum of 14% for quartz and orthoclase in the SH (Table 2) that resides in a granophyre component of the gabbros (Figs 13, 14). The modal composition of the granophyre patches and veins is mainly quartz, orthoclase and albite (Wager & Brown 1967; Naslund 1989; Hirschmann 1992). Although quartz and orthoclase can be equated with the values in Table 2, an amount of albite is included in the calculated plagioclase mode. Wager & Brown (1967, p. 138) estimated 10% of albite phenocrysts in a granophyre vein associated with the Tinden sill. A better modal estimate of groundmass granophyre, based on normative composition, is perhaps provided by Barker (1970) as 37% quartz, 29% orthoclase and 34% albite, approximating the granitic minimum (Tuttle & Bowen 1958). Using this modal composition for the interstitial Skaergaard granophyre and accepting the interpretation that the UZc granophyre represents an interstitial melt, it is possible to recast the modes for the samples collected as part of this study to include a realistic granophyre component reaching an average of 20% in the upper part of UZc (Fig. 61; Table 24B).

The critical issue, however, is whether the granophyre component of the SH ferrodiorites can be taken as the end-stage melt for terminal fractional crystallisation approaching ‘eutectic’ control, as suggested by Wager & Brown (1967) and widely assumed to be the case. Next, we consider the extent to which crystal fractionation processes can quantitatively account for the geochemical systematics observed in the LS and the possible effects of liquid immiscibility in the UZ.

5.11.5 Perfect fractional crystallisation

The evolution of the trace elements is shown for selected included and excluded elements in Fig. 60 for the two liquid descent models. The melt compositions were calculated in two different ways. Firstly, the melt concentration was inverted from the gabbro composition using the bulk partition coefficient and Eq. (9). Secondly, the trace element concentrations were modelled assuming perfect Rayleigh fractionation using Eq. (11) and making some reasonable assumptions for the initial melt compositions at F = 1 or at c. 365 m depth in the HZ. The similarities or differences between the two sets of calculated melt compositions can be used to evaluate whether perfect fractional crystallisation was a major operator during solidification.

The variation seen in the inverted melt composition for included elements conforms reasonably well to the prediction from perfect fractional crystallisation (like Sc and V in Fig. 60). The LZ often displays marked fluctuations around the predicted trend for perfect fractional crystallisation that can be attributed to uncertainties resulting from sampling the strongly heterogeneous layered gabbros (e.g. V). With advanced fractionation, the variation in inverted melt converges to the strongly depleted trend of fractional crystallisation that characterises ideal included elements reaching low levels of depletion late in the stratigraphic sequence (Ni, Cr and V).

Few of the excluded elements are truly excluded throughout the complete stratigraphic sequence. The elements shown in Fig. 60 (Rb, Ba and U) are initially excluded, although with bulk partition coefficients often elevated by the inclusion of trapped melts. With advanced stages of fractionation, and the appearance of FeTi oxides, the bulk partition coefficients often exceed unity (Zr and Nb), particularly for the Fe-enriched model for the liquid line of descent. The excluded elements, nevertheless, immediately show strong deviation from the perfect Rayleigh fractionation curve, failing to reach sufficiently high melt concentrations. The only exception is Ba, which shows reasonable correspondence between the inverted and fractional crystallisation melt compositions still into the UZb (Fig. 60).

The fractionation trends for three selected trace elements (Rb, Sc and Yb) are illustrated in Fig. 62 and compared to perfect fractional crystallisation for bulk distribution coefficients (D_i^*). As previously noted, the included elements, like Sc, reasonably conform to the Rayleigh fractionation trend for variable values of D_i^* (i.e. >1). This suggests only a modest underestimation in the D_i^* values of Fig 62 (1.2–2.0). On the other hand, the excluded elements, like Rb and Yb, strongly deviate from the Rayleigh fractionation trends despite the predicted D_i^* values for Rb of about 0.1 and Yb of about 0.4; for the latter, the saturation of apatite is followed by an increase to about 1.0 in UZc. Although these D_i^* values appear reasonable, the estimated melt compositions that use them are largely constant throughout the stratigraphic sequence, suggesting included D_i^* values of 0.8–1.0.

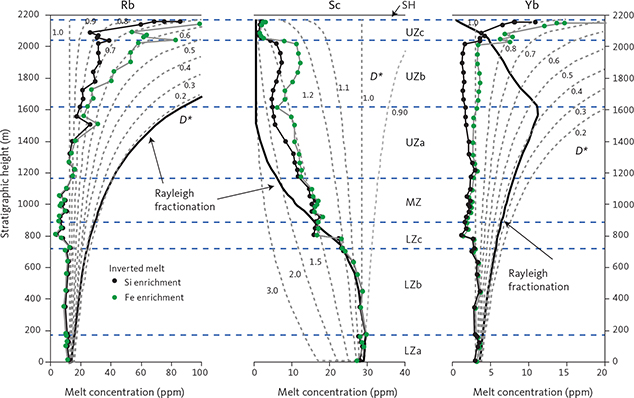
Fig. 62 Inverted melt concentrations of Rb, Sc and Yb (ppm) compared to variable Rayleigh fractions using the modelled D^*values and ranges of constant D^* values. Si enrichment and Fe enrichment refer to the two contrasting liquid lines of descent: Fe: prolonged iron enrichment past FeTi oxide appearance, and Si: iron depletion and silica enrichment following the appearance of FeTi oxides. Blue horizontal dashed lines: divisions of the LS. Abbreviations for LS divisions in Fig. 2. Solid black curve: perfect crystallisation (D^* = 0). Grey dashed curves: Constant D^* values (0.2 to 1).

None of the examined elements correspond to the inverted and the predicted fractional crystallisation melts. However, the overall impression is that the included elements conform more closely to a first order fractional crystallisation model than the excluded elements. This supports a strong decoupling between the excluded and the included (major and trace) elements. These observations show that a unifying crystallisation process cannot explain the two groups of trace elements and that losses of significant amounts of excluded elements from the crystal mush prior to final solidification of the gabbros must be involved.

5.11.6 Imperfect fractional crystallisation

The melt composition evolves for perfect fractional crystallisation by removing or isolating early-formed crystals and thereby changing the melt composition in the crystallisation zone and eventually the bulk magma chamber, only if the residual melt is recycled into the main chamber. Perfect fractional crystallisation is nevertheless unlikely in a cooling magma chamber like the Skaergaard intrusion, where components of equilibrium or imperfect fractionation may have been involved. The evolution of trace elements during ideal equilibrium crystallisation can be approximated using fractional crystallisation, Eq. (10), assuming constant concentrations for each segment throughout the column fixed by its initial value F = 1. Consequently, the initial melt composition will be approximately identical to the final composition because no solid material is removed from the crystallising system.

Calculations of imperfect fractional crystallisation are illustrated in Fig. 63 for a variable component of equilibrium crystallisation and for three selected elements: Rb and Yb represent the excluded elements with low bulk partition coefficients, and Sc represents the included elements with moderate coefficients. For the excluded elements, the inverted melt compositions correspond reasonably to the predicted ideal equilibrium crystallisation (Rb and Yb). For some excluded elements, like Yb, the inverted compositions predict an apparent equilibrium component > 100%, likely to be attributed to small errors in D^*. In contrast, the included elements, like Sc, suggest a dominant mode of fractional crystallisation with only a modest equilibrium component at c. 40% in the MZ, UZa and into UZb. The poor correspondence, as observed for perfect fractional crystallisation, between the included and excluded elements again points towards the loss of a component of excluded elements, as observed in modelling of perfect fractional crystallisation. The modelling for Sc, however, suggests equilibrium components of 40% in the MZ and UZa and high values at the top of UZb. Furthermore, the excluded elements Rb and Yb imply near complete equilibrium that could have controlled crystallisation (Fig. 63). This contrasts with the observation that all silicate minerals show strong and systematic variation in the overall stratigraphic column, proposing a dominant fractional crystallisation (Figs 25–28).

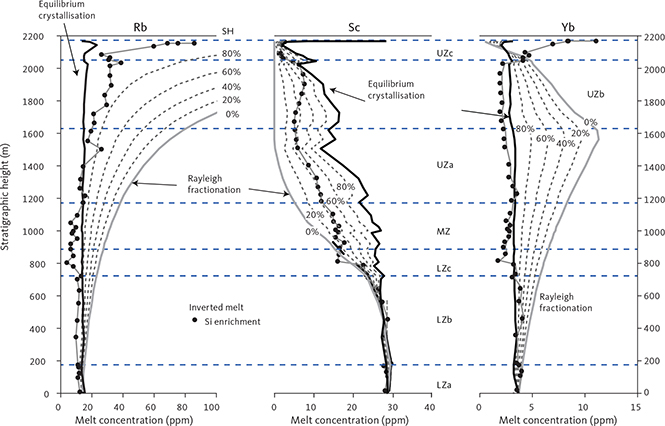
Fig. 63 Modelled melt concentrations (ppm) of Rb, Sc and Yb for imperfect fractional crystallisation as a function of stratigraphic height (m) in LS. Perfect fractional crystallisation is shown for comparison. Curves are shown for 100, 80, 60, 40, 20 and 0% equilibrium crystallisation calculated for the Si-enrichment liquid line of descent. Blue horizontal dashed lines: divisions of the LS. Abbreviations for LS divisions in Fig. 2. Solid black curves: perfect equilibrium crystallisation (100%). Solid grey curves: perfect reaction crystallisation (0%). Dashed curves: imperfect crystallisation (80–20%).

5.11.7 In situ boundary-layer crystallisation

Modelling of fractional crystallisation implicitly assumes that primocrysts form homogeneously in the melt, controlled by phase equilibria and cooling, and are immediately removed and isolated in a bottom mush layer by various gravitative or convective processes. The magma that occupies pore spaces in the mush is thought to return to the convecting magma principally by compaction. Studies have nevertheless emphasised that heat loss and crystallisation of a cooling magma chamber may occur heterogeneously at the margins in narrow transition zones between the liquid and solid strata (e.g. Jackson 1961; Morse 1986; Marsh 1988; Tait 1988; Jaupart & Tait 1995; Nielsen 2016). Trace element concentrations of in situ boundary-layer crystallisation have been modelled by Langmuir (1989) and Nielsen & DeLong (1992). The principal difference between boundary-layer and homogeneous-chamber crystallisation is that for the former the melt in the pore spaces is returned to the main magma body, principally by compositional density convection, while in the latter, melt is compacted out of the mush. These differences in mush formation may not be distinguished petrographically, but the difference in the overall liquid line of descent may offer some clues (Langmuir 1989).

Boundary-layer crystallisation implies that sub-liquidus stable phases may affect the overall fractionation as opposed to what would be expected from equilibrium liquidus relations. Also, excluded element concentrations and ratios will be enriched more than included elements for in situ crystallisation compared to fractional crystallisation, and thus enhance the decoupling between excluded and included elements. The formulation for in situ crystallisation, Eq. (13), proposed by Langmuir (1989) is used in Fig. 64 to illustrate the predicted variations for selected trace elements (Rb, Sc, and Yb). Curves for solid fractions (S) of 0.00, 0.25, 0.50, 0.75 and 1.00 are shown. The solid fraction of 0.50 is assumed to be a reasonable average for the Skaergaard in situ crystallisation zone, as suggested by Langmuir (1989) for the Kiglapait intrusion. The F_TM is calculated as shown in Table 24, and the remaining melt is returned to the main chamber (for S = 0.50, the returned amount varies as a function of F_TM between c. 0.25 and 0.50).The inverted melt composition for the two excluded elements Rb and Yb correspond to curves for constant and very low return of melt to the main magma (S << 0.25), while the moderately included Sc corresponds to curves for high return in the lower and middle parts of the column (S = 0.75–1.00) to a decreasing return throughout most of the UZ (S = c. 0.50). These diverse predictions for the fraction of melt returned for excluded and included elements confirm their strong decoupling as encountered for other crystallisation models and are not easily explained by crystallisation models (fractional or in situ).

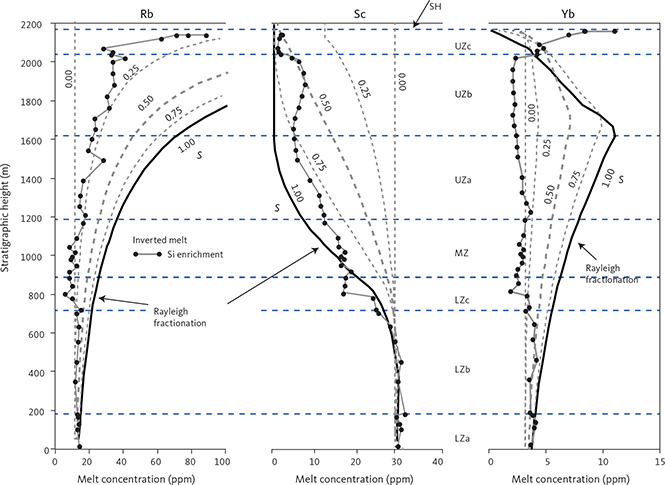
Fig. 64 Modelled melt concentrations (ppm) for in situ crystallisation of Rb, Sc, and Yb as a function of stratigraphic height (m) in the LS. Perfect fractional crystallisation and inverted melt compositions shown for comparison. Trapped melt content and D^* are based on the modes in Table 24. Grey dashed curves: solid fractions in the crystallisation front (S) of 0.25, 0.50 and 0.75, where sum of the solid fraction plus trapped melt and returned melt to the main magma is equal to 1. Black solid curve for S = 1.0is equivalent to perfect fractional crystallisation, while the grey dashed line for S = 0.0 displays constant variation equivalent to the initial concentration (C_o, see Langmuir (1989)). Blue horizontal dashed lines: divisions of the LS. Abbreviations for LS divisions in Fig. 2.

A low return fraction of melt (<0.25) to the main chamber will reduce or for an extreme condition (S = 0.00) prohibit in situ fractionation, while a high return fraction of melt will promote in situ fractionation effects. In the extreme, in situ fractionation for a complete melt return (S = 1.00) will be equal to perfect Rayleigh fractionation (Fig. 64). Because of the low trapped-melt content modelled for the main part of the Skaergaard LS, in situ crystallisation does not offer a solution to the observed variations in trace element. See Sections 5.12 and 5.13 for a discussion of models for trapped melts accounting for effects of liquid immiscibility.

5.12 Role of liquid immiscibility

5.12.1 Evidence for liquid immiscibility

The idea that liquid immiscibility affected the late-stage liquid evolution of the Skaergaard intrusion is not new. It was first proposed by McBirney & Nakamura (1974) and McBirney (1975) based on melting experiments using mixtures of granophyre and UZb and UZc ferrodiorites. This proposal was strengthened by the analysis and recognition of melts as inclusions in apatite, olivine and plagioclase (Jakobsen et al. 2005, 2011), pointing towards an emulsion of Si-rich melt and Fe-rich droplets in the mushes and in the late stages of the magma chamber. Experimental atmospheric support was provided by Charlier & Grove (2012) and Honour et al. (2019a) on samples resembling potential Skaergaard melts. Further support was offered by Veksler et al. (2007, 2008) by centrifuge experiments showing liquid immiscibility in Skaergaard-like MZ melts (see also Veksler 2009; Veksler et al. 2009).

Petrographic studies of interstitial material in the lower part of the intrusion have also invoked the actions of immiscibility melts to explain textural and chemical observations (Humphreys 2009, 2011; Holness et al. 2011). Further, Nielsen et al. (2015) have proposed a mechanism for the formation of the Skaergaard PGE-Au Mineralisation that incorporates migration of both iron-rich and silica-rich immiscible melts in the upper part of the intrusion. There is thus little doubt that the formation of conjugate immiscible melts can and indeed did affect the Skaergaard liquid line of descent and thus deserve careful consideration.

Following Jakobsen et al.’s (2005, 2011) discovery of trapped emulsion droplets of melt in the UZ gabbros, it was also expected that macroscopic and geochemical evidence for the action of liquid immiscibility during the solidification of the Skaergaard intrusion would be found as part of this study. Thus, the appearance of a high olivine and apatite base to the UZb and a high granophyre concentration at the top of UZc are seen as evidence for the action of immiscibility and the formation of an apparent zoned upper part of the UZ (Figs 15, 52C; see also Sections 4.2 and 5.7).

Additional evidence for immiscibility is seen in the decoupling of included and excluded trace elements throughout the LS that we relate to the migration of late-stage granophyre in the gabbro mush (see Section 5.11). These observations suggest that liquid immiscibility may have affected the evolution during crystallisation of both the residual magma chamber and solidification of the melt trapped in the mush across the entire intrusion. This interpretation appears to contrast with the suggestion by Nielsen et al. (2015) that immiscibility occurred in the mush and only indirectly affected the main chamber by buoyancy-controlled upward migrating granophyre. In this section, we develop a simplified intrusion-wide model for the effect of immiscibility on the liquid line of descent of trace elements that can explain the decoupling of included and excluded elements. We base this on the observations as well as reasonable assumptions of the behaviour of the trapped melt in the mush as well as the residual magma chamber.

5.12.2 Liquid immiscibility and crystallisation in the residual chamber

A summary of the model used here is shown in Fig. 65 as simplified and schematic interpretations of the evolution of the Skaergaard terminal magma chamber. It is suggested that magma convection in the residual chamber (Fig. 65A) is terminated by liquid immiscibility (Fig. 65B) and that partial buoyancy separation of the two cognate melts effectively results in a zoned chamber (Fig. 65C) that with cooling crystallises as a mixture of ferrodiorites and granophyres (Fig. 65D).

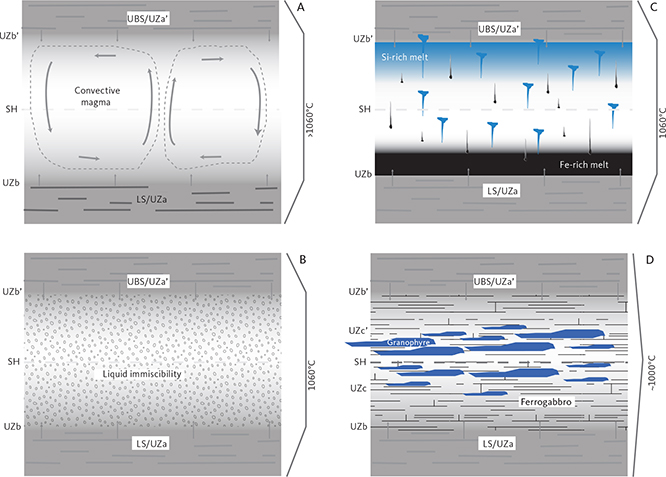
Fig. 65 Schematic illustration of the proposed late history of the terminal Skaergaard magma chamber (UZb and UZc). A: UZa convecting chamber at just above 1060°C and a melt fraction of 0.10, sandwiched between the upward-moving UZa of the LS and the downward-moving UZa’ of the UBS. B: Onset of liquid immiscibility when the temperature reaches 1060°C by the formation of basaltic iron-rich droplets in a homogeneous silicic melt, effectively terminating chamber convection. C: Separation of the two cognate melts with the Si-rich melt preferentially migrating upward and the Fe-rich melt droplets migrating downward (or remaining stationery). This results in an effectively zoned residual chamber with the Fe-rich melt component concentrated principally at the base and the Si-rich melt concentrated at the top under the UZa’. Immiscibility is subsequently terminated by the melt separation and the drop in temperature to unknown values. D: Final crystallisation products at solidus temperatures (c. 1000°C and F = 0) are made up of a ferrodiorite (andesine, olivine and pyroxene) with granophyre (albite, orthoclase, and quartz) dispersed dominantly in the UZc and UZc’ from a microscopic interstitial to macroscopic lenses and sill scales. The granophyre component dominates the UBS. Part of the UBS is thought to have been intruded into the surrounding host rocks. Illustrations are not to scale.

The onset of immiscibility in the main residual chamber of the Skaergaard intrusion is observed to have occurred at the UZa–UZb boundary (Fig. 50) at a temperature of c. 1060°C for a magma saturated in plagioclase (An₄₀), olivine (Fo₃₉), clinopyroxene (Mg# 50) and FeTi oxides (see Section 5.7.7). We estimate that the SiO₂ and FeO* contents at the onset of liquid immiscibility were 65% and 14% for the Si-enrichment trend, while they were 54% and 26% for the Fe-enrichment trend (Tables 21, 22). We further suggest that convection in the main magma body may have ceased when large-scale liquid immiscibility developed, and the conjugate liquids separated gravitationally. The upward migration and coalescence of a granophyric component resulted in the host melt made of an apparent zoned coarse-textured mixtures of ferrobasaltic (or dioritic) and silicic melts of which the latter eventually may have formed larger bodies as dykes or sills, transitioning into the lower part of the UBS or the host rocks (e.g. Jakobsen et al. 2011; Salmonsen & Tegner 2013). The residual chamber would at that stage have been relatively small with an effective zoning impeding convective overturn. This would also have restricted or terminated large-scale fractional crystallisation and have resulted in an overall imperfect mode of fractional crystallisation mostly controlled by equilibrium crystallisation (see Section 5.11).

The two conjugate melts, during active immiscibility, would have been stable at an identical temperature (initially at c. 1060°C) and saturated in identical mineral compositions. Following termination of immiscibility, because of cooling and migration of granophyre, the upward growth of the crystallisation front would continue, but now in more mafic melts, resulting in the formation of the olivine-rich and apatite-rich base of the UZb (Fig. 15) and the trapping upward of increasing higher amounts of granophyre in a ferrobasalt (or dioritic) matrix (cf. Fig. 14). The two components, although having cooled down simultaneously, would, however, have behaved differently due to markedly different liquidus and solidus temperatures and phase equilibria. Compositional variations throughout UZb and UZc would then have been a result of the relative proportions, crystallisation, and reactions between the various melt components and not a consequence of protracted crystal fractionation. The details of these processes are based on our current knowledge and understanding of the effects of liquid immiscibility on the Skaergaard magma but are not predictable and will require future experimental and detailed petrographic studies.

5.12.3 Crystallisation and immiscibility in the trapped melt

The foundation for our model calculations is that the interstitial trapped melts crystallise in a similar fashion as seen for the overall intrusion. This is a simplified view of the mush pile because it considers crystallisation in the mush to occur by fractional crystallisation in a closed system without, or with limited, melt migration laterally or horizontally in the mush. However, this simplification allows estimates of the initial liquidus temperature based on plagioclase composition (Thy et al. 2013), the onset of immiscibility assumed to be at 1060°C, and the amount of liquid remaining in the mush melt zone of about 0.10 of the initial trapped melt (Tegner et al. 2009). It is possible that the trapped melt solidified with a significant component of equilibrium (imperfect fractional crystallisation), reactions with the host gabbro, or local redox conditions that allowed the trapped melt to either delay or accelerate the point of immiscibility compared to the overall differentiation processes inferred from the main chamber. Thus, detailed petrographic studies of mush gabbros (Humphreys 2009, 2011; Holness et al. 2011; Nielsen et al. 2015) have suggested that the trapped melt may have reached immiscibility prior to the similar event in the main magma chamber without, or with limited, exchange of granophyre from the mush to the main chamber. This is, however, not suggested by this study that observes macroscopic evidence for migration of both the basic and silicic cognate melt components in the UZ chamber at temperatures similar to those likely experienced by the mush (see Section 5.7.7). The modelling of the mush and chamber melt based on identical crystallisation conditions are nevertheless a simplification adopted to predict onset of immiscibility and its effects on the liquid evolution.

If the trapped melt crystallised due to perfect fractional crystallisation without reaching immiscibility to a final melt also of a granophyric or granitic composition, the liquidus temperature would have been c. 950°C or below. The amount of this residual melt would have been restricted, and it would have been difficult for the melt to buoyantly segregate from the solidification zone. Encountering the two-liquid field earlier during crystallisation of the mush liquid would have provided greater opportunity for buoyant segregation of the conjugate felsic liquid from the solidification zone at the floor of the intrusion. The porosity and permeability at the point of immiscibility is dependent on the fraction of trapped melt or the mush porosity and the physical properties of the melts. The high fractions of trapped melt mush in LZa and LZb, reaching 1060°C, would constrain the porosity to a fraction of 0.01–0.04, which may have allowed interconnected permeable flow (Turcotte 1982; McKenzie 1984, 1989). However, the greatly reduced melt fractions in the mush of LZc to UZa (Fig. 61), as well as locally, may still have acted as a barrier to granophyre migration, thus effectively trapping it in situ or only allowing lateral migration and coalescence into lenses, perhaps tectonically induced in the mush packet.

The solidification of the LZ mush mostly occurred prior to the onset of liquid immiscibility in the residual interstitial melt (Tegner et al. 2009), allowing for a crystallisation interval from c. 70°C at the base of the exposed LZa and linearly decreasing upward to the top of UZa, where a liquidus temperature of 1060°C (F ≈ 0.10) is reached in the main chamber, and immiscibility is inferred to be initiated. In the LZ and MZ residual mush, immiscibility is therefore reached well after the main crystalline framework of silicate and oxide minerals has been established and the immiscible products thus completely or partially trapped. Late-stage migration of granophyric melts may therefore mainly be controlled by ductile shear stress and shrinking fractures in the solid mush and to a lesser extent by compaction (Larsen & Brooks 1994; Jakobsen et al. 2011; Salmonsen & Tegner 2013). This results in pods and veins of granophyre and melanogranophyre in the gabbros. Approaching the UZa–UZb boundary, where the solidification interval would trend towards zero thus allowing for more interactions between crystallisation and immiscibility and thus for a higher proportion of upward migration of granophyre melt (modelled from 0% in LZa to 99% at the UZa-UZb boundary). Continued growth of the crystallisation front, following initiation of unmixing, upward and inward, is thus likely to trap conjugate melts or emulsion in larger amounts than lower in the stratigraphy (Jakobsen et al. 2011).

The silicic granophyric melt is less dense than the basic conjugate melt and the crystal network (Fig. 59; Hunter & Sparks 1987; Tegner et al. 2009). It is consequently probable that the silicic immiscible melt is able to partially migrate upward (Nielsen et al. 2015) and that its success in reaching the main magma chamber will increase from minor to unlikely in the LZ to probably successful in the UZa. The accumulative fraction of the silicic conjugate melt, assumed to be drained from below into the UZb magma reservoir, was always small because of the low content of trapped liquid and the likely interruption of migration paths. Small fractions of granophyre will have detectable effects on the UZ evolution only for elements such as Rb that are strongly partitioned into the silicic immiscible melt but local effects may still be detectable on the interstitial mineralogy and mineral compositions, as demonstrated by Holness et al. (2011) and Humphreys (2009, 2011).

The role of the primitive to evolved basaltic melt filling interstitial spaces in the mush is an unknown factor and unaccounted for in the present modelling. The physical properties and the mush porosity will control such melt migration prior to immiscibility. Because of the solidification temperature interval and upward decrease in residual melt volume, the effects of basaltic melt migration will be most pronounced in the lower part of the stratigraphy. The density of the interstitial basaltic melt is slightly lower than the coexisting primocryst plagioclase until the base of the UZa where the buoyancy reverses (Fig. 59). The melt density is also much lower than the bulk-mineral network throughout the stratigraphy. Thus, the basaltic melt could be prone to migrate upwards and laterally under appropriate porosity conditions and particularly if compaction or lateral shear stress were operative (Tegner et al. 2009). Gabbroic segregation lenses, formerly referred to as “wavy pyroxene rocks” by Wager & Deer (1939), occur in the MBS where they have been attributed to tearing and sagging in the vertical crustal mush (Humphreys & Holness 2010). Larsen & Brooks (1994) did an extensive examination of gabbroic pegmatites with geometrical shapes from discordant pods and domes in the LZ and MZ, transitioning into concordant lenses in the UZ. They attributed these to segregated and buoyantly-migrated basaltic melt that crystallised under final hydrous conditions to mimic the overall fractionation in the intrusion, including a terminal immiscible granophyre melt. It is unfortunately not possible to quantify the volume of basaltic melt that may have migrated in the mush. The effect would be to reduce the absolute volume of immiscible melts and a reduction in excluded trace elements in the final gabbros. This latter effect is considered minor and would not have strongly affected the qualitative findings due to the much higher concentration of excluded elements in the immiscible granophyre melt.

5.12.4 Predicting the effects of liquid immiscibility

The observed decoupling of included and excluded elements suggested from the forward modelling of the trace elements was related to the effects of the migration of immiscible granophyre melts in the mush or an underrepresentation of granophyre in the analysed mush gabbros (see Section 5.11). The immiscibility model formulated here allows us to evaluate the effects of this migration or loss of cognate melts. For this purpose, we use the observed gabbro column as described by composition (Figs 33–35), modal and mineralogical makeup (Fig. 15), predicted partitioning coefficients and estimated trapped-melt content (Fig. 61). As noted, we assume that immiscibility reached the liquidus at 1060°C and that 10% of the initial trapped melt remained, as for the bulk chamber melt. It should, however, be considered that the model calculations only consider the end-stage evolution of the gabbro column and its cooling to the point when liquid immiscibility occurs. Thus, it does not consider the mode of formation of the final mush, either by in situ crystallisation, compaction or a combination of these two. The purpose of the model calculations is to (1) quantify the behaviour of the UZb and UZc, and (2) quantify the possible effects of the horizontal and lateral migrations of the silicic immiscible melt in the LZa–UZa gabbro column.

The trapped-melt fraction in the gabbro mush is known, or believed to be known, from the present estimates (Table 24; Fig. 61). This means that at the point miscibility reaches the liquidus, the conditions and compositions can be taken throughout the lower gabbro column to be identical to those at the UZa–UZb boundary. We can thus predict at individual levels in the LS, as well as cumulatively, the amounts by weight of granophyre liquid that potentially may have been affected by migration, the trace element content prior to immiscibility, the trace element contents of the two conjugate melts, and temperature (taken to be a constant at 1060°C). The basic assumptions are obviously that the trapped-melt content is correctly estimated and that the sampled gabbros represent the final crystalline mush (see Section 5.11.4).

The trace element concentrations at the point of immiscibility in both the mush and the melt chamber can be estimated by Rayleigh fractionation modelling (Fig. 62). Further, the trace element compositions of the two conjugate melts can be predicted based on experimental partition coefficients between the immiscible silicic and basaltic conjugate melts for which the partitions are reasonably known (Rb, Sc and Ba for which data are available; Watson 1976; Watson & Green 1981; Veksler et al. 2006; Veksler & Charlier 2015). Rubidium is dominatingly partitioned into the silicic melt (D^S/B = 5), while Ba is about evenly partitioned (D^S/B = 0.8), and Sc is moderately partitioned into the basic melt (D^S/B = 0.5), where D^S/B is partition coefficient between immiscible silicic (S) and basic (B) conjugate melts. The partition coefficients and the concentrations of the selected trace elements in the original melt and in the two conjugate melts are shown in Table 25.

Table 25 Variables used for modelling of liquid immiscibility

Elements	Rb	Ba	Sc
Partition coefficients D (silicic (S) / basaltic (B) conjugate melts)
DS/B	5.0	0.8	0.5
DB/S	0.2	1.3	2.0
Bulk partition coefficients D* (solid/liquid)
D* UZa-UZb	0.16	0.15	7.9
D* MZ-UZa	0.16	0.18	3.7
D* LZa	0.4	0.4	0.8
Element concentrations (ppm) at Uza–UZb Boundary
Rayleigh fractionation	74	798	0.07
Silicic conjugate melt	62	363	0.02
Basic conjugate melt	12	436	0.04
T (ºC)		1061.5
F		0.105

The only other information needed is the relative proportions of the two conjugate melts. Most experimental studies have argued that the proportions of the two melts might reach a weight ratio of one (Dixon & Rutherford 1979; Veksler et al. 2007, 2008; Charlier & Grove 2012; Charlier et al. 2013). Veksler et al. (2006, 2008) examined a ferrobasaltic composition, similar to the major element composition used here, to determine the trace element partitions and obtained about equal proportions of the two conjugate melts. In contrast, our results (Fig. 53) suggest a higher proportion of the silicic (c. 80–70%) compared to the basic (c. 20–30%) conjugate melt, depending on the liquid line of descent model considered. These estimates, however, are based on forward fractional crystallisation modelling in contrast to the equilibrium experimental results. A high amount of equilibrium conditions can be expected to result in a marked steepening of the liquid decent line. For this reason, we model below both the fractional crystallisation (80% silicic melt) and the equilibrium crystallisation (50% silicic melt) modes. It is further assumed, because of the lack of knowledge, that the proportions of the two immiscible melts remain constant with decreasing T < 1060°C, until the liquidus emerges from the immiscibility field at an unknown temperature.

The basic immiscible melt both at levels below and above the UZa–UZb boundary is, with minor exceptions, taken to be fully retained where it formed in the mush. It is only assumed that small amounts of basic conjugate melt in the UZb and UZc may partially sag in the main chamber and that likewise a small component of the UBS basic conjugate melt may also migrate down into the UZ chamber (Nielsen et al. 2015). Although some of these assumptions might be questioned or refined, they will serve as first-order constraints, allowing us to predict the general effect of liquid immiscibility, although not as much the absolute effects.

Fig. 66 shows three possible 1060°C chamber models considered in the modelling of the trace elements as variations in the melt fractions of the two conjugate melts (basic and silicic) with stratigraphic height. The lower part of the intrusion is not shown because of the predominantly very low conjugate melt fractions. The first two models (in Figs 66A, B) assume a significant amount of granophyre migration out of the chamber into the UBS and host lavas. Fractions of lost granophyre are taken to be 0.38 (Fig. 66A) and 0.56 (Fig. 66B); volumetrically equivalent to 8.5 km³ and 12.4 km³ on a weight basis, respectively, using Nielsen’s (2004) volume estimates. The models differ in the assumed ratio between the silicic and basic conjugate melts: the model in Fig. 66B is scaled as 80% silicic melt and 20% basic melt, where as in Fig. 66A it is 50% silicic melt and 50% basic melt. This scaling of silica to basic melt approximates to fractional crystallisation and equilibrium crystallisation, respectively (Fig. 53). The model in Fig. 66C is similar to that in Fig. 66A, except that granophyre is not migrating out of the melt chamber. Also included is a small amount of basic conjugate melt seeping down from the upper crystallisation front (i.e. the UBS) amounting to a fraction of 0.12–0.04 km³ or 2.8–0.9 km³, dependent on the ratio of the conjugate melt used in the model. A final part of the model is a small amount of granophyre seeping up from the LS into the chamber that amounts to 0.7 or 1.1 km³ and is similarly dependent on the ratio of the two conjugate melts. The result is a modestly zoned UZ chamber, being either dominantly basic (models in Fig. 66A and C) or silicic (model in Fig. 66B) mainly dependent on the behaviour of the granophyre melt component.

Fig. 66 Liquid immiscibility mass balance models for UZb and UZc. A: Loss of granophyre from the intrusion (red) assuming 50% silicic and 50% basic conjugate melts. B: Loss of granophyre from the intrusion (red) assuming 80% silicic and 20% basic conjugate melts. C: No loss of granophyre from the intrusion assuming 50% silicic and 50% basic conjugate melts. All three models involve a small migration of granophyre from the gabbro package below (grey dashed curve) and sinking of basic melt from the UBS (black dashed curve). For details of the mass balance models, see Section 5.12.4. Abbreviations are: B: residual basic conjugate melts. S: residual silicic conjugate melts. Grey arrows: component migration down. Red arrows: component migrating out of chamber. Black arrows: component migrating up from below.

Because little quantitative information is available on both the relative proportions of the two cognate melts as well as their early and late-stage behaviour in the mush and magma chamber, the purpose of the three upper-chamber models is principally to test the general effects of (1) loss of granophyre from the intrusion, and (2) the proportions of the two melts formed from immiscibility. There are nevertheless some first-order observations that can be made. To produce the observed mafic base of the UZb (Figs 51, 52C), a high proportion of the basic conjugate melt is required – approaching 50% of the original melt. This allows us to exclude the model in Fig. 66B that would produce a consistently silicic zoned terminal sequence of the Skaergaard intrusion, and instead focus on the models of Fig. 66 A and C. This in effect means that the modelling uses equilibrium crystallisation and not fractional crystallisation for the final evolution, as also predicted from the trace element variation. It is important to realise that although zoning is used to describe the final chamber of the Skaergaard, this zoning is sensu lato caused by the increasing amount of a granophyre component towards the top and not necessarily by a sensu stricto zoned melt component.

The amount of granophyre extracted in the models from the Skaergaard magma is 8–9 km³ (model in Fig. 66A), which amounts to 4–5% of the whole LS and 38% for only the combined UZb and UZc, based on the total volumes estimated by Nielsen (2004). The question is obviously if this amount is a reasonable estimate for the LS contribution of granophyre to the UBS and the nearby host volcanics. The bulk composition of the intrusion estimated by McBirney (1989a) did not incorporate granophyre or melanogranophyre. For this reason, Nielsen (2004, table 3) added 5% of melanogranophyre to McBirney’s (1989a) bulk composition for it to be normatively comparable to the tholeiitic lavas of the East Greenland plateau (see Section 5.5). This estimate implies that a volume of 15 km³ (melano-) granophyre could have potentially made up the final differentiate in the UZc, SH and the equivalent parts of the UBS. Attempts by gabbro summation to estimate the bulk (or parental) magma compositions as well as the liquid line of descent have variably added granophyre or melanogranophyre amounting to 2% in LZ–UZa, 5–8% in UZb and 15% in the UZc (including their UBS and MBS equivalents; Tegner 1997; Nielsen et al. 2009; Andersen 2006). In these calculations, melanogranophyre was mostly added instead of granophyre because these former compositions were judged more reliable. The accumulation of such additional volumes is proportionate to the lower part of the stratigraphy (5.5 km³), to the upper part of the stratigraphy (2.4 km³) and to the total intrusion (7.9 km³).

The UZc equivalent part of the UBS (UZ’) was mapped and described by Naslund (1984) who observed that the lowermost part of the UBS was enriched in several low-melting and volatile components (SiO₂, K₂O, and H₂O), and hypothesised that these enrichments could be the result of upward migration from the underlying chamber and accumulation along the downward crystallisation front. Salmonsen & Tegner (2013) detailed the same transition in their Kilen profile and estimated the thickness of the UZc’ to be 100 m or 30% of the total UZ’ (or UBZγ³ and UBZγ, respectively, using the nomenclature of Naslund 1984). Compared to the corresponding LS, the UZc’ is relatively thicker in the central profile than the stratigraphy of the UZc, occupying 110 m or about 10% of the total UZ. These observations may suggest a relatively thicker package of gabbros on the downward moving crystallisation front of the UBS and support the hypothesis that the UZc’ received late differentiation components like granophyre from the final static chamber. The final differentiation products (UZc–SH–UZc’) were estimated by Nielsen (2004) to be distributed over an area of about 30 km² in the inner parts of the intrusion or about 6 km³, evenly distributed between the two stratigraphic parts – these are somewhat high compared to the 4–5 km³ estimated by Nielsen (2004) for the UZc alone.

The petrographic and structural make-up of the final differentiate in the uppermost subzones around the SH was not well documented (Wager & Brown 1967). Felsic differentiates of granophyre or melanogranophyre appears as pods and lenses in the UZc amounting to an estimated 15% of the gabbros (McBirney 1989a). Tegner (1997) noted that melanogranophyre lenses increased upward in the UZ towards the SH, where they amounted to 15% of the total subzone. These estimates are similar to this study suggesting approximately 20% granophyre content towards the upper part of the UZc. The description of Irvine et al. (1998) closely matches our impression that the UZc “[..] is a pegmatitic cumulate with plagioclase, olivine, hedenbergite, apatite, and magnetite being recrystallised cumulus minerals, and granophyre forming a postcumulus mesostasis.” In the UZ’ of the UBS, the amount of granophyre is believed to be higher. Although quantitative estimates of their spatial distribution are not available, an estimate of 25% appears reasonable when studying the descriptions and chemical analyses of Salmonsen & Tegner (2013). These estimates of granophyre content of the UZc and UZc’ (a total of 1.2 km³) are well below the total amount predicted (6–9 km³), suggesting that large amounts of granophyre may have been lost during the final crystallisation stages of the Skaergaard intrusion and may now reside in some of the associated granophyre lenses and sills.

5.12.5 Observed, predicted and ideal liquid lines of descent

The effects of immiscibility and selective migrating of the granophyric component in the mush pile of the LZ to UZa will markedly affect the observed liquid descent. In the following, we refer to three different calculated decent lines: ‘observed’, ‘predicted’ and ‘ideal’. The information obtained from the gabbro compositions are F_TMand D^*. These allow us to calculate the observed liquid descent line as the inverted melt compositions using Eq. (9). The ideal decent without granophyre loss can be calculated by perfect fractionation using Eq. (11). The lower part of the intrusion is modelled by perfect fractional crystallisation (LZ–UZa) and the upper part of the intrusion by equilibrium (or imperfect fractional) crystallisation (UZb–UZc; see Section 5.12.2). The predicted, or restored, liquid lines of descent can then be calculated by the perfect fractional or equilibrium crystallisation processes using Eq. (11) adjusted for the effects of formation of conjugate granophyre melt retained or lost from the mush as described below. The trace element concentrations in the conjugate melts are constants (Table 25), while the amount of trace elements lost from or added to the mush depends on the amount of trapped melt or the proportions of the conjugate melts. The predicted liquid lines of descent are thus an attempt to duplicate the observed compositions for which reasonable similarities or differences between these two decent lines reflect the success or failure of the calculations.

The granophyre component in the lower segment of the intrusion (below UZb) is considered to (1) be retained in the matrix of the gabbro, (2) migrate upward and enter the chamber as shown in Fig. 66, and (3) migrate laterally and coalesce in lenses and thus be lost from the mush by a non-mush representative sampling of the gabbro. We cannot distinguish between types (2) and (3) and thus group these together as lost or migrated granophyre. However, because we know the trapped-melt content (Table 24), we can use the constants in Table 25 to predict the ratio between the retained and lost granophyre and use a trial-and-error procedure to improve the model fit. In contrast to the LS below UZb, granophyre within the UZb and UZc magma-chamber granophyre migrated upward by variably increasing from zero at the base of the intrusion to 99% at the base of UZb. A portion is thus retained, and the rest is lost or otherwise not represented by the gabbros.

Fig. 67 shows the modelling results for three trace elements (Rb, Sc and Ba), based on the arguments outlined above by incorporating the effects of both interstitial liquid immiscibility and crystallisation (Fig. 65; Table 25). The lower part of the intrusion is modelled by Rayleigh fractionation (Eq. (11)) and the upper part of the intrusion by equilibrium crystallisation. Both segments were, in contrast to the traditional approach, modelled using a partially open system with a late-melt composition that is continuously changing due to liquid immiscibility-controlled migration of granophyre melt.

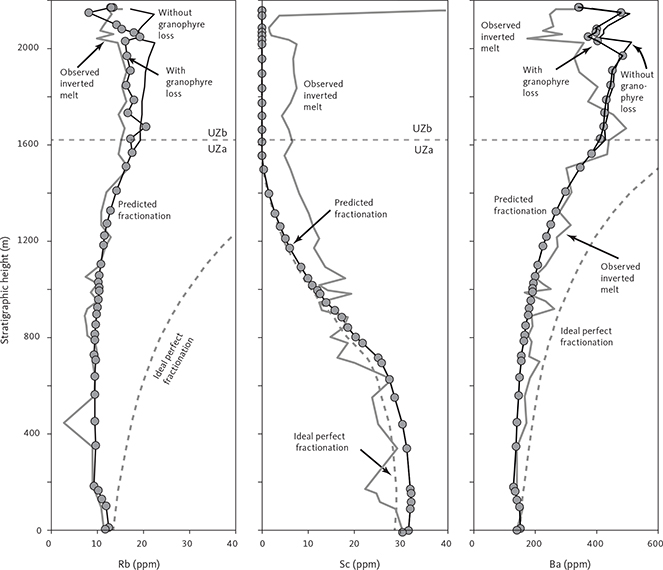
Fig. 67 Immiscibility models of Rb, Sc and Ba (ppm) shown as a function of stratigraphic height (m) in the LS. The observed inverted melt composition (solid grey curve) is for mass balance model A and C from Fig. 66. The ideal perfect Rayleigh fractionation (dashed grey curve) and the predicted fractionation (black curve with grey dots) are shown. The latter assumes that granophyre is lost from the LS column to either the upper zone chamber, or by migration out of the system to the UBS and into the intrusion host rocks or that the samples used here did not include granophyre. The lower part of the LS is modelled by Rayleigh fractionation (LZ–UZa) and the upper part as equilibrium crystallisation (UZb and UZc).

Rubidium is preferentially partitioned into the conjugate silicic melt (granophyre) during immiscibility and into the melt phase during fractional crystallisation (Table 25). The results for the lower sequence (LZ–UZa) are thus a good fit between the observed melt and the predicted compositions, while the ideal Rayleigh fractionation descent line deviates strongly from both the inverted melt and the predicted melt compositions (Fig. 67).

Scandium behaves in the opposite fashion of rubidium as it is preferentially partitioned into the immiscible basic melt and into the solid fraction during crystallisation (Table 25). Because of the very low scandium content, migration of granophyre will have indiscernible effects. The result is a reasonable, although not perfect, fit between the three observed and predicted descent lines (Fig. 67). The differences between the observed and the predicted fractional crystallisation may in the upper part of the sequence be attributed to the very low concentrations and high analytical uncertainty of scandium.

Barium is approximately evenly distributed between the two conjugate immiscible melts (Table 25) and, like rubidium, is strongly partitioned into the melt phase during crystallisation. The descent lines for barium show a reasonable fit between the observed and predicted curves only if a higher fraction of granophyre is retained in the gabbros (60%) than for rubidium (20%). It is possible that these marked differences may be related to shortcomings in the partition coefficients for barium.

Because the UZb–UZc chamber is modelled for equilibrium crystallisation, the scenario without granophyre migration would be expected to show little upward variation in trace elements in contrast to a loss of granophyre that would show an upward decrease in the elements that are preferentially partitioned into granophyre. This is consistent with rubidium that corresponds to the modelling for granophyre loss because of a preferential partitioning into granophyre. Barium evenly partitioned into the two cognate melts shows small differences between the models for loss of granophyre or without loss (Fig. 66).

The pooled granophyre loss from the LS amounts to 192 ppm Rb and 1158 ppm Ba (Sc < 1 ppm). Considering the sampling limitations (Table 18), these concentrations are comparable to some Skaergaard granophyre veins (Larsen & Brooks 1994; McBirney 1989a; Salmonsen & Tegner 2013), transgressive granophyres (Hirschmann 1992) and the Basistoppen granophyre (Naslund 1989).

Lastly, most studies have assumed that the two conjugate melts were unable to separate and that an emulsion persisted to temperatures well below 1060°C (Veksler et al. 2008; Jakobsen et al. 2011; Charlier & Grove 2012). The present study indicates partial separation and thus does not support a persistent emulsion in the UZ, where liquid immiscibility may have contributed markedly to the differentiation processes.

Several trace elements show a strong exponential increase approaching the final crystallisation fraction of the SH (e.g. Sc, Rb, Zn, Ba, REE, U; Figs 34, 35). Some of these terminal increases appear to be consistent with fractional crystallisation (Rb, Ba), while others may not (Sc; Fig. 67). McBirney (1995, 1996) argued that a late-stage buoyant liquid that is rich in volatiles and excluded elements rose from the upper part of the intrusion and permeated above the SH into the UBS to form a shadow SH horizon located slightly above the SH. McBirney and co-workers traced the origin of this to an observed decrease in Cl in apatite at the base of UZb and proposed the exsolution of a hydrous and chlorine fluid (Sonnenthal 1992; McBirney 1995) at about the level where liquid immiscibility was initiated. McBirney (2002) discussed the same observation and suggested that the increase in excluded elements was caused by a gradual change in partition coefficients due to volatile-saturated melts from the top of the MZ. However, Tegner et al. (2009) argued that the action of a Cl-rich fluid phase would have strongly fractionated Rb from U in contrast to the observations, and thus rejected any involvement of a fluid-saturated melt in the UZ.

5.12.6 Effects of granophyre migration on calculated trapped melt content

By incorporating the predicted granophyre loss, the restored gabbro compositions will markedly affect the calculated F_TM. This restored trapped-melt content is shown in Fig. 68 together with the corresponding bulk partitioning coefficients calculated by an iterative procedure and Eq. (12) for rubidium concentrations of the granophyre adjusted gabbro compositions (D_Rb^*). The D^* values for rubidium (and for Sc and Ba) were also used to calculate the liquid lines of decent shown in Fig. 67. The first-order result is a marked rise in F_TM upward, but in a pattern similar to that observed for calculations without granophyre adjustments (Fig. 61; Table 24). The adjusted trapped-melt content, reflecting the D_Rb^* variation, is about 40% in the LZa, decreases to 6% in the UZc, and subsequently increases to 20% at the top of the UZb, followed by an increase to high values at the SH (Fig. 68). We also observe that ideal Rayleigh fractionation at the UZa–UZb boundary reaches concentrations of about 25 ppm Rb, compared to about 80 ppm without granophyre adjustment. The subsequent crystallisation in the UZb and UZc does not change the rubidium concentration, which at the SH reaches an end-point concentration of about 30 ppm.

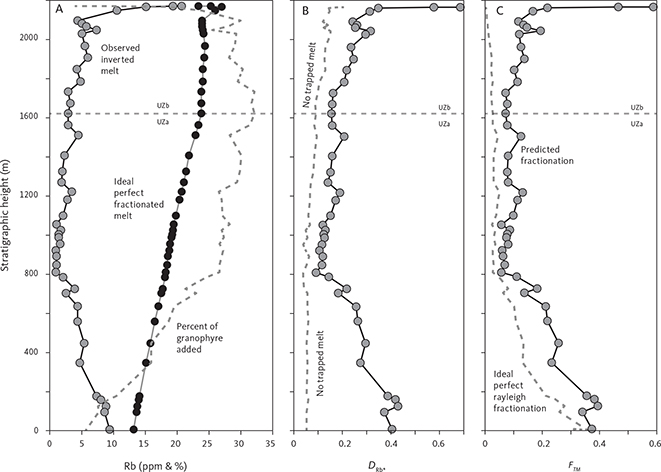
Fig. 68 Calculation of fraction of trapped melt (F_TM) as a function of stratigraphic height (m) in the LS, using mobile granophyre components and an adjustment of the fractionation modes. A: Observed inverted melt content of Rb (ppm), ideal perfect fractionated melt content of Rb (ppm), and the percent granophyre added to obtain the ideal fractionation curve. B: Bulk partitioning coefficients for Rb (D_Rb^*) compared to D_Rb^* values without trapped melt. C: The predicted F_TMobtained by adjusting the gabbro mush composition, restoring the gabbro to a mush composition after adding granophyre. The granophyre used in the modelling contains 40 ppm Rb (Table 18).

Tegner et al. (2009) assumed that the fractionation throughout the LS was controlled by Rayleigh fractionation and thus appear to have implied that the final product was granitic or granophyric. Our study suggests that the UZb and UZc crystallised by a process more similar to equilibrium crystallisation (or imperfect fractional crystallisation; Fig. 65). A similar observation was indirectly made by Namur & Humphreys (2018) based on primocryst-excluded trace element modelling. They observed good fits in their trace element modelling for UZb and UZc only if they used a trapped melt content of c. 60% (as opposed to c. 5% according to Tegner et al. 2009). This would drive the bulk-partitioning coefficient towards unity and supports a strong component of equilibrium crystallisation. Their observation of a high component of equilibrium crystallisation are not substantially different from the findings for the UZ in the present study. This would mean that gabbros in the upper part of the intrusion (UZb and UZc) change little in composition and thus allowed the final consolidated rocks to become a mixture of ferrodiorites mixed with migrated and coalesced granophyre lenses resulting from a UZb liquid immiscibility and the possible reactive products from the two components.

Several studies have attempted to quantify the thickness of the mush layer at the solid-melt interface using petrographic and microstructural observations for the Skaergaard intrusion (Namur et al. 2014; Nielsen 2016; Holness et al. 2017b, d; Vukmanovic et al. 2018) and the Bushveld Complex (Holness et al. 2017c, d; Kruger & Latypov 2020). Namur et al. (2014) showed that plagioclase-zoning profiles reflected the physical properties of the crystal mush and its porosity. Holness et al. (2017b) observed no correlation between estimated trapped melt and crystal plastic deformation in the centre of the Skaergaard intrusion, leading them to propose that compaction had been of minor importance and that the magmatic fabric reflected a thin layer of primary mush. Holness et al. (2017b) further evaluated the mush thickness at the appearance of apatite at the UZa–UZb boundary. They used microstructural step-changes in the latent heat accompanying the appearance of apatite to suggest that the mush thickness in the centre and eastern parts was only a few metres thick, increasing to c. 100 m in the western part of the intrusion (all at the UZa–UZb boundary). Similar studies of the Rustenburg layered suite of the Bushveld Complex (Holness et al. 2017d) suggest a mush thickness of the order of a few metres and that neither gravitationally driven compaction nor compositional convection were likely to have been important processes during solidification. It was also suggested that adcumulates are most likely formed at the top of the mush during primary crystallisation. Furthermore, gabbro blocks were believed to have detached from the roof zone and sink through the melt reservoir to rest on the contemporaneous mush (Irvine et al. 1998; Sonnenthal & McBirney 1998). These blocks range from a few centimetres to several hundred metres in size. They are regarded to have indented the bottom mush on impact and are overlain by subsequent draping layers. This suggests a well-defined interface between the melt reservoir and the solid gabbro substratum and a thin mush zone (Irvine et al. 1998).

In conclusion and paraphrasing Holness et al. (2017d) and Holness (2018), the main issue with some of these arguments is that they are often based on bulk geochemistry and an arbitrary model of fractionation involving primocrysts and an interstitial trapped liquid. This interstitial liquid is now thought likely to have undergone significant in situ fractionation, including the preferential loss of at least one immiscible component. Until we can quantify the amount of interstitial liquid and its fate, our understanding of the post-cumulus evolution of layered mafic intrusions will remain uncertain. One possible way forward is to characterise plagioclase overgrowths and their relationship to the volume of interstitial melt (Maaløe 1976a; Toplis et al. 2008, Namur et al. 2014; Nielsen et al. 2015; Namur & Humphreys 2018).

5.13 Summary of solidification models

Fractional crystallisation is widely thought to have occurred during the solidification of the Skaergaard magma chamber (Wager & Deer 1939; McBirney 1989a, 1995), particularly as recorded in the major elements and the systematic variation in mineral compositions (e.g. Figs 25, 26). Perfect fractional crystallisation, modelled by Rayleigh equations, however, fails to reproduce the observed variations specifically for the excluded trace elements (low D^*). Meanwhile the included trace and the major elements (high D^*) are in many cases a better fit (Figs 60, 62). The main obstacle to understand the solidification of the Skaergaard intrusion is therefore, that this observation suggests a decoupling of the excluded and included trace elements, meaning that identical fractionation processes cannot model the two groups of trace elements.

Perfect fractional crystallisation is an end-member model that probably rarely operates in magma chambers where solidification is occurring from the top-down, bottom-up and sides-inward. In such a chamber, mush zones are present to a varying extent, and the efficiency of crystal-liquid separation is strongly controlled by the orientation of the solidification front and gravitational forces. Under such variable conditions, the overall evolution would be delayed relative to that predicted for perfect fractional crystallisation. Crystallisation is ultimately controlled by partition coefficients and phase equilibria governing crystallisation in a convecting and homogenising magma. The resultant solid substratum or crystal-melt mush is thus made up of minerals and melt in equilibrium with the main magma. In contrast, in situ (or bottom) crystallisation assumes crystallisation in a boundary mush layer or directly on a solid substratum, which is only in part equilibrated with the main magma and may thus be controlled by phase equilibria and bulk partitions that are different from those of the main magma chamber. The case for in situ fractionation of the Skaergaard intrusion is preferred by Nielsen et al. (2015) and Nielsen (2016) based on the concentric form of the intrusion (Nielsen 2004), the evidence for the presence of abundant interstitial melt-mineral reactions (Holness et al. 2011) and liquid immiscible droplets (Jakobsen et al. 2011). However, for in situ crystallisation to be a viable possibility, the amount of required melt remaining in the mush must greatly exceed the predicted amounts (Fig. 61; Table 24). This indicates that either fractional crystallisation and compaction were the likely processes dominating the solidification or, as suggested by this study, that the predictions of the trapped-melt content are greatly underestimated (Fig. 68; see also McBirney 1995; Tegner et al. 2009).

The effects of liquid immiscibility on the terminal fractionation of the intrusion offer a mechanism by which to explain the decoupling of the included and excluded trace elements. By formulating simple models (Figs 65, 66) that invoke migration and loss of granophyre melts formed from immiscibility initiated at the base of the UZb and likewise in the trapped interstitial melt, reasonable correspondence between perfect Rayleigh fractionation and observed or inverted melt compositions can be obtained (Fig. 67). This modelling works for at least some trace elements for which partition information is available and requires upward migration from the LZ and UZa into the main chamber as well as lateral migration. The main chamber at the UZb and UZc levels (the final 10%) is viewed as a zoned chamber with restricted convention or no convention, and it is suggested that granophyre melt is lost to the UBS and surroundings in the form of granophyre sills.

Liquid immiscibility near the end-stages of solidification may have resulted in the stagnation and possible stratification of the residual magma that suppressed efficient crystal-melt segregation, a process that had dominated the evolution of the main magmatic system up to that point. Another consequence is that the Skaergaard intrusion solidified with significantly higher amounts of trapped melts than predicted by Tegner et al. (2009) and summarised in Table 24. This would have resulted in an upper part (UZb, UZc) where the trapped-melt content might have reached high values approaching the SH horizon (Fig. 68).

6 Concluding remarks

A sound knowledge of the amount of trapped melt in the gabbro mush is crucial for understanding the solidification of the Skaergaard magma chamber, including thermal and temporal cooling, the liquid line of descent, trace element partitioning and textural and mineralogical variability of the late-stage solidification of the gabbros. It is nevertheless apparent from the present study that such information is uncertain at best. The amount of trapped melt is calculated using excluded trace elements (like Rb) analysed in the gabbros and normalised to the predicted concentration in the melt assuming perfect fractional or equilibrium crystallisation. Only if the analysed gabbros represent the final gabbro mush and the crystallisation mode is sufficiently understood, will this method of calculation yield the correct result.

Tegner et al. (2009) assumed that the analysed samples represented the final mush gabbro and that the mode of crystallisation was approximated by Rayleigh fractionation. The main drawback of these assumptions is that for extreme crystallisation with little remaining melt (F → 0), the trapped melt will always go to zero, irrespective of any actual observations to the contrary, such as the presence of interstitial granophyre. This is because the concentration of a highly excluded trace element will go to very high values when F goes to zero, assuming perfect fractional crystallisation. Despite these shortcomings, particularly for the UZb and UZc, the procedure of Tegner et al. (2009; Fig. 61) has provided baseline calculations of the trapped-melt content used here and in other studies (e.g. McKenzie 2011; Holness et al. 2017b).

The mobility of a late-stage granophyric melt in the Skaergaard mush has nevertheless, directly or indirectly, been acknowledged in the past (e.g. Wager & Brown 1967; Naslund 1989; Larsen & Brooks 1994; Jakobsen et al. 2011) and has been built into summation modelling of the initial or final composition and the liquid descent line (Tegner 1997; Nielsen et al. 2009; Andersen 2006). This has often been done without considering the implications of a missing granophyre or melanogranophyre component.

A critical observation in the present study is that the excluded trace elements are decoupled from the included trace (and major) elements and thus cannot be explained by identical differentiation mechanisms (Figs 62–64). A crystallisation model (Figs 65, 66) illustrates the potential effects of liquid immiscibility in the trapped melt as well as in the overall magma chamber that is inferred to be initiated at the UZa–UZb boundary or equivalent in the mush melt. Using this model, it is possible to predict the evolution of both the included and the excluded elements for identical crystallisation modes (Fig. 67). The requirement is that a granophyre component would have migrated upwards and laterally in the intrusion and, thus be partly lost from the sampled and analysed mush gabbros. These observations imply that the gabbro mush samples used here and in previous studies (e.g. Tegner et al. 2009) may underestimate the actual trapped-melt component unless adjusted for these lateral and horizontal granophyre migrations.

The differences between rubidium concentrations of the observed and the predicted modelling by perfect or imperfect fractional crystallisation without granophyre loss can be used to adjust the gabbro to its possible original composition (using c. 65 ppm Rb in granophyre; Table 18). The granophyre predicted to have been lost from the gabbros are shown in Fig. 68A ranging from small amounts in the LZa (c. 5%), raising fast to 25% in LZc, then further raising to 30% at the base of UZb, subsequently decreasing to 25% at the base of UZc, and thereafter dropping to low values (Fig. 68A).

The fundamental requirement for bottom solidification processes is the operation of a convecting and homogenising magma chamber concurrently with the growth of the solid mush along the margins and the expulsion of evolved melt, whether resulting from compaction or convective wall processes (Wager et al. 1960; Maaløe 1978; Morse 1986; McBirney 1995). It is the convection and homogenising of the main chamber that drives the systematic cryptic variation seen in the LS and UBS (Figs 25–29). Wager & Brown (1967, p. 206) thought that the magma was essentially stationery during the formation of the so-called tranquil division of the MBS and subsequently became convective with the appearances of prominent banding. Maaløe (1976a, 1987) placed the onset of large-scale convection in the chamber to about 35 m height in the Cambridge Drill Core, approximately at the base of the LZa. At this point, he observed a significant drop in plagioclase composition and change in zoning pattern. Holness et al. (2015) also examined the Cambridge Drill Core and suggested a pulsed filling of the lower parts (HZ), followed by a rapid ballooning of the chamber commencing in LZa, and by the onset of chamber-wide convention (cf. Holness et al. 2007a).

Chamber-wide convection driven by cooling is believed to have persisted until the UZa–UZb boundary. At this point, about 400 m of chamber remained in the central part of the intrusion (Fig. 30), the melt composition may have reached an andesitic composition with about 62 wt% SiO₂ (Fig. 44), and has seen a dramatic increase in viscosity to 7000 Pa·s (for a dry Si-enrichment descent line; Fig. 59). Rhythmic layering reaches a maximum intensity in the UZa, subsequently ceases in UZb, and is largely not recognisable in UZc (Wager & Deer 1939; Wager & Brown 1967; McBirney & Noyes 1979; Irvine 1987). An effect of the homogeneous nature of UZb without prominent layering is the restricted modal and compositional variability observed in the bulk rock and primocryst of the samples from drill core 90-22 (Figs 15, 25–27).

Holness et al. (2007b) observed a cessation in grain boundary adjustments in the UZb gabbro at about the same time as modal and grain-size layering became less prominent. They discussed these observations as the result of either a transition from convective to conductive heat transfer or to the cooling below the closure T for pyroxene-plagioclase grain boundary migration. Namur & Humphreys (2018) modelled the trace element contents in plagioclase and clinopyroxene to be broadly consistent with efficient fractional crystallisation until the lower part of UZa (F ≈ 0.20). Above this stratigraphic level, they proposed that fractional crystallisation became less efficient and was replaced predominantly by equilibrium crystallisation.

Our findings show that the UZa–UZb boundary (c. 1060°C, F = 0.10) marks the onset of liquid immiscibility in the main chamber. This is supported by the modal variation (Figs 15, 51) and the phase equilibria (Fig. 47). Based on a study of gabbro compositions, it is observed that the included and excluded trace elements are decoupled throughout most of the LS. Only the included elements (thus also the major elements) can reasonably be modelled by fractional crystallisation (Figs 62, 64). The apparent decoupling of included and excluded trace elements may arise from difficulties obtaining gabbro samples that represent the true final mush. The residual trapped melt in the mush cools in situ either isolated or by reactions with the primocrysts. It may thus reach saturation at 1060°C of two conjugate immiscible melts of which the basic melt is likely to remain in place and the silicic, or granophyric, melt may raise or otherwise migrate in the mush (Fig. 59), possibly into the main chamber reservoir. The granophyre content lost from the gabbro mush increases with decreasing overall temperature.

If the gabbro compositions are restored to their assumed residual mush compositions by adding a granophyre melt composition, it is possible to restrain the melt composition to perfect Rayleigh fractionation into the UZb (Fig. 66). This way, crystallisation can explain both the included and the excluded elements by fractional crystallisation in the lower part and by equilibrium in the upper part of the intrusion. The result is that the two trace element groups are no longer seen as being decoupled (Fig. 67). Namur & Humphreys (2018) supports this conclusion. They used in situ trace element analyses of coexisting mush minerals without directly using the gabbro compositions, and reached the conclusion that the LS, until the lower part of UZa, was controlled by fractional crystallisation after which they suggested an increasing component of equilibrium crystallisation.

The adjusted trapped-melt content reaches high values in UZ (Fig. 68), which could significantly have changed the overall differentiation pattern and the behaviour of the mush. A smaller amount of melt would in the case of in situ fractionation have returned to the main chamber and consequently have dampened the fractionation effect and resulted in a better balancing of the included and the excluded elements (Fig. 64). Values of D^* would have decreased (included elements) or increased (excluded elements) towards unity (→ 1) and have dampened the extreme modelled compositions for Rayleigh fractionation (Fig. 67). Because a larger amount of melt was retained in the mush, another effect would have been that the gabbro column with stratigraphic height would have moved more rapidly towards low remaining melt content (F → 0). Since the calculations of the adjusted trapped-melt content were based on Rayleigh fractionation, it is not possible to further evaluate the relative contributions of perfect, imperfect, or in situ fractionation to the overall differentiation of the Skaergaard intrusion. To gain better insight into the details of the differentiation process, independent estimates of the amount of trapped mush melt are required.

Most studies, including ours, would argue that fractional crystallisation controlled by in situ crystallisation and a major chamber homogenised by convection explains the observed differentiation in the LS (cf. McBirney & Noyes 1979; Namur & Humphreys 2018). Based on modelling of a simplified basalt system (haplobasalt), Maaløe (1976b) suggested that Rayleigh fraction dominated, but argued for a component of imperfect fractionation (partial fractionation) to explain the delayed fractionation of plagioclase. Nielsen et al. (2015) advocated for dominant in situ fractionation in the final stages of crystallisation and formation of the PGE and gold deposit in what is commonly referred to as the Triple Group of the upper part of the MZ. They have extended this idea to the entire intrusion (Nielsen 2016) but have not provided substantial documentation and arguments for in situ fractionation as opposed to other modes of fractionation. Higher volumes of interstitial mush melt would be present when reached the onset of liquid immiscibility at about 1060°C. Consequentially, at this point the interstitial melt would still be present, perhaps forming an interconnected network that would better allow the buoyant migration of the silica-rich immiscible conjugate melt.

The same observations may also provide insight into the local and large-scale metasomatic reactions proposed by McBirney and coworkers (McBirney 1989a, 1995, 2002; McBirney & Sonnenthal 1990; Sonnenthal & McBirney 1998). McBirney (1996) writes that “[..] a buoyant liquid, rich in volatiles and incompatible elements, rose from the LS and permeated the upper part of the intrusion.” He attributed such an upward flux of reactive aqueous liquid or fluid in the LS mush to the observed pervasive infiltration metasomatism (McBirney & Sonnenthal 1990), as well as to the overall decoupling between excluded and included elements (McBirney 1989a, 2002). Specifically, Sonnenthal (1992) interpreted evidence from Cl/F ratios of apatite, biotite, and amphiboles in the UZa to the exsolution of an aqueous Cl-rich fluid (McBirney 1995). Changes in the apatite Cl/F ratio was also observed in this study suggesting the exsolution of a Cl-rich fluid at the UZa–UZb boundary, followed by a second exsolution of a water-rich fluid at the UZb–UZc boundary (Fig. 24B). McBirney (2002) used a larger set of apatite analyses to place the initiation of the exsolution of a Cl-rich fluid to the upper part of the MZ. Later work by Pedersen et al. (2021), however, was unable to define the horizon where a potentially Cl-rich fluid might have exsolved.

The implications of the present study are that (1) compaction was restricted, (2) solidification occurred in a boundary-layer mush containing variable amounts of interstitial melt, (3) it was possible for a late-stage silica-rich conjugate immiscibility melt to migrate and raise from the mush while a Fe-rich conjugate melt had limited ability to sink or was retained at the level of formation, (4) a prolonged upward migration of buoyant silicic melt into the main chamber was possible, and (5) final solidification of the mush package, after termination of immiscibility, was controlled by cooling to, or below, a closure temperature of c. 950°C. This scenario possesses some similarities to the suggestion by McBirney (2002).

Complications arise from crystallisation of interstitial melt in pore spaces and the possibility of an upward migrating, reacting and crystallising melt (McBirney 1998, 2002) that is not well understood. Tegner et al. (2009) argued that compaction of the primocryst pile preceded the growth of interstitial trace element enriched minerals. Some migration of interstitial basaltic melt from the trapped mush likely occurred (Humphreys 2009; Holness et al. 2011; Holness 2018; Namur et al. 2014), although such migration is believed to have had restricted impact. Another factor at play may be compositional convection and exchange in a boundary zone of evolved mush melts with less-evolved magma chamber melts. This would result in constant composition of mush melt and thus an effective buffering of mineral compositions, eliminating trapped melt and interstitial crystallisation (Wager et al. 1960; Irvine 1980; Morse 1986). Tegner et al. (2009) and Namur et al. (2014) have argued against such a possibility as a dominating factor for the Skaergaard intrusion. They argue that given that very similar rock textures are universally and simultaneously developed in gabbro of the floor, walls, and roof of the intrusion, this is unlikely to be due to a gravitationally driven process of convection, but more likely to have been caused by compaction. Additional processes are thus required to explain the observed excluded elemental deficiency compared to the predicted composition expected for perfect fractional crystallisation, including upward migration of a late-stage silicic melt from the intrusion due to compaction and density differences into the UBS and host rocks. McBirney (2002), nevertheless, preferred upward elemental migration aided by an exsolved chlorine-rich, hydrous fluid from the MZ and above that eventually escaped from the intrusion with its load of excluded elements.

Acknowledgements

The ICP-MS trace element analyses were done by Eric Brown and Michelle Gras at the Interdisciplinary Center for Plasma Mass Spectrometry, University of California, Davis. The major element XRF analyses were done by Sidsel Grundvig at Department of Geoscience, Aarhus University. The fluorine analyses were done by Ole Stecher while at University of Copenhagen’s Arctic Station in Qeqertarsuaq, Disko, Greenland. The electron microprobe analyses were done at the Department of Earth and Planetary Science, University of California, Davis, and at the Department of Geoscience, Aarhus University. Jakob Keiding previously analysed some of the UZc samples used here by electron microprobe in Aarhus and completed gabbro density measurements. We are indebted to many more people who over the years have helped and enlightened our understanding of the Skaergaard intrusion by always being willing to discuss even the most ephemeral subjects and to read our various nascent manuscripts. They include Troels Nielsen, Kent Brooks, Gry Barfod, Rune Larsen and Harry Esbensen. The final manuscript benefitted from critical comments from the editor Jakob Kløve Keiding and from the reviewers Ilya Veksler and Rais Latypov. The Bulletin editor Catherine Jex and her team greatly contributed to the final version of our manuscript. It is a special pleasure to be able to dedicate our work to Alex McBirney and Neil Irvine whose work on the Skaergaard intrusion has been a constant inspiration. We must, however, take the full responsibility for any shortcomings in the present presentation and interpretations.

Additional information

Author contributions

All authors equally contributed to the conceptual ideas and formulation of research goals and planning and completion of the fieldwork. PT developed the methodology and models and wrote the original draft and presentation of the result, while all authors contributed to the final review and editing. CT curated the field collected samples. CEL acquired the main funding for the analytical aspects leading to this publication.

Additional files

Included in this manuscript are three appendices: Appendix 1. History of exploration, Appendix 2. Sampling methods and reference profile construction and Appendix 3. Analytical methods.

Supplementary Files are available to download at https://doi.org/10.22008/FK2/UTFJP4. Supplementary file S1: Excel spreadsheet with summary of gabbro and mineral compositions. Supplementary files S2: Excel spreadsheets of all tables. Supplementary files S3: Forward modelled liquid lines of descent (Tables S1, S2). Supplementary files S4: Plane-polarised microscope images of thin sections. Supplementary files S5: Classic sample location maps. Supplementary files S6: Geological maps. Supplementary files S7: Topographic maps. Supplementary files S8: Stereoscopic Aerial Colour Photos (1:27 000). Supplementary file S9: Sample repositories.

References

Appendix 1 History of exploration of the Skaergaard intrusion

The Skaergaard intrusion was discovered in 1930 by L.R. Wager as a member of the British Arctic Route Expedition (Chapman 1932; Watkins 1932). The first aerial photos of the intrusion were made during this expedition and were later used by Wager & Deer (1939) for mapping purposes. Wager returned in 1932 to the area as part of an Ejnar Mikkelsen expedition (Mikkelsen 1933) exploring the district between Ammassalik Ø (Tasiilaq) and Scoresby Sund (Ittoqqortoormiit; Wager 1934, 1935, 1947). Wager returned in 1935 to the Kangerlussuaq fjord (central East Greenland), specifically to study the Skaergaard intrusion, and overwintered in Hjemstedbugt (Homestead Bay) on the intrusion with a small party, including his wife Phyllis and W.A. Deer (Deer 1967a; Brooks 1985, 1990; Hargreaves 1991). The outcome of this overwintering was the seminal monograph on the Skaergaard intrusion that appeared only three years later (Wager & Deer 1939). The interest was so strong that an unprecedented second amended version was issued in 1962. The years 1934–1972 saw several additional monographs published in the East Greenland series of Meddelelser om Grønland based on results obtained during the British East Greenland Expeditions increasing the total published monographs to 10.

The intrusion saw little activity during World War II, except for the establishment of a weather station in 1945 on Skærgårdshalvø, later transferred to Aputiteeq. Wager and Deer returned in 1953 to the Kangerlussuaq fjord to collect further samples from the Skaergaard intrusion as well as for other mapping objectives in the area (Wager 1954). New samples were needed, mainly due to rapid depletion of the original existing material from the numerous mineralogical and geochemical investigations that had since been conducted. Wager incorporated this new information in a long chapter on the Skaergaard intrusion included in a book on ‘Layered Igneous Rocks’ written and edited by himself and G.M. Brown (Wager & Brown 1967) that also included an updated version of the initial map from the 1939 monograph. This book was published in the US by W.H. Freeman of San Francisco in 1967 and the following year in 1968 by Oliver & Boyd of Edinburgh, United Kingdom.

To investigate the unexposed basal parts of the intrusion (i.e. the Hidden Zone; HZ), drilling was essential and preparation was underway in the 1960s. The untimely death of Wager in late 1965, prior to the publication of the layered intrusion book, left the drilling plans to be concluded by W.A. Deer, who returned to Skaergaard the following year (Deer 1967b). This drilling resulted in a total of 588 m of core collected from two sites penetrating gabbro (referred to as the Cambridge Drill Cores). The only part of these drill cores that has been studied to some extent is core I, which penetrated 349 m into basal gabbros of the intrusion, including c. 150 m of unexposed stratigraphy (e.g., Maaløe 1976; Nwe 1976; Holness et al. 2015).

UK scientific interests in the Skaergaard ceased with the Cambridge drilling and the activities shifted to US groups mainly lead by A.R. McBirney (Oregon University), who organised several expeditions between 1971 and 1984 (e.g. Naslund 1984; Hoover 1989; McBirney 1989a). This field work led to the compilation of the third and most recent geological map of the Skaergaard intrusion in 1989 (McBirney 1989b). The supplementary material includes scans of all the known geological maps.

Concurrently, C.K. Brooks (University of Copenhagen) organised expeditions to the Kangerlussuaq area between 1972 and 1991, mainly focused on regional tectono-magmatic aspects, but also included studies of Skaergaard on several occasions (Larsen & Brooks 1994; Brooks 2018). T.N. Irvine of the Carnegie Institution for Science, Washington, participated in several of these expeditions over the years and published extensively on the origin of the layering of the intrusion (e.g. Irvine et al. 1998). D.K. Bird from Stanford University, California, was also part of these activities (Bird et al. 1986).

Aerial photography by the Danish Geodetic Institute was completed in 1975 eventually leading to a new, improved topographic map of the intrusion used by McBirney and later investigators. See Supplementary Files S7 for the topographic maps and Supplementary Files S8 for high-resolution scans of the aerial photos used in this mapping.

Commercial exploration activities on Skaergaard were initiated in 1986 with the discovery of a gold-palladium mineralisation (e.g. Bird et al. 1991). Several drill cores, mostly through the upper part of the intrusion, were completed by Platinova Resources Ltd during 1989–1990 (Watts, Griffis & McQuat Ltd 1991). Some of these cores had been made available for research from an outdoor storage site near the intrusion (e.g. Tegner 1997; Andersen et al. 1998). Subsequently, the commercial interest in the Skaergaard mineralisation was transferred to Skaergaard Minerals Corporation, who conducted further drilling and sampling that culminated in 2004 (Hanghøj 2005). See the summary of sample repositories in the Supplementary File S9 for the availability of Skaergaard samples. Despite that To date, several companies have been involved in the exploration activities on the Skaergaard intrusion, which were still ongoing at the time of writing. Despite this, no attempt has been made so far to mine the deposit, mainly due to the high cost of mining in the Arctic.

The scientific interest expanded when parties from the Danish Lithosphere Centre’s campaign on the East Greenland rifted margin visited the intrusion in 1995 and 2000 (Nielsen et al. 2001). Several of the exploration drill cores from temporary outdoor storage in Greenland were as a result transferred to permanent storage in Copenhagen (Nielsen et al. 2000). A UNESCO International Geoscience Programme field conference on site at the Skaergaard intrusion was held in September 2001 organised by J.C.Ø. Andersen and C.K. Brooks. Following the conference, a ‘virtual’ Skaergaard intrusion website has been maintained by J.C.Ø. Andersen (http://www.skaergaard.org). Brooks (1997, 2018) has published extensive and very useful accounts of the exploration of the Skaergaard intrusion, including an annotated literature list with selected abstracts.

Most recently, groups from the University of Aarhus (Denmark), Cambridge University (UK), and University of California Davis (USA) continued work post 2000 on the Skaergaard intrusion, both in laboratories and the field. Part of these activities occurred concurrently with the renewed exploration drilling activities by Skaergaard Minerals Corporation (Hanghøj 2005). The present work is one of many outcomes of these recent efforts.

Wager & Deer’s 1939 monograph has significantly shaped the theory of igneous petrology since it was first published. In 1939, the theory of magmatic differentiation and fractional crystallisation were being formulated and the common basalt liquid lines of descent discussed (Wilson 1993; Young 1998, 2003). N.L. Bowen at the Geophysical Laboratory in Washington dominated this debate and advocated a Si-enrichment trend principally based on experimental observation (Bowen 1928). The most prominent dissenting voice was C.N. Fenner also at the Geophysical Laboratory that based his arguments for the existence of an Fe-enrichment trend on field observations (e.g. Fenner 1929). When Wager & Deer’s 1939 Skaergaard study was published it landed squarely in the middle of this discussion by presenting a well documented example of what was seen as an Fe-enrichment trend in an extreme differentiated pluton. It provided the foundation for understanding fractional crystallisation, convecting magma chambers and the origin of layering in igneous plutons. However, it is perhaps a tribute to the complexities of understanding the details of the Skaergaard intrusion that the debate of Si-enrichment vs. Fe-enrichment trends (or Bowen vs. Fenner trends) still reverberate in the discussions and that this issue has not yet been satisfactory solved (Hunter & Sparks 1990). Although our understanding today may have changed on some points, the foundation provided by Wager & Deer (1939) is still valid and still forms a central part of all igneous petrology textbooks (e.g. Carmichael et al. 1974; Hess 1989).

References

Appendix 2 Sampling methods and reference profile construction

The new reference profile is constructed using drill core samples through the UZa and UZb and into the upper part of the MZ and surface samples extending the coverage of the LS into the LZa and the UZc, including the SH and the adjoining part of the UBS.

Between 1986 and 1990, Platinova Resources Ltd. conducted an extensive mineral exploration program on the Skaergaard intrusion focusing on the potential for precious metal deposits in the LS. A series of exploration diamond drillings were completed in 1989 and 1990 for which the drill cores were stored outside near a small aircraft landing field in Sødalen. In 1999, the responsibility for this material was transferred to the GEUS. Funding from the Danish Natural Science Research Council and Greenland Bureau of Mines and Petroleum provided the opportunity to retrieve selected cores during the 2000 field season. The cores totalled 4308 m and were considered to be of greatest scientific importance (Nielsen et al. 2000, 2001). These cores are now curated by the Geological Museum at the University of Copenhagen, Denmark (Appendix A2.1). In this study, we only use samples from Hole 90‑22 that traverses the MZ to UZa boundary and penetrated below the Triple Group in the MZ. Hole 90-22 represents 1052 m of gabbros from which 51 representative samples were selected (Appendix A2.2).

Appendix 2.1 Platinova drill cores airlifted to Copenhagen in 2000

Drill core no.	Depth	Azimut	Inclination	Altimeter	UTM		Interval
	(m)			(m)	E	N	shipped (m)
90–10	535	300	–70	2	552374	7560758	0–535
90–18	1026	320	–70	59	553403	7560044	0–1026
90–22	1052	340	–70	306	554604	7561147	0–1052
90–23	843	35	–70	577	557884	7561597	218–569
90–23a	842	35	–70	577	557884	7561597	559–841
90–24	1072	0	–70	502	555066	7561739	0–1072
Total							4318

 

Appendix 2.2 Position and stratigraphic height of samples in the LS, Skaergaard intrusion

Sample ID a	Stratigraphic	Zone/	Profile section	Rock type	Altitude c	Latitude d		Longitude d		UTM e		F f	T g
	position (m) b	Subzone			(m)	°	‘	°	‘	E	N		(°C)
458633	2169	UBS	Basistoppen	gabbro	499	68	9.67	–31	40.03	555325	7561425	0.000	1012
458634	2168	UBS	Basistoppen	gabbro	499	68	9.67	–31	40.03	555325	7561425	0.000	999
458635	2165	UBS	Basistoppen	gabbro	494	68	9.66	–31	40.01	555343	7561409	0.000	955
458636	2165	UZc	Basistoppen	gabbro	494	68	9.66	–31	40.01	555343	7561409	0.000	995
458637	2165	UZc	Basistoppen	gabbro	493	68	9.66	–31	40.01	555343	7561409	0.000	993
458638	2165	UZc	Basistoppen	gabbro	492	68	9.66	–31	40.01	555343	7561409	0.000	1006
458639	2165	UZc	Basistoppen	gabbro	491	68	9.66	–31	40.01	555343	7561409	0.000	1005
458640	2164	UZc	Basistoppen	gabbro	489	68	9.66	–31	40.01	555343	7561409	0.001	1001
458641	2164	UZc	Basistoppen	gabbro	488	68	9.66	–31	40.01	555343	7561409	0.001	1008
458642	2163	UZc	Basistoppen	melanogabbro	493	68	9.66	–31	40.01	555343	7561409	0.001	994
458643	2150	UZc	Basistoppen	gabbro	484	68	9.67	–31	40.03	555325	7561425	0.002	997
458644	2147	UZc	Basistoppen	gabbro	478	68	9.67	–31	40.08	555291	7561422	0.003	1006
458645	2144	UZc	Basistoppen	gabbro	473	68	9.67	–31	40.11	555275	7561420	0.003	1003
458646	2144	UZc	Basistoppen	gabbro	472	68	9.67	–31	40.11	555275	7561420	0.003	1007
458647	2141	UZc	Basistoppen	gabbro	468	68	9.67	–31	40.18	555227	7561425	0.003	1008
0.7	2091	UZc	Core 90-22-0.7m	gabbro								0.010	1017
458652	2089	UZc	Basistoppen	gabbro	442	68	9.75	–31	40.74	554835	7561559	0.010	1020
10.6	2081	UZc	Core 90-22-10.6m	gabbro								0.011
458653	2075	UZc	Basistoppen	gabbro	423	68	9.75	–31	40.83	554774	7561558	0.012	1022
20.8	2071	UZc	Core 90-22-20.8m	gabbro								0.013	1013
31.1	2061	UZc	Core 90-22-31.1m	gabbro								0.014
40.9	2051	UZc	Core 90-22-40.9m	gabbro								0.015	1022
46.2	2046	UZc	Core 90-22-46.2m	gabbro								0.016
47.4	2044	UZc	Core 90-22-47.4m	gabbro								0.016	1014
458654	2032	UZc	Basistoppen	gabbro	401	68	9.79	–31	40.91	554711	7561631	0.018	1020
458657	2030	UZc	Basistoppen	melanogabbro	391	68	9.77	–31	41.02	554638	7561607	0.018	1028
458658	2030	UZc	Basistoppen	melanogabbro	391	68	9.77	–31	41.02	554638	7561607	0.018	1000
67.6	2024	UZb	Core 90-22-67.6m	average gabbro								0.019	1025
87.7	2004	UZb	Core 90-22-87.7m	average gabbro								0.022	1028
107.7	1984	UZb	Core 90-22-107.7m	average gabbro								0.025	1024
129.6	1962	UZb	Core 90-22-129.6m	average gabbro								0.029	1025
149.8	1942	UZb	Core 90-22-149.8m	average gabbro								0.032	1030
170.4	1921	UZb	Core 90-22-170.4m	average gabbro								0.036	1028
189.9	1902	UZb	Core 90-22-189.9m	average gabbro								0.039	1030
210.9	1881	UZb	Core 90-22-210.9m	average gabbro								0.043	1032
229.4	1862	UZb	Core 90-22-229.4m	average gabbro								0.046	1029
249.2	1843	UZb	Core 90-22-249.2m	average gabbro								0.050	1039
270.3	1822	UZb	Core 90-22-270.2m	average gabbro								0.054	1034
290.8	1801	UZb	Core 90-22-290.8m	average gabbro								0.058
310.2	1782	UZb	Core 90-22-310.2m	average gabbro								0.062	1033
323.8	1768	UZb	Core 90-22-323.8m	average gabbro								0.065
344.1	1748	UZb	Core 90-22-344.1m	average gabbro								0.069	1035
364.1	1728	UZb	Core 90-22-364.1m	average gabbro								0.073	1039
384.0	1708	UZb	Core 90-22-384.0m	average gabbro								0.077	1041
401.3	1691	UZb	Core 90-22-401.3m	average gabbro								0.081
421.0	1671	UZb	Core 90-22-421.0m	average gabbro								0.086	1038
441.7	1650	UZb	Core 90-22-441.7m	average gabbro								0.090	1043
461.8	1630	UZb	Core 90-22-461.8m	average gabbro								0.095	1040
471.8	1620	UZa	Core 90-22-471.8m	average gabbro								0.097
481.8	1610	UZa	Core 90-22-481.8m	average gabbro								0.100	1044
491.8	1600	UZa	Core 90-22-491.8m	average gabbro								0.102	1047
530.9	1561	UZa	Core 90-22-530.9m	average gabbro								0.112	1045
555.5	1536	UZa	Core 90-22-555.5m	average gabbro								0.118
565.3	1527	UZa	Core 90-22-565.3m	average gabbro								0.120	1055
585.8	1506	UZa	Core 90-22-585.8m	average gabbro								0.126	1053
648.4	1443	UZa	Core 90-22-648.4m	average gabbro								0.143	1056
660.6	1431	UZa	Core 90-22-660.6m	average gabbro								0.146
689.1	1403	UZa	Core 90-22-689.1m	average gabbro								0.154	1058
729.2	1363	UZa	Core 90-22-729.2m	average gabbro								0.166	1062
749.2	1343	UZa	Core 90-22-749.2m	average gabbro								0.171
769.1	1323	UZa	Core 90-22-768.1m	average gabbro								0.177	1056
789.7	1302	UZa	Core 90-22-789.7m	average gabbro								0.184	1061
809.7	1282	UZa	Core 90-22-809.7m	average gabbro								0.190	1064
824.2	1268	UZa	Core 90-22-824.2m	average gabbro								0.194
844.0	1248	UZa	Core 90-22-844.0m	average gabbro								0.201	1062
854.5	1237	UZa	Core 90-22-854.5m	average gabbro								0.204
873.7	1218	UZa	Core 90-22-873.7m	average gabbro								0.210	1060
893.6	1198	UZa	Core 90-22-893.6m	average gabbro								0.217
903.8	1188	UZa	Core 90-22-903.8m	average gabbro								0.220	1064
914.2	1178	UZa	Core 90-22-914.2m	average gabbro								0.224	1056
941.8	1150	UZa	Core 90-22-941.8m	average gabbro								0.233	1066
458266	1131	MZ	Pukugagryggen	average gabbro	289	68	11.09	–31	40.44	554989	7564068	0.239	1068
458265	1098	MZ	Pukugagryggen	average gabbro	271	68	11.13	–31	40.48	554961	7564142	0.251	1064
458264	1060	MZ	Pukugagryggen	average gabbro	224	68	11.14	–31	40.52	554933	7564152	0.264	1071
458263	1055	MZ	Pukugagryggen	average gabbro	221	68	11.15	–31	40.59	554882	7564172	0.266	1064
458262	1053	MZ	Pukugagryggen	average gabbro	210	68	11.14	–31	40.63	554854	7564158	0.267	1073
458261	1032	MZ	Pukugagryggen	average gabbro	192	68	11.16	–31	40.65	554841	7564184	0.274	1070
458261a	1032	MZ	Pukugagryggen	average gabbro	192	68	11.16	–31	40.65	554841	7564184	0.274
458260	1024	MZ	Pukugagryggen	average gabbro	160	68	11.14	–31	40.78	554748	7564149	0.277	1073
458259	1010	MZ	Pukugagryggen	average gabbro	152	68	11.16	–31	40.80	554736	7564180	0.283	1075
458258	1009	MZ	Pukugagryggen	average gabbro	142	68	11.16	–31	40.85	554703	7564181	0.283	1073
458256	1003	MZ	Pukugagryggen	average gabbro	132	68	11.16	–31	40.87	554691	7564184	0.285	1078
458257	1003	MZ	Pukugagryggen	average gabbro	132	68	11.16	–31	40.87	554691	7564184	0.285	1075
458255	1002	MZ	Pukugagryggen	average gabbro	127	68	11.16	–31	40.89	554676	7564180	0.286	1075
458254	988	MZ	Pukugagryggen	average gabbro	117	68	11.18	–31	40.93	554647	7564219	0.291	1074
458253	984	MZ	Pukugagryggen	average gabbro	99	68	11.17	–31	41.01	554589	7564203	0.292	1079
458252	961	MZ	Pukugagryggen	average gabbro	84	68	11.19	–31	41.01	554591	7564233	0.301	1083
458251	953	MZ	Pukugagryggen	average gabbro	74	68	11.19	–31	41.11	554518	7564240	0.304	1076
458250	935	MZ	Pukugagryggen	average gabbro	63	68	11.21	–31	41.14	554497	7564283	0.311	1077
458249	930	MZ	Pukugagryggen	average gabbro	47	68	11.21	–31	41.18	554474	7564271	0.313	1081
458248	921	MZ	Pukugagryggen	average gabbro	36	68	11.22	–31	41.22	554446	7564293	0.316	1083
458247	920	MZ	Pukugagryggen	average gabbro	30	68	11.22	–31	41.24	554431	7564290	0.317	1065
458246	900	MZ	Pukugagryggen	average gabbro	1	68	11.24	–31	41.32	554370	7564323	0.325	1128
458289	890	MZ	Kræmer Ø	average gabbro	75	68	11.24	–31	42.82	553334	7564306	0.329	1080
458288	877	LZc	Kræmer Ø	average gabbro	74	68	11.26	–31	42.86	553309	7564345	0.334	1081
458287	875	LZc	Kræmer Ø	average gabbro	95	68	11.30	–31	42.89	553287	7564409	0.335	1093
458286	847	LZc	Kræmer Ø	average gabbro	86	68	11.33	–31	42.86	553308	7564468	0.346	1086
458285	830	LZc	Kræmer Ø	average gabbro	87	68	11.35	–31	42.88	553294	7564510	0.353	1087
458284	816	LZc	Kræmer Ø	average gabbro	85	68	11.37	–31	42.86	553306	7564538	0.358	1088
458283	808	LZc	Kræmer Ø	average gabbro	95	68	11.39	–31	42.88	553287	7564577	0.362	1086
458281	798	LZc	Kræmer Ø	average gabbro	94	68	11.40	–31	42.89	553280	7564597	0.366	1086
458282	798	LZc	Kræmer Ø	average gabbro	94	68	11.40	–31	42.89	553279	7564597	0.366	1082
458280	784	LZc	Kræmer Ø	average gabbro	95	68	11.42	–31	42.91	553270	7564634	0.372	1085
458279	752	LZc	Kræmer Ø	average gabbro	84	68	11.44	–31	42.94	553247	7564680	0.385	1090
458210	742	LZc	Uttental Plateau	average gabbro	700	68	12.82	–31	40.63	554787	7567276	0.390	1089
458209	723	LZc	Uttental Plateau	average gabbro	658	68	12.77	–31	40.74	554711	7567187	0.398	1099
458278	710	LZb	Kræmer Ø	average gabbro	59	68	11.46	–31	42.90	553272	7564720	0.403	1093
458208	703	LZb	Uttental Plateau	average gabbro	637	68	12.77	–31	40.78	554684	7567177	0.406	1100
458277	703	LZb	Kræmer Ø	average gabbro	59	68	11.47	–31	42.93	553252	7564730	0.406	1089
458207	681	LZb	Uttental Plateau	average gabbro	62	68	11.50	–31	42.93	553248	7564790	0.416	1094
458276	681	LZb	Kræmer Ø	average gabbro	592	68	12.72	–31	40.88	554618	7567090	0.416	1094
458206	634	LZb	Uttental Plateau	average gabbro	542	68	12.71	–31	41.00	554537	7567062	0.437	1099
458205	592	LZb	Uttental Plateau	average gabbro	498	68	12.70	–31	41.11	554462	7567036	0.456	1102
458204	580	LZb	Uttental Plateau	average gabbro	481	68	12.69	–31	41.14	554440	7567017	0.462	1109
458203	558	LZb	Uttental Plateau	average gabbro	453	68	12.67	–31	41.20	554400	7566989	0.472	1109
458202	519	LZb	Uttental Plateau	average gabbro	406	68	12.65	–31	41.32	554315	7566952	0.491	1100
458201	488	LZb	Uttental Plateau	average gabbro	363	68	12.63	–31	41.40	554261	7566913	0.506	1107
458233	447	LZb	Uttental Plateau	average gabbro	331	68	12.64	–31	41.50	554196	7566921	0.526	1112
458232	424	LZb	Uttental Plateau	average gabbro	308	68	12.64	–31	41.51	554185	7566923	0.537	1109
458231	367	LZb	Uttental Plateau	average gabbro	282	68	12.67	–31	41.65	554092	7566971	0.566	1107
458227	346	LZb	Uttental Plateau	average gabbro	266	68	12.67	–31	41.68	554070	7566978	0.576	1115
458226	294	LZb	Uttental Plateau	average gabbro	237	68	12.70	–31	41.74	554026	7567025	0.604	1121
458225	221	LZb	Uttental Plateau	average gabbro	155	68	12.67	–31	41.90	553916	7566984	0.643	1120
458224	177	LZb	Uttental Plateau	average gabbro	220	68	12.67	–31	42.13	553761	7566964	0.667	1124
458221	175	LZb	Uttental Plateau	average gabbro	246	68	12.65	–31	42.47	553526	7566931	0.668	1122
458220	173	LZa	Uttental Plateau	average gabbro	250	68	12.64	–31	42.60	553434	7566903	0.669	1126
458219	161	LZa	Uttental Plateau	average gabbro	261	68	12.66	–31	42.66	553390	7566941	0.676	1119
458218	159	LZa	Uttental Plateau	average gabbro	261	68	12.64	–31	42.81	553292	7566911	0.677	1111
458217	137	LZa	Uttental Plateau	average gabbro	258	68	12.66	–31	42.88	553239	7566940	0.689	1117
458216	125	LZa	Uttental Plateau	average gabbro	290	68	12.66	–31	43.03	553137	7566945	0.696	1119
458215	115	LZa	Uttental Plateau	average gabbro	287	68	12.66	–31	43.12	553077	7566942	0.701	1124
458214	107	LZa	Uttental Plateau	average gabbro	284	68	12.65	–31	43.21	553011	7566928	0.706	1129
458245	96	LZa	Uttental Plateau	average gabbro	275	68	12.65	–31	43.29	552960	7566918	0.712
458213	84	LZa	Uttental Plateau	average gabbro	273	68	12.65	–31	43.32	552935	7566924	0.719	1127
458212	54	LZa	Uttental Plateau	average gabbro	261	68	12.66	–31	43.39	552887	7566942	0.736	1119
458242	27	LZa	Uttental Plateau	average gabbro	250	68	12.67	–31	43.46	552841	7566954	0.752	1146
458211	7	LZa	Uttental Plateau	average gabbro	248	68	12.68	–31	43.52	552796	7566968	0.764	1124
a Names of samples from drill core 90-22 are the measured depth in metres. Samples with the prefix 4582 and 4586 are surface samples from the reference profile collected in 2000. b The baseline of stratigraphic height is the MBS–LZa boundary at Uttentals Plateau. c Altitute (m) estimated from altimeter and/or topographic map. d Latitude and longitude measured by GPS. e UTM coordinates calculated from latitude and longitude readings. f F is the mass fraction of magma remaining in the chamber calculated using equation (1) of Tegner et al. (2009). g Temperature (°C) calculated from average An content of plagioclase using the equation of Thy et al. (2013) (T (°C) = 895 + 3.8 * An (%) + 19 (°C).

Surface samples were collected in four sub-profiles for optimal stratigraphic continuity. In this way LZa, LZb, and LZc were collected on Uttental Plateau, LZc on Kraemer Ø, MZ along the north side of Forbindelsesgletscher, and UZc and SH on Basistoppen. The position of each surface sample was recorded by GPS and altimeter readings and plotted on a topographic map and aerial photos. The true stratigraphic distance between samples was established by correcting for the local dip of layering. A total of 85 gabbro surface samples were used in the construction of the combined reference profile.

The surface sample columns were combined with dip-corrected core logs for Hole 90-22 to construct a composite stratigraphic column that links the individual profiles and provides accurate locations of zone boundaries and thicknesses. The total stratigraphic section of the LS calculated in this way is 2165 m. The total number of samples used to construct the reference profile was 136 (85 surface and 51 drill core samples) giving an average sample interval of 16 m.

It is noteworthy that significant differences exist in the relative thicknesses of some zones and subzones compared to those given by Wager & Deer (1939). For example, our location of the LZ–MZ and MZ–UZ boundaries are stratigraphically higher and lower, respectively, resulting in a significantly reduced thickness for MZ relative to the stratigraphic column of Wager & Deer (1939). Likewise, we find that the relative thicknesses of LZc and UZa are greater than reported by Wager & Deer (1939). The present samples are collected essentially in the same profiles as those of Wager & Deer (1939). We therefore ascribe the differences in the thicknesses to improved positioning of samples and zone boundaries by GPS positioning and continuous drill core. A summary of the samples used are given in Table A2.2, listing the stratigraphic height in m of the reference profile together with the volume relations calculated by Tegner et al. (2009) and based on the volume relations of Nielsen (2004).

The field locations of the samples used by Wager & Deer (1939) and Wager & Brown (1967) are based on the detailed manuscript sample location map maintained by R.L. Wager at Oxford University, UK. The map is hand-drawn on two sheets of paper on which the topographic base map together with the main zone boundaries have been traced in pencil. The scale of the original map is identical to that used for the geological map in Wager & Brown (1967). A total of 4188 sample locations are include on two map sheets that are captioned ‘Working locality sheet / L.R.W.’ Wager’s manuscript locality maps are in the Wager Archives at Oxford University Museum of Natural History (M104); UK. Wager’s manuscript locality map is included in the Supplementary Files S5, in high-resolution PDF format.

The field locations of the samples used by McBirney (1989a) are available as manuscript locations on a copy of McBirney’s (1989b) printed geological map. This is now in the archives of the American Museum of Natural History (AMNH) and also included here as part of the Supplementary Files S5.

References

Appendix 3 Analytical methods

Sample preparation

Surface samples were selected without visible alteration and weighing 2–4 kg. A reference piece (0.5–1 kg) and a slab for thin section were cut from each sample. The reference pieces were stored in the collection of the Natural History Museum of Denmark (University of Copenhagen), for future studies. Weathered surfaces were removed with a diamond saw from the working sample. The remaining material was then crushed into <2 cm pellets in a hydraulic steel piston press and split into two portions, each of 30–40 g. These splits were grounded to c.10 mm fine powder in a corundum shatter box. The first split was ground for 3–5 min to pre-contaminate the shatter box and discharged. Hereafter, the shatter box was cleaned in ethanol and the second split was ground, also for 3–5 min to achieve the powder size that was then used for all geochemical analyses.

For the drill core samples, 10–16 cm long core sections were split along the long axis into pieces constituting, respectively, 1/3 and 2/3 by volume. The small reference split was stored at the Natural History Museum of Denmark (University of Copenhagen). A slab for thin section was cut from the upper end of the working split and the remaining material (200–500 g) was crushed into <2 cm aggregate in a steel-jaw crusher, followed by splitting and grinding in a tungsten-carbide shatter box.

X-ray fluorescence (XRF) analyses

LOI was determined by heating the powder in air in a muffle furnace at 950°C for 3 h. Fused glasses were prepared by mixing 0.75 g ignited powder with 3.75 g of Fluore-X65 HP (a commercial flux from Socachim Fine Chemicals consisting of 66 wt% Li₂B₄O₇ and 34 wt% LiBO₂) in a 30 ml 95Pt-5Au crucible. The crucible was transferred to a muffle furnace and the contents melted twice for 5 minutes at 1150°C, with swirling of the crucible between melting. After fusion, the melt was poured into a red-hot, 32 mm 95Pt-5Au mold and quenched with air to produce a flat glass disc. The glass disc was used for the major analysis.

Powder pellets were prepared by mixing thoroughly 6 g powder with 1.0 g phenol formaldehyde (British Bakelite Company; resin R0214). After mixing, the powder was placed in a die and pressed in a hydraulic press for 5 min at 30 tons. The pellet was placed in an oven operating at 110°C. After 30 min the phenol formaldehyde was set, and the pellet was ready for X-ray trace element analysis.

The major and the trace element analyses were performed on a PANalytical PW2400 X-ray spectrometer using SuperQ software. For the major elements a 3 kW Rh-tube was used operating at 50 kV and 55 mA along with PX-1 multilayer for Na and Mg, PE crystal for Al and Si, Ge crystal for P, LiF(200) crystal for K, Ca and Ti and LiF(220) crystal for Mn and Fe. The detector was a gas flow proportional counter using P10 gas (10% methane in Ar). For Mn and Fe, this detector was used in tandem with a sealed Xe detector.

For the trace elements Ba, La, Ce, V and Cr, the Rh tube was operated at 50 kV and 55 mA, for the rest of the trace elements the Rh tube was operated at 60 kV and 45 mA. LiF(200) crystal and 100m collimator were used throughout. The detector for Ba and La was a gas flow proportional counter, for V, Cr and Ce this counter was used in tandem with the sealed Xe counter. A scintillation counter was used for the rest of the trace elements.

A total of 44 international silicate rock reference materials, with compositions ranging from basaltic to rhyolitic, were used for the calibrations (Govindaraju 1994, 1995). For the major elements the fundamental parameter matrix correction model in the SuperQ software was used. For Ni, Cu, Zn, Rb, Sr, Y, Zr, Nb, Pb, Th, and U, the mass attenuation corrections are based on measuring the intensity of the Compton K_β line of Rh. For Ba, La, Ce, V, and Cr, determination of the major elements were included, and the FP matrix correction model was used. The analytical uncertainty was estimated by counting statistics as well as from the concurrent analyses of an internal reference standard (Appendix A3.1)

Appendix 3.1 Lower limit of detection, precision and accuracy of XRF analyses

	Counting statistics		East Greenland Basalt (GEUS 95358)
	1σ SD	LLD	Ave.	1 SD	Precision	Reference	Accuracy
			(n = 52)		(%RSD) a	value b	(%) c
Major elements (wt%)
SiO2	0.18	0.01	49.77	0.11	0.2	50.14	–0.7
TiO2	0.033		2.00	0.01	0.7	2.03	–1.3
Al2O3	0.18	0.01	14.39	0.04	0.2	14.67	–1.9
FeOtot	0.14	0.01	12.36	0.03	0.2	12.09	2.3
MnO	0.004	0.001	0.20	0.00	0.0	0.18	8.4
MgO	0.08	0.01	6.96	0.03	0.4	6.81	2.2
CaO	0.09	0.01	11.49	0.06	0.5	11.36	1.2
Na2O	0.05	0.01	2.38	0.06	2.5	2.27	4.7
K2O	0.01	0.01	0.25	0.00	1.6	0.26	–4.3
P2O5	0.08	0.01	0.19	0.00	0.7	0.19	–2.3
Total			99.99			100.00
Trace elements (ppm)
V	4		332	39	12	330	0.8
Cr	4	1	159	13	8	187	–14.9
Ni	1.2	0.6	78	8	10	83	–6.1
Cu	1.7	0.6	172	22	13	168	2.4
Zn	1.5	0.7	97	4	4	100	–3.1
Rb	0.2	0.6
Sr	2.6	0.5	206	3	1	205	0.3
Y	0.5	0.8	30	2	5	30	–0.2
Zr	3.1	0.5	114	2	2	113	0.3
Nb	0.2	0.6	8	1	15	8	–6.3
Ba	5	2	54	10	19	50	7.5
Pb	0.2	0.9
a %RSD calculated as 100 × (SD / Ave.). b Major elements from Geological Survey of Denmark and Greenland (L.M. Larsen personal communication 2002) and trace elements from Oregon State University (O. Stecher personal communication 2003). c Accuracy calculated as 100 × ([Ave. – reference] / reference). LLD: lower limit of detection.

FeO was determined by decomposing the sample in a Teflon crucible using a mixture of hydrofluoric and sulfuric acid at boiling point. The crucible and contents were plunged into boric acid solution. The ferrous iron liberated was titrated with potassium dichromate using barium diphenylamine sulfonate as indicator.

ICP-MS analyses

Transitional elements and REE were determined on whole-rock samples by ICP-MS at the Interdisciplinary Center of Plasma Mass Spectrometry at University of California, Davis. A portion of the homogenised powdered samples was dried in an oven overnight. Nearly 100 mg of each powder was weighed and placed in Savellex beakers with a HF:HNO₃ solution. This closed vessel digestion procedure follows the method by Jenner et al. (1990). The presence of refractory minerals in a few samples required microwave digestion.

An Agilent 7500 quadrapole ICP-MS was used with certified standards BIR-1, BHVO-1, BCR-2, and BE-N for constructing calibration curved. Drift was monitored by spiking each sample with an internal standard solution containing fixed concentrations of Cs, Ga, and In. Daily tuning ensured the highest sensitivity and lowest variability (%RSD > 3%) using a 10 ppb solution that contains Li, Cr, Y, Ce, and Tl. The production of ionised oxides (masses 156/140) and doubly charged ions (masses 70/140) were reduced to less than 1% and c. 2%, respectively. Precision and accuracy are evaluated based on multiple analyses of reference standards W-2 and BHVO-2 (Appendix A3.2).

Appendix 3.2 Precision and accuracy of ICP-MS analyses using the W-2 and BHVO-2 reference standards

Isotope	W-2					BHVO-2
	Ave. (ppm)	Precision	Accepted	Uncertainty	Accuracy (%) c	Ave. (ppm)	Precision	Accepted	Uncertainty	Accuracy (%) c
	(n = 6)	%RSD a	values (ppm) b	1σ SD		(n = 6)	%RSD a	values (ppm) b	1σ SD
45Sc	36.1	2.2	36	1.1	–0.3	32.5	2.7	32	13	–1.5
51V	270.5	2.7	260	12	–4.0	317.3	2.5	317	11	–0.1
52Cr	92.7	10.7	92	4.4	–0.7	291.7	4.4	280	19	–4.2
60Ni	65.0	6.1	70	2.5	7.1	114.2	4.4	119	7	4.0
59Co	42.8	6.3	43	2.1	0.5	44.8	3.9	45	3	0.4
68Zn	79.1	4.7	80	2	1.1	92.8	3.2	103	6	9.9
85Rb	21.3	3.0	21	1.1	–1.3	9.5	2.9	9.8	1	2.6
88Sr	201.1	5.1	190	3.0	–5.8	402.3	1.8	389	23	–3.4
89Y	23.7	4.8	23	1.6	–2.9	27.8	1.7	26	2	–7.0
90Zr	90.5	2.9	100	2	9.5	176.3	3.1	172	11	–2.5
93Nb	7.5	3.9	7.9		5.6	18.3	4.2	18	2	–1.7
138Ba	172.6	1.3	170	11	–1.3	130.3	1.7	130	13	–0.2
139La	10.6	1.5	10	0.59	–5.9	14.7	1.4	15	1	2.3
140Ce	23.1	1.6	23	1.5	–0.6	36.3	1.2	38	2	4.4
141Pr	3.0	1.9			0.0	5.2	1.3			0.0
146Nd	13.2	2.1	13	1	–1.4	24.0	1.8	25	1.8	4.0
147Sm	3.3	2.9	3.3	0.13	0.8	5.9	1.7	6.2	0.4	4.6
151Eu	1.1	3.4	1.0	0.06	–11.1	2.0	1.7			0.0
157Gd	3.7	3.4			0.0	5.9	2.4	6.3	0.2	7.1
159Tb	0.6	3.1	0.63		2.7	0.9	2.2	0.9		–0.5
163Dy	3.8	3.8	3.6	0.8	–5.4	5.2	1.5			0.0
165Ho	0.8	2.8			0.0	1.0	1.6	1.04	0.04	8.5
167Er	2.2	3.8	2.5		12.6	2.4	1.6			0.0
169Tm	0.3	6.0	0.38		12.2	0.3	4.4			0.0
174Yb	2.0	4.5	2.1	0.2	2.7	1.9	1.9	2.0	0.2	4.5
175Lu	0.3	4.5	0.33		7.9	0.3	2.6	0.28	0.01	4.6
178Hf	2.3	3.6	2.60	0.18	9.8	4.3	2.2	4.1	0.3	–4.7
184W	0.3	7.5			0.0	0.2	3.2			0.0
181Ta	0.5	9.0	0.5		9.8	1.2	6.3	1.4		16.4
208Pb	7.6	1.5	9.3		17.7	1.9	10.9			0.0
232Th	2.3	5.3	2.4	0.1	5.6	1.2	0.9	1.2	0.3	3.2
238U	0.5	5.4	0.53		–1.1	0.4	3.2
a %RSD calculated as 100 × (SD / Ave.). b Data source: http://minerals.cr.usgs.gov/geo_chem_stand/index.html Italic numbers are information values. c Accuracy calculated as 100 × ((Ave. – Accepted) / Accepted). W-2: USGS Geochemical Reference material W-2 (diabase). BHVO-2: USGS Geochemical Reference material (Hawaiian basalt).

Fluorine analyses

Fluorine was analysed using the ion selective electrode method of Stecher (1998). The precision is believed to be less than 3–6% with a lower limit of detection of 15 ppm. The accuracy was evaluated by Stecher (1983) to be within 5% of international reference rock samples.

Density determinations

The bulk-rock specific density of the surface and drill-core samples was determined by weighing the dry and clean samples in air and in water. The precision of the density measurements is estimated at ± 1–2%.

Electron microprobe analyses

Mineral compositions were determined at either University of California at Davis, USA, or at University of Aarhus, Denmark. The analyses at University of California at Davis were done using Cameca SX-50 or SX-100 electron microprobes with an acceleration voltage of 15 kV, a beam current of 10 nA, and counting times between 10 and 30 s. All mineral phases were analysed using natural minerals as standards for calibration and wavelength dispersive spectrometers. A beam diameter of 1–2 µm was used to analyse most minerals, except that pyroxenes were analysed with a 20–30 µm broad beam to minimise the effects of exsolution.

The analyses at the University of Aarhus were done with a JEOL 8600 Superprobe equipped with three wavelength dispersive spectrometers and one energy-dispersive spectrometer. Nearly all analyses were performed using a broad beam (c. 20 µm) operated at 20 kV and 10 nA current, using synthetic and natural standards for calibration and ZAF correction procedures. For pyroxenes, Si, Al, Fe, Mg, and Ca were measured by energy-dispersive spectrometry with a 200 s counting time, and Ti, Mn and, Na by wavelength dispersive spectrometry with a 40 s counting time. For olivine, Si, Fe, and Mg were measured by energy-dispersive spectrometry with a 120 s counting time and Mn and Ni were determined by wavelength dispersive spectrometry using a 40 s counting time. For plagioclase, Si, Al, Ca, and Na were determined by energy-dispersive spectrometry with a 120 s counting time, whereas Fe and K were determined by wavelength dispersive spectrometry with 40 s counting time.

When possible, a total of three points were analysed in the cores of each of three grains for each mineral (olivine, plagioclase, clinopyroxene, orthopyroxene, ilmenite, magnetite, apatite). The results are reported as averages and standard deviations for the specific thin section. Analyses with compositional anomalies, suggesting impurities, and with oxide sums lower than 98.5% or higher than 101.5% having generally been excluded from the average values. An internal pyroxene standard was analysed at both laboratories concurrently as a control and measure of analytical precision and accuracy (Appendix A3.3).

Appendix 3.3 Laboratory comparison of electron microprobe analyses (Batberg clinopyroxene)

	UCD		AU		Recommended
	Average	1σ SD	Average	1σ SD	(BB1989.286)
	(n = 35)		(n = 45)
SiO2	54.20	0.28	54.96	0.19	54.52
TiO2	0.11	0.02	0.10	0.02	0.09
Al2O3	0.38	0.03	0.31	0.02	0.27
FeO	1.34	0.07	1.29	0.09	1.13
MnO	0.03	0.02	0.03	0.02	0.03
MgO	17.74	0.17	17.38	0.18	17.68
CaO	24.53	0.24	24.73	0.17	24.21
Na2O	0.52	0.04	0.43	0.14	0.45
Cr2O3	0.67	0.05	0.63	0.05	(0.65)
Total	99.52		99.86		99.03
UCD: University of California at Davis, USA, Cameca microprobe. AU: University of Aarhus, Denmark, JEOL Superprobe. BB1989.286: recommended value by XRF on bulk Batberg clinopyroxene BB1989.286.

Least-squares mixing calculations

Modal proportions on a weight basis of the constituent minerals were calculated by weighted, least-squares, linear approximations (Bryan et al. 1969) using the mineral and the bulk-gabbro compositions. The weighting factors were 1.0 for all oxides, except for SiO₂ and Al₂O₃ which were assigned factors of 0.4 and 0.5, respectively. The following mineral phases were included in the calculations throughout the LS: olivine, plagioclase, clinopyroxene, orthopyroxene, ilmenite, magnetite, and apatite. Orthoclase and quarts were also included for the UZc. Only acceptable positive solutions to the least squares approximations were compiled with typical sums of the squares of the residuals below 0.10.

References