METHODS ARTICLE| SHORT

Long short-term memory networks enhance rainfall-runoff modelling at the national scale of Denmark

Julian Koch^*, Raphael Schneider

Department of Hydrology, Geological Survey of Denmark and Greenland, Copenhagen, Denmark

 

 

Abstract

This study explores the application of long short-term memory (LSTM) networks to simulate runoff at the national scale of Denmark using data from 301 catchments. This is the first LSTM application on Danish data. The results were benchmarked against the Danish national water resources model (DK-model), a physically based hydrological model. The median Kling-Gupta Efficiency (KGE), a common metric to assess performance of runoff predictions (optimum of 1), increased from 0.7 (DK-model) to 0.8 (LSTM) when trained against all catchments. Overall, the LSTM outperformed the DK-model in 80% of catchments. Despite the compelling KGE evaluation, the water balance closure was modelled less accurately by the LSTM. The applicability of LSTM networks for modelling ungauged catchments was assessed via a spatial split-sample experiment. A 20% spatial hold-out showed poorer performance of the LSTM with respect to the DK model. However, after pre-training, that is, weight initialisation obtained from training against simulated data from the DK-model, the performance of the LSTM was effectively improved. This formed a convincing argument supporting the knowledge-guided machine learning (ML) paradigm to integrate physically based models and ML to train robust models that generalise well.

Introduction

The runoff at a given point along a river network can be defined as the outflow generated in the upstream contributing area. Accurate modelling of runoff has been a prime research theme for several decades (Wagener et al. 2004). A multitude of numerical modelling tools, from parsimonious conceptual rainfall-runoff models to complex fully distributed physically based models (PBMs), have been developed. In recent years, machine learning (ML) models, in particular, long short-term memory (LSTM) networks, have proved useful for rainfall-runoff modelling. Since the first application by Kratzert et al. (2018), LSTMs quickly gained popularity and have typically outperformed traditional hydrological models under data-rich settings (Mai et al. 2021) and in ungauged catchments (Kratzert et al. 2019a).

The knowledge-guided ML paradigm aims to increase robustness and generalisability by integrating scientific knowledge into ML models (Nearing et al. 2020; Reichstein et al. 2019). This can be achieved by building physical constraints, such as the first-principle law of mass conservation (Hoedt et al. 2021), into a ML model or using a PBM to augment training data (Jia et al. 2021). In this context, the method of pre-training by weight initialisation using PBM simulation data appears to be very promising, as a pre-trained LSTM attempts to emulate a PBM.

The rapid advancement of ML models for runoff prediction was facilitated by the availability of multiple large-scale runoff data sets containing a long timeseries of observed runoff, dynamic meteorological forcing and static catchment attributes, referred to as catchment attributes and meteorology for large-sample studies (CAMELS) data sets (e.g. Addor et al. 2017). In this article, we highlight the value of Danish hydrological big data for the advancement of ML-based runoff modelling. The Danish case offers a data-rich setting with over 300 stations and high-quality auxiliary data. Moreover, there exists a national water resources model (the DK-model), an advanced hydrological PBM that integrates groundwater and surface water processes (Højberg et al. 2013; Stisen et al. 2019). The DK-model is a perfect benchmark for ML model development and provides simulated runoff, which is valuable for augmentation, as well as auxiliary hydrological information, such as groundwater conditions.

In this study, we aim to (1) highlight the value of Danish hydrological big data for advancing ML research at an international level, (2) implement a state-of-the-art LSTM to model runoff at the national scale of Denmark and (3) test a knowledge-guided LSTM based upon pre-training against simulated runoff obtained from a PBM.

Methods

Data

As in existing CAMELS data sets, we curated a data set comprising observed runoff as well as dynamic and static attributes for 301 Danish catchments (Fig. 1). The catchments vary in size between 10 km² and 2574 km² with an average of 133 km². The dynamic variables cover a period of 21 years (1990–2011) at daily timesteps and comprise observed runoff, simulated runoff (DK-model), air temperature, potential evapotranspiration and precipitation (Fig. 2). The three meteorological variables were derived from gridded data provided by the Danish Meteorological Institute and represent daily-averaged conditions for the entire catchment (Scharling 1999a, 1999b). A complete timeseries of 21 years of daily observed runoff were available for 51% of the catchments, with 77% of the catchments having at least an 80% coverage. The runoff was normalised by the catchment size to mm/day to give equal weight to the catchments during training, independent of their size. In total, 17 static catchment attributes were compiled. Eleven of which were calculated as catchment averages: precipitation, potential evapotranspiration, air temperature, slope, topographic wetness index, clay fraction, annual, summer and winter-simulated water table depth (DK-model), exceedance probability of a simulated water-table depth less than 1 m (DK-model) and the thickness of the surficial clay layer. Five land-use classes were expressed as percentages: forest, wetland, lake, agriculture and urban. Finally, the catchment area was included as well. All data are available at https://doi.org/10.22008/FK2/YCQXTR.

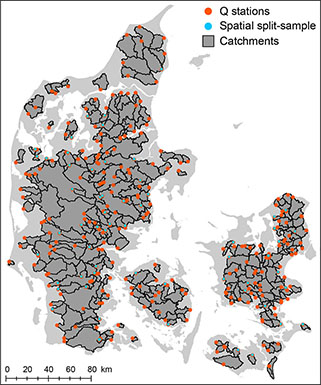
Fig. 1 Map of Denmark showing the 301 catchments used in this study. 60 catchments were randomly sampled for the spatio-temporal split-sample experiment.

 

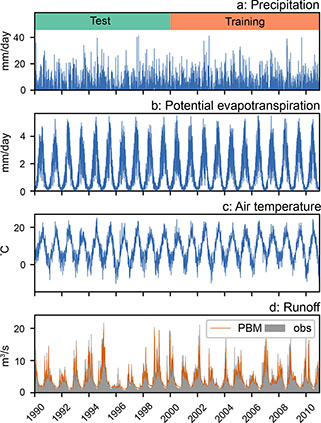
Fig. 2 Dynamic input data for a single catchment used to train the LSTM. a: Precipitation. b: Potential evapotranspiration. c: Air temperature. d: Observed runoff (obs) and simulated runoff (PBM) were used as training data. The training period and test period are shown in a.

Long short-term memory

The LSTM network architecture is a special type of recurrent neural network, designed to store and regulate information over time, which makes LSTMs well suited to learn long-term dependencies and memory effects (Hochreiter & Schmidhuber 1997). The LSTM is described in full elsewhere (Kratzert et al. 2018; Shen 2018). Similar to traditional hydrological models, the LSTM processes input data time step after time step. Runoff on a specific day is simulated based on the timeseries of length n of the preceding n days of meteorological data. Kratzert et al. (2019b) developed the entity-aware LSTM, which is an adaptation of the standard LSTM capable of learning catchment similarities based on the static attributes, which are treated in a separate embedding layer. In this study, we applied the proposed entity-aware LSTM, referred to simply as LSTM hereafter. We used the NeuralHydrology codebase (github.com/neuralhydrology/neuralhydrology/) to train and evaluate the models used in this study.

Experimental setup

Hyperparameters and general settings

As the purpose of this study was to initially explore the LSTM applicability, hyperparameters were not optimised. Following Kratzert et al. (2019b), we assigned the following hyperparameter values: a learning rate of 0.001, a batch size of 256, an input length of 270 days, 64 hidden cell states, a dropout rate of 0.4 and 20 training epochs. All models were trained with five different seeds and the average of the five models was used for the final LSTM prediction. The model setup files are available at https://doi.org/10.22008/FK2/YCQXTR.

Split-sample experiments

We conducted both a temporal split-sample and a spatio-temporal split-sample experiment to test the capabilities of a LSTM for Danish runoff data. The temporal split-sample experiment used data from all 301 stations for training. The timeseries were split into a training period of 11 years (2000–2011) and a test period of 10 years (1990–1999; Fig. 2). The two periods correspond to the calibration and test period of the DK-model, which permitted a fair comparison between the two models. The spatio-temporal split-sample experiment was divided into the same training and test periods. Furthermore, 20% of the stations were randomly selected and removed from the training data set and retained for model evaluation of the spatio-temporal split-sample experiment (i.e. a 20% spatial hold-out; Fig. 1). This experiment offers a more robust evaluation, as it tests the transferability of 80% of stations to the remaining 20%. This allows us to assess the ability to predict ungauged basins.

Pre-training

The concept of pre-training can be used to initialise the weights of a LSTM using alternative runoff data before fine-tuning the LSTM using the actual runoff data from the catchments of interest. Runoff data for pre-training can potentially be obtained from observational data sets from a larger or different geographical region or from a PBM. In this study, we followed the latter and employed simulation data from the DK-model to pre-train. In this way, the LSTM aimed to emulate the process descriptions of the PBM before being fine-tuned against observed runoff. The training epochs were set to 15 for pre-training and 5 for fine-tuning. Simulated runoff at all 301 stations for the training period of 11 years (2000–2011) was used for pre-training, and it was applied to both split-sample experiments.

Evaluation metrics

For training the LSTM network, the mean squared error (MSE) between the observed and simulated runoff was selected as the loss function. Two alternative metrics were calculated for the model evaluation, namely the Kling-Gupta Efficiency (KGE) and the averaged flow balance (Fbal). KGE is a three-component metric that considers the correlation, the standard deviation ratio and the bias between the observed and simulated runoff (Gupta et al. 2009). Fbal quantifies the water balance closure between the observed and simulated runoff relative to the observed flow (Henriksen et al. 2003). Negative Fbal scores indicate an overestimation of the model with respect to the observed runoff. The optimal values for KGE and Fbal are 1 and 0, respectively.

Results and discussions

The cumulative density functions for KGE and Fbal are presented in Figure 3. The LSTM was benchmarked against the DK-model (PBM), and the effect of pre-training was also investigated. Superior performance could be attributed to the LSTM, with and without pre-training, with respect to KGE for the temporal split-sample experiment. The median KGE was 0.8 for both LSTM configurations and 0.7 for the PBM. The conclusion was less clear for the water balance closure (Fbal); here, the PBM showed normally distributed under- and over-estimates with a median close to zero. However, the LSTMs were skewed towards negative values, that is, overestimation of runoff, with a median of –0.08. Overestimated runoff was predominately evident during the low-flow summer periods. Using alternative loss functions instead of the MSE in the LSTM training may alleviate this problem.

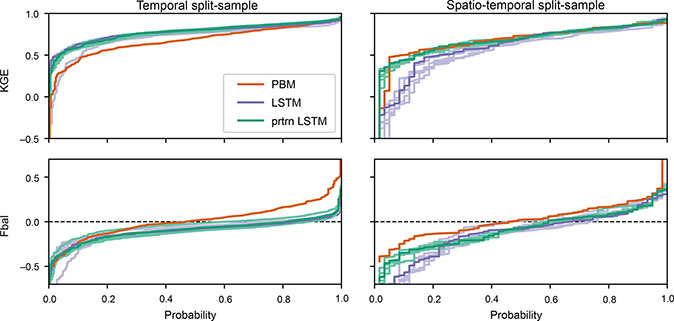
Fig. 3 Cumulative density functions for KGE and Fbal in the test period for runoff simulated by the DK-model (PBM), the LSTM model and the pre-trained LSTM model (prtrn LSTM). The temporal split-sample experiment is depicted in the left panels and the spatio-temporal split-sample experiment in the right panels. The optimal value of Fbal is highlighted with a dashed horizontal line. The LSTM predictions are based on the mean of 5 seeds, indicated here with transparent coloured lines.

The spatio-temporal split-sample experiment revealed that the LSTM did not generalise well to ungauged basins. The median KGE was 0.69 and comparable with the PBM (KGE = 0.73), despite poor KGE scores for the lowest 20% of the cumulative density function. The same was evident for Fbal, where the lowest 20% performed poorly with respect to the PBM. However, pre-training using PBM data resulted in better performance for ungauged basins, making them comparable with the PBM. This emphasised the merit of pre-training. For the spatio-temporal split-sample experiment, where information was evidently missing in the training data set, pre-training against PBM data helped to increase performance. However, the performance did not change for the temporal split-sample experiment, where the observations provided enough information.

Considering KGE for the temporal split-sample experiment, the LSTM outperformed the PBM in 80% of catchments. This fell to 44% for the spatio-temporal experiment but could rise to 54% through pre-training. Considering the absolute Fbal, 68% of the catchments were simulated more precisely by the LSTM than by the PBM for the temporal split-sample experiment. For the spatio-temporal split-sample experiment, this could be raised slightly from 44% to 49% through pre-training.

The simulation results for two selected catchments for the 10-year test period of the temporal and spatio-temporal split-sample experiments are presented in Figure 4. In the first catchment (260080), the performance between the LSTMs and the PBM was very comparable with a KGE score of 0.8 (PBM) and 0.78 (LSTM) for the temporal split-sample experiment. The performance dropped to 0.66 in the spatio-temporal split-sample experiment but increased to 0.8 through pre-training. The second catchment (420022) showed a very poor performance for the spatio-temporal split-sample experiment (KGE = –0.12). However, KGE improved to 0.78 through pre-training and thus became comparable with the PBM (KGE = 0.75). In other words, the spatio-temporal split-sample experiment for catchment 260 080 could be simulated accurately without pre-training, because the LSTM could learn the runoff behaviour of that catchment using data from similar neighbouring or upstream catchments. However, the runoff behaviour of catchment 420022 could not be learned without data from the same catchment. Nevertheless, pre-training using PBM data helped to increase the performance of the LSTM. Figure 4 presents results for a large (260080, 323 km²) and a small (420022, 44 km²) catchment. Smaller catchments generally perform less well due to the stronger imprint of anthropogenic activities (drainage and abstraction) and an increased uncertainty of precipitation data for smaller catchments.

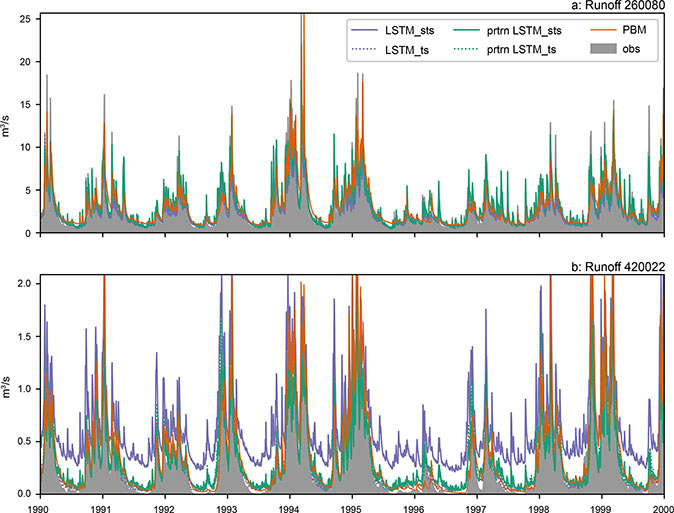
Fig. 4 Two example catchments showing the observed (obs) and simulated runoff for the test period. a: Catchment 260080, 323 km². b: Catchment 420022, 44 km². Simulated data comprise the DK-model (PBM), the LSTM-based model and the pre-trained LSTM-based model (prtrn LSTM). The runoff predictions of the LSTM-based models are given for the temporal split-sample (ts) and spatio-temporal split-sample (sts) experiments.

The superior performance of LSTMs over conceptual rainfall-runoff models or hydrological PBMs was demonstrated for temporal split-sample experiments by Kratzert et al. (2018), Gauch et al. (2021), Mai et al. (2021) and others; however, conclusions of the spatial transferability to ungauged basins are disputed. Kratzert et al. (2019a) reported a superior performance of LSTM for a small spatial hold-out (8%), whereas Mai et al. (2021) found a worse performance for a more systematic spatial hold-out.

Loss function plots are presented in Supplementary file S1 to elucidate the training of the applied modelling experiments in more detail. The data generally support the chosen hyperparameter values and number of training epochs.

To our knowledge, this is the first study that demonstrates the merits of pre-training against PBM simulation data for runoff modelling in the context of knowledge-guided ML. In a related study, pre-training using PBM data was found to be beneficial for the modelling of lake-water temperature (Read et al. 2019). For rainfall-runoff modelling, pre-training has so far been found to be suitable for transferring trained LSTMs from one geographical region to another (Ma et al. 2021). We have shown that pre-training using PBM data offers great potential to initialise the LSTM with diverse runoff behaviour. Here, we constrained only the pre-training to the same catchments and time; however, in theory, PBM simulations for different climate change scenarios or a larger geographical domain could inform the LSTM with diverse runoff behaviour not seen in the observed runoff data.

Most of the published studies on LSTM runoff modelling are of catchments with a low anthropogenic impact; however, recent efforts to model highly managed catchments have documented promising results as well (Ouyang et al. 2021). The 301 Danish catchments selected in this study are, to a large degree, affected by groundwater abstraction and drainage, and the effect of the degree of anthropogenic impact on model performance and transferability should be investigated in future work.

Conclusions

We draw the following main conclusions from the initial application of LSTM networks for rainfall runoff modelling at the national scale of Denmark:

Danish hydrological big data have the potential for conducting ML research at an international level. The DK-model serves as a valuable benchmark as well as a source for augmented training data and input data in the form of static catchment attributes.

An LSTM can outperform a state-of-the-art hydrological model; however, accuracy decreases for ungauged catchments. This can be alleviated by pre-training against physically based simulated runoff, providing crucial information to the LSTM where needed.

Future research studies should (1) advance knowledge-guided ML to use hydrological knowledge provided by the DK-model optimally; (2) test alternative LSTM architectures, hyperparameters and loss functions; (3) study the effect of anthropogenic impact (drainage and groundwater abstraction) on the LSTM; (4) investigate ways of interpreting LSTM models to gain new insights into the runoff process in Denmark; (5) apply a broad range of hydrological signatures in the evaluation of LSTMs; and (6) produce a CAMELS data set for Denmark to provide high-quality hydrological and meteorological data.

Acknowledgements

The authors acknowledge the developer team behind the NeuralHydrology codebase for making LSTM modelling tools so accessible. Furthermore, GEUS colleagues H.J. Henriksen and S. Stisen are thanked for providing valuable feedback to this manuscript. Two anonymous reviewers are thanked for providing valuable comments to this manuscript.

Author contributions

JK: code development, writing original draft and visualisation. RS: data preparation. Both authors have conceptualised the study and design, read, edited and agreed to the published version of the manuscript.

Additional files

All data and model setups are available at: https://doi.org/10.22008/FK2/YCQXTR. An additional supplementary file is available at: https://doi.org/10.22008/FK2/WCF76I.

References

Addor, N., Newman, A.J., Mizukami, N. & Clark, M.P. 2017: The CAMELS data set: Catchment attributes and meteorology for large-sample studies. Hydrology and Earth System Sciences 21, 5293–5313. https://doi.org/10.5194/hess-21-5293-2017

Gauch, M., Mai, J. & Lin, J. 2021: The proper care and feeding of CAMELS: How limited training data affects streamflow prediction. Environmental Modelling and Software 135, 104926. https://doi.org/10.1016/j.envsoft.2020.104926

Gupta, H.V, Kling, H., Yilmaz, K.K. & Martinez, G.F. 2009: Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling. Journal of Hydrology 377(1–2), 80–91. https://doi.org/10.1016/j.jhydrol.2009.08.003

Henriksen, H.J., Troldborg, L., Nyegaard, P., Sonnenborg, T.O., Refsgaard, J.C. & Madsen, B. 2003: Methodology for construction, calibration and validation of a national hydrological model for Denmark. Journal of Hydrology 280, 52–71. https://doi.org/10.1016/S0022-1694(03)00186-0

Hochreiter, S. & Schmidhuber, J. 1997: Long Short-Term Memory. Neural Computation 9, 1735–1780. https://doi.org/10.1162/neco.1997.9.8.1735

Hoedt, P.-J., Kratzert, F., Klotz, D., Halmich, C., Holzleitner, M., Nearing, G., Hochreiter, S. & Klambauer, G. 2021: MC-LSTM: Mass-Conserving LSTM. arXiv preprint arXiv:2101.05186 (2021).

Højberg, A.L., Troldborg, L., Stisen, S., Christensen, B.B.S. & Henriksen, H.J. 2013: Stakeholder driven update and improvement of a national water resources model. Environmental Modelling and Software 40, 202–213. https://doi.org/10.1016/j.envsoft.2012.09.010

Jia, X. et al. 2021: Physics-guided recurrent graph model for predicting flow and temperature in river networks. In: Demeniconi, C. & Davidson, I. (eds): Proceedings of the 2021 SIAM International Conference on Data Mining (SDM), Virtual conference, 612–620. https://doi.org/10.1137/1.9781611976700.69

Kratzert, F., Klotz, D., Brenner, C., Schulz, K. & Herrnegger, M. 2018: Rainfall-runoff modelling using Long Short-Term Memory (LSTM) networks. Hydrology and Earth System Sciences 22, 6005–6022. https://doi.org/10.5194/hess-22-6005-2018

Kratzert, F., Klotz, D., Herrnegger, M., Sampson, A.K., Hochreiter, S. & Nearing, G.S. 2019a: Toward improved predictions in ungauged basins: Exploiting the power of machine learning. Water Resources Research 55, 11344–11354. https://doi.org/10.1029/2019WR026065

Kratzert, F., Klotz, D., Shalev, G., Klambauer, G., Hochreiter, S. & Nearing, G. 2019b: Towards learning universal, regional, and local hydrological behaviors via machine learning applied to large-sample datasets. Hydrology and Earth System Sciences 23, 5089–5110. https://doi.org/10.5194/hess-23-5089-2019

Ma, K. et al. 2021: Transferring hydrologic data across continents – Leveraging data-rich regions to improve hydrologic prediction in data-sparse regions. Water Resources Research 57, e2020WR028600. https://doi.org/10.1029/2020WR028600

Mai, J. et al. 2021: Great lakes runoff intercomparison project phase 3: Lake Erie (GRIP-E). Journal of Hydrologic Engineering 26, 1–19. https://doi.org/10.1061/(asce)he.1943-5584.0002097

Nearing, G.S., Kratzert, F., Sampson, A.K., Pelissier, C.S., Klotz, D., Frame, J.M., Prieto, C. & Gupta, H.V. 2020: What role does hydrological science play in the age of machine learning? Water Resources Research 57, e2020WR028091. https://doi.org/10.1029/2020wr028091

Ouyang, W., Lawson, K., Feng, D., Ye, L., Zhang, C. & Shen, C. 2021: Continental-scale streamflow modeling of basins with reservoirs: Towards a coherent deep-learning-based strategy. Journal of Hydrology 599, 126455. https://doi.org/10.1016/j.jhydrol.2021.126455

Read, J.S. et al. 2019: Process-guided deep learning predictions of lake water temperature. Water Resources Research 55, 9173–9190. https://doi.org/10.1029/2019WR024922

Reichstein, M., Camps-Valls, G., Stevens, B., Jung, M., Denzler, J., Carvalhais, N. & Prabhat 2019: Deep learning and process understanding for data-driven Earth system science. Nature 566(7743), 195–204. https://doi.org/10.1038/s41586-019-0912-1

Scharling, M. 1999a: Klimagrid Danmark: Nedbør, lufttemperatur og potentiel fordampning 20*20 & 40*40 km. Danish Meteorological Institute Technical Report 99-12, DMI, Copenhagen, DK.

Scharling, M. 1999b: Klimagrid Danmark: Nedbør 10*10 km (ver. 2). Danish Meteorological Institute Technical Report 99-15, DMI, Copenhagen, DK.

Shen, C. 2018: A trans-disciplinary review of deep learning research and its relevance for water resources scientists. Water Resources Research 54, 8558–8593. https://doi.org/10.1029/2018WR022643

Stisen, S., Ondracek, M., Troldborg, L., Schneider, R.J.M. & van Thil, M.J. 2019: National vandressource model. Modelopstilling og kalibrering af DK-model 2019. Danmarks og Grønlands Geologiske Undersøgelse Rapport 2019/31, GEUS, Copenhagen, DK.

Wagener, T., Wheater, H.S. & Gupta, H.V. 2004: Rainfall-runoff modelling in gauged and ungauged catchments, 332 pp. London: Imperial College Press. https://doi.org/10.1142/p335